13.2三角形全等的条件1[上学期]
文档属性
| 名称 | 13.2三角形全等的条件1[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 201.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-15 23:45:00 | ||
图片预览







文档简介
课件27张PPT。13.2三角形全等的条件(1)学习目标
1、通过动手实践,自主探索掌握三角形全等的条件一,了解三角形的稳定性。
2、结合图形能准确表述三角形全等的判定方法一“边边边”,为证明线段相等或角相等创造条件。
会利用“边边边”公理判定三角形全等。自学指导
1、对应边相等,对应角相等的两个三角形全等。全等的条件能否减少一些?可减少哪些呢?
2、一个条件,两个条件,三个条件可以吗?
3、三条边对应相等两个三角形全等吗?
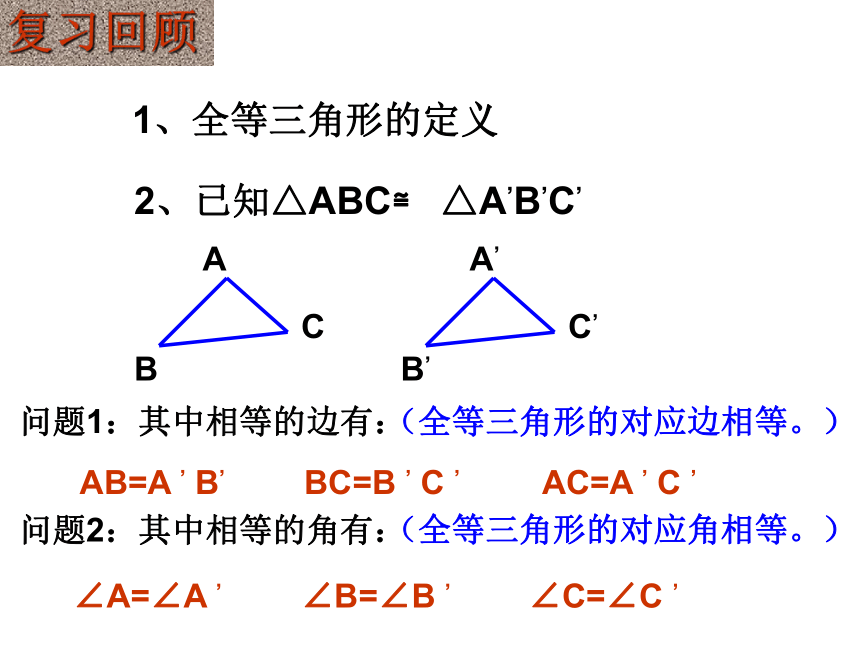
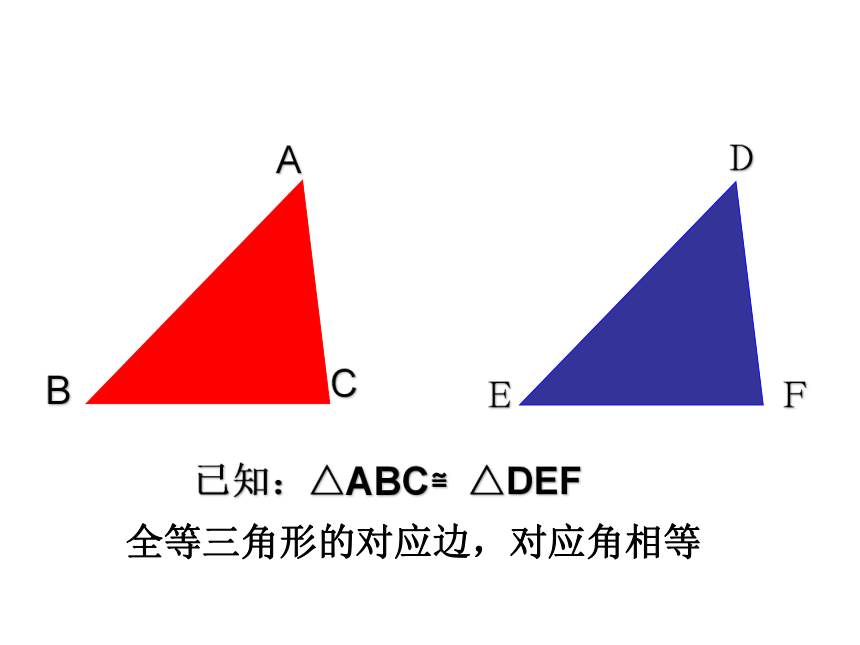
4、证明两个三角形全等的书写步骤是什么?复习回顾1、全等三角形的定义2、已知△ABC≌ △A’B’C’问题1:其中相等的边有:问题2:其中相等的角有:AB=A ’ B’BC=B ’ C ’AC=A ’ C ’∠A=∠A ’∠B=∠B ’∠C=∠C ’(全等三角形的对应边相等。)(全等三角形的对应角相等。)ABC已知:△ABC≌△DEF全等三角形的对应边,对应角相等问题引入:
小颖作业本上画的三角形被墨迹污染了,她想画一个与原来完全一样的三角形,她该怎么办?请你帮助小颖想一个办法,并说明你的理由?注意:与原来完全一样的三角形,即是与原来三角形全等的三角形。想一想:
要画一个三角形与小颖画的三角形全等。需要几个与边或角的大小有关的条件?只知道一个条件(一角或一边)行吗?两个条件呢?三个条件呢?让我们一起来探索三角形全等的条件探究1:
先任意画出一个△ABC,再画一个△ A’B’C’,使△ABC满足上述六个条件中的一个或两个,你画出的△ABC与△ A’B’C’全等吗?做一做 1.已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
(不一定全等) 2.已知一个三角形的三条边分别为4cm,5cm,7cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?做一做:
(1)只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?1)三角形的一个内角为30°,一条边为3cm;
2) 三角形的两个内角分别为30°和45°;
3)三角形的两条边分别为4cm和6cm.按下面的条件画三角形,画完后小组内交流,看所画的三角形是否全等。(其它条件不确定)(2)给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?三角形的一个内角为30 ,一条边为3cm30?给出两个条件时, 所画的三角形一定全等吗?给出两个条件时, 所画的三角形一定全等吗?如果三角形的两个内角分别是30 ,50 时30?30?50?50?给出两个条件时, 所画的三角形一定全等吗?如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm只给两个条件作出三角形,不能保正所画出的三角形一定全等。?探究一 ? 1.给定一个条件:(1)一条边(2)一个角 失 败2.给定两个条件:(1)两边(2)一边一角(3)两角 失 败探究2:
先任意画出一个△ABC,再画出一个△ A’B‘C’,使A’B‘=AB,B’C‘=BC,C’A‘=CA,把画好的△ A‘B’C‘剪下,放到△ ABC上,它们全等吗?△ABC≌ △A’B’C’由此得出定理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。 应用举例? 例1:如图所示,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。
求证:△ABD≌△ACD。证明:∵D是BC的中点∴BD=CD在△ABD和△ACD中AB=ACBD=CDAD=AD∴△ABD≌△ACD(SSS)像上述判断两个三角形全等的推理过程,
叫做证明三角形全等。已知如图所示,AC=FE,BC=DE,AD=FB,要用“边边边”证明△ABC≌△FDE,需要那些条件?如何证明??思考 ? △ABC≌△DEF在△ABC和△DEF中练一练 ? 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?试一试:1.如图,AD=BC,AC=BD,
求证(1)∠DAB= ∠CBA
(2)∠ACD= ∠BDC2.如图,AB=CD,AE=DF,CE=BF,
求证:AE∥DF练一练: 如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。
求证:∠A=∠D。做一做: 如图,已知AB=CD,BC=DA.你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么? DBAC解:在△ABC与△CDA中,
∵∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等) ∴AB∥CD,AD∥BC(内错角相等,两直线平行)探究:如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中 ∵BD=CD,BH=CH,DH=DH∴△DBH≌△DCH(SSS) 小结:
今天我们经历了画图验证两个三角形全等的过程,探索出两个三角形全等的条件之一“三边对应相等的两个三角形全等”,我们可以利用它来判别两个三角形是否全等。
1、通过动手实践,自主探索掌握三角形全等的条件一,了解三角形的稳定性。
2、结合图形能准确表述三角形全等的判定方法一“边边边”,为证明线段相等或角相等创造条件。
会利用“边边边”公理判定三角形全等。自学指导
1、对应边相等,对应角相等的两个三角形全等。全等的条件能否减少一些?可减少哪些呢?
2、一个条件,两个条件,三个条件可以吗?
3、三条边对应相等两个三角形全等吗?
4、证明两个三角形全等的书写步骤是什么?复习回顾1、全等三角形的定义2、已知△ABC≌ △A’B’C’问题1:其中相等的边有:问题2:其中相等的角有:AB=A ’ B’BC=B ’ C ’AC=A ’ C ’∠A=∠A ’∠B=∠B ’∠C=∠C ’(全等三角形的对应边相等。)(全等三角形的对应角相等。)ABC已知:△ABC≌△DEF全等三角形的对应边,对应角相等问题引入:
小颖作业本上画的三角形被墨迹污染了,她想画一个与原来完全一样的三角形,她该怎么办?请你帮助小颖想一个办法,并说明你的理由?注意:与原来完全一样的三角形,即是与原来三角形全等的三角形。想一想:
要画一个三角形与小颖画的三角形全等。需要几个与边或角的大小有关的条件?只知道一个条件(一角或一边)行吗?两个条件呢?三个条件呢?让我们一起来探索三角形全等的条件探究1:
先任意画出一个△ABC,再画一个△ A’B’C’,使△ABC满足上述六个条件中的一个或两个,你画出的△ABC与△ A’B’C’全等吗?做一做 1.已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
(不一定全等) 2.已知一个三角形的三条边分别为4cm,5cm,7cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?做一做:
(1)只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?1)三角形的一个内角为30°,一条边为3cm;
2) 三角形的两个内角分别为30°和45°;
3)三角形的两条边分别为4cm和6cm.按下面的条件画三角形,画完后小组内交流,看所画的三角形是否全等。(其它条件不确定)(2)给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?三角形的一个内角为30 ,一条边为3cm30?给出两个条件时, 所画的三角形一定全等吗?给出两个条件时, 所画的三角形一定全等吗?如果三角形的两个内角分别是30 ,50 时30?30?50?50?给出两个条件时, 所画的三角形一定全等吗?如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm只给两个条件作出三角形,不能保正所画出的三角形一定全等。?探究一 ? 1.给定一个条件:(1)一条边(2)一个角 失 败2.给定两个条件:(1)两边(2)一边一角(3)两角 失 败探究2:
先任意画出一个△ABC,再画出一个△ A’B‘C’,使A’B‘=AB,B’C‘=BC,C’A‘=CA,把画好的△ A‘B’C‘剪下,放到△ ABC上,它们全等吗?△ABC≌ △A’B’C’由此得出定理:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”这个定理说明,只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这也是三角形具有稳定性的原理。 应用举例? 例1:如图所示,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。
求证:△ABD≌△ACD。证明:∵D是BC的中点∴BD=CD在△ABD和△ACD中AB=ACBD=CDAD=AD∴△ABD≌△ACD(SSS)像上述判断两个三角形全等的推理过程,
叫做证明三角形全等。已知如图所示,AC=FE,BC=DE,AD=FB,要用“边边边”证明△ABC≌△FDE,需要那些条件?如何证明??思考 ? △ABC≌△DEF在△ABC和△DEF中练一练 ? 工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?试一试:1.如图,AD=BC,AC=BD,
求证(1)∠DAB= ∠CBA
(2)∠ACD= ∠BDC2.如图,AB=CD,AE=DF,CE=BF,
求证:AE∥DF练一练: 如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。
求证:∠A=∠D。做一做: 如图,已知AB=CD,BC=DA.你能说明△ABC与△CDA全等吗?你能说明AB∥CD,AD∥BC吗?为什么? DBAC解:在△ABC与△CDA中,
∵∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形对应角相等) ∴AB∥CD,AD∥BC(内错角相等,两直线平行)探究:如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中 ∵BD=CD,BH=CH,DH=DH∴△DBH≌△DCH(SSS) 小结:
今天我们经历了画图验证两个三角形全等的过程,探索出两个三角形全等的条件之一“三边对应相等的两个三角形全等”,我们可以利用它来判别两个三角形是否全等。
