13.2三角形全等的条件2.[上学期]
文档属性
| 名称 | 13.2三角形全等的条件2.[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-15 00:00:00 | ||
图片预览



文档简介
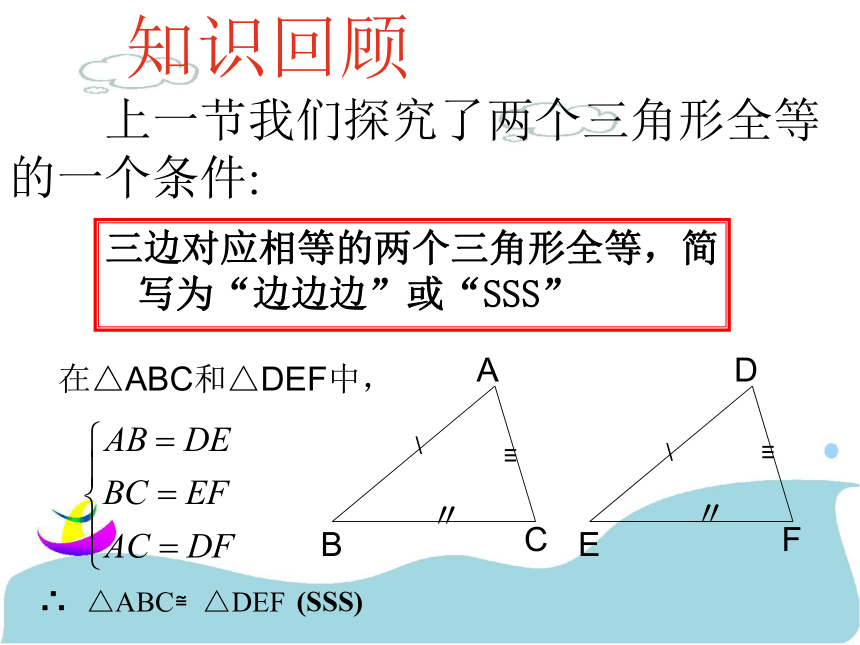
课件35张PPT。三角形全等的条件(2)三边对应相等的两个三角形全等,简写为“边边边”或“SSS”在△ABC和△DEF中,△ABC≌△DEF∴(SSS) 上一节我们探究了两个三角形全等的一个条件:知识回顾 1、在括号内填写适当的理由:如图,已知AB=DC,AC=DB,那么∠A=∠D.说明理由.∵AB=DC( )AC=DB( )BC=CB( )∴△ABC≌△DCB( )∴∠A=∠D已知已知公共边SSS(全等三角形的对应角相等)除了SSS外,还有其他情况吗?今天我们继续探索三角形全等的条件.思考(2) 三条边(1) 三个角(3) 两边一角(4) 两角一边 当两个三角形满足六个条件中的三个时,有四种情况:SSS不能!?活动1:
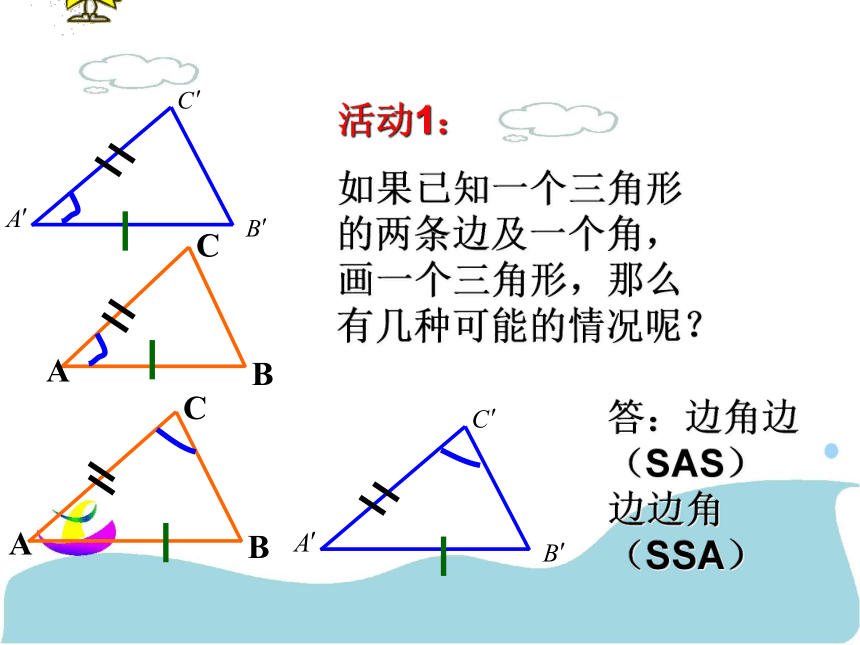
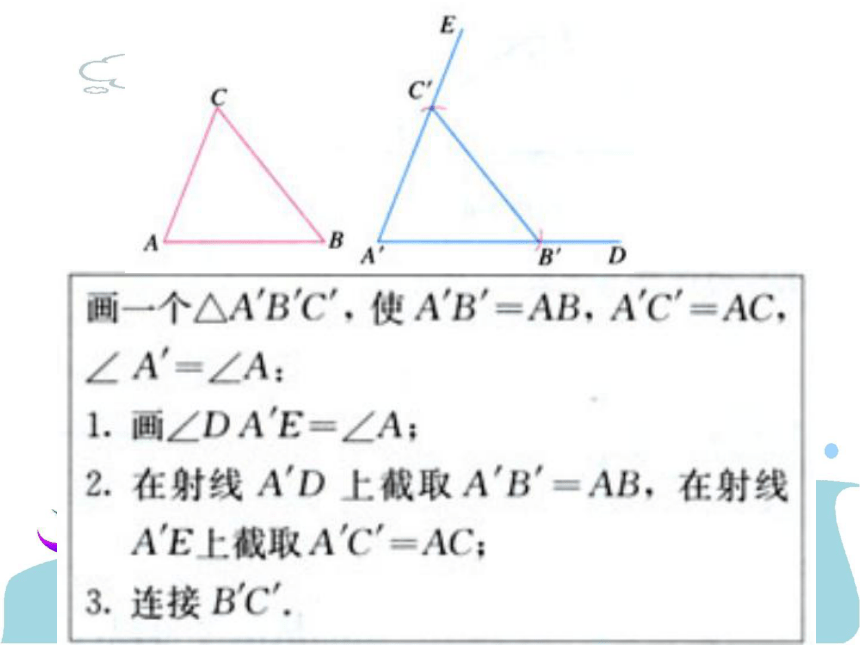
如果已知一个三角形的两条边及一个角,画一个三角形,那么有几种可能的情况呢?答:边角边(SAS) 边边角(SSA)已知:∠A=600、BC=4cm、AB=3cm小结:方法2:两边和它们的夹角对应相等的两个三角形全等.剪下来,与同伴进行比较,它们能否互相重合?活动2:
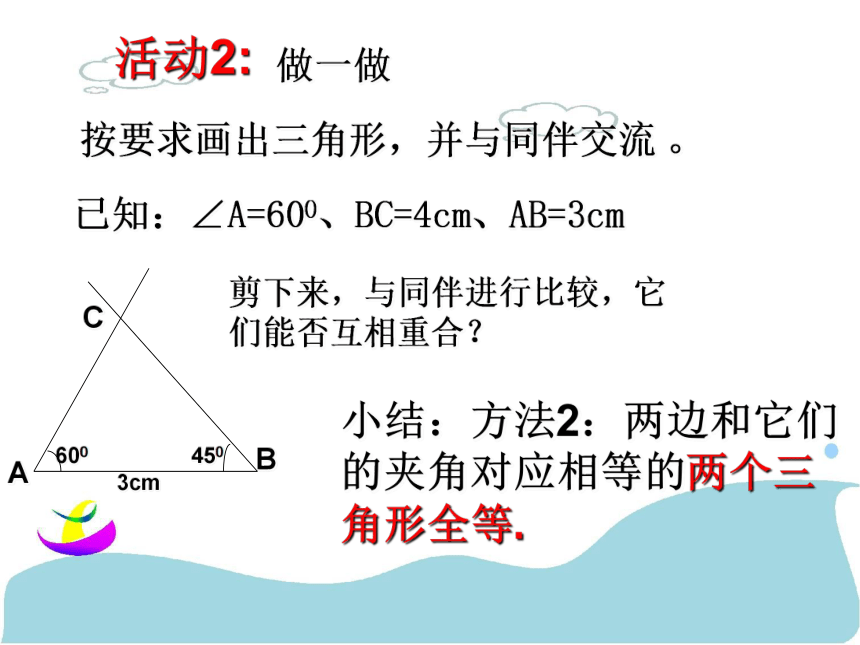
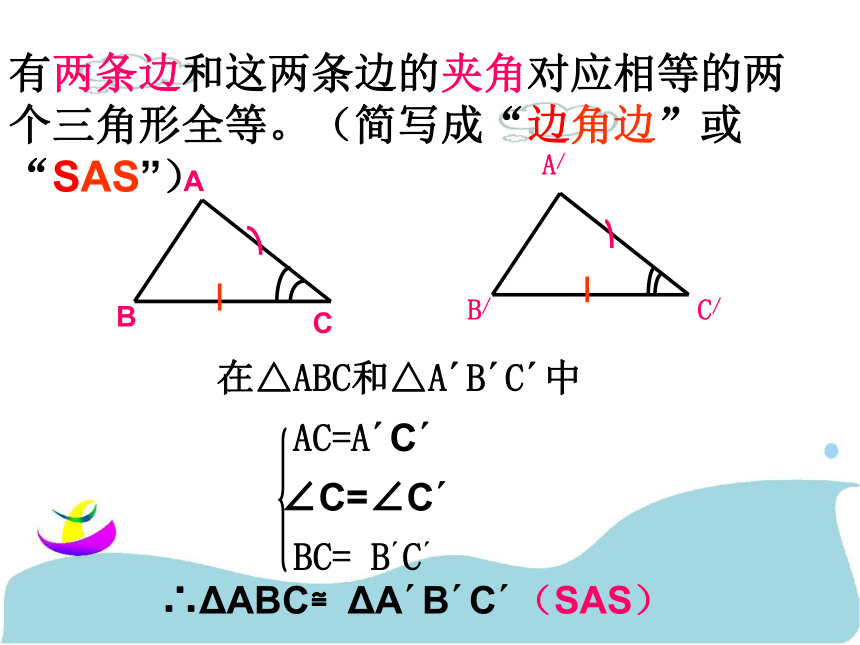
做一做按要求画出三角形,并与同伴交流 。在△ABC和△A′B′C′中
AC=A′C′
∠C=∠C′
BC= B′C′
∴ΔABC≌ΔA′B′C′(SAS)有两条边和这两条边的夹角对应相等的两
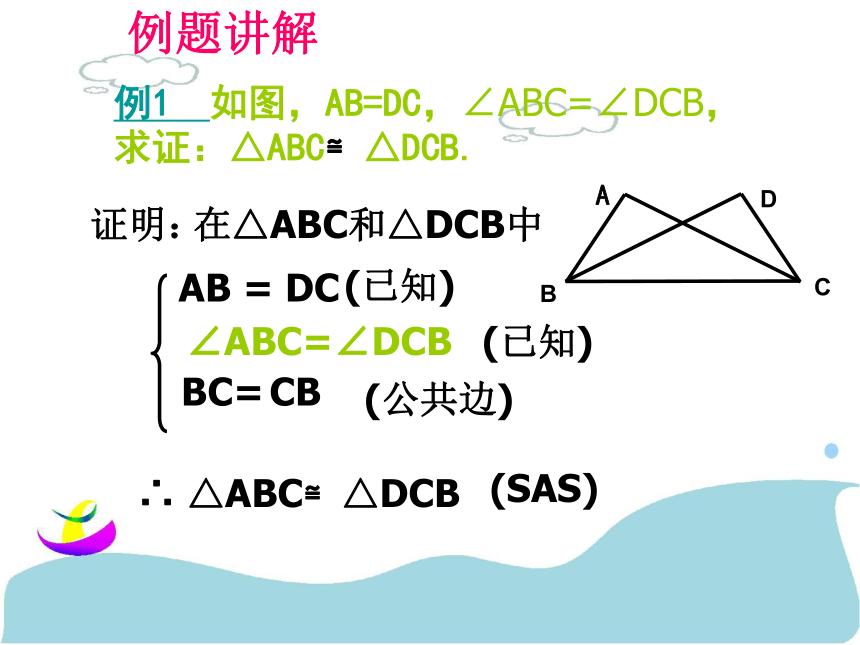
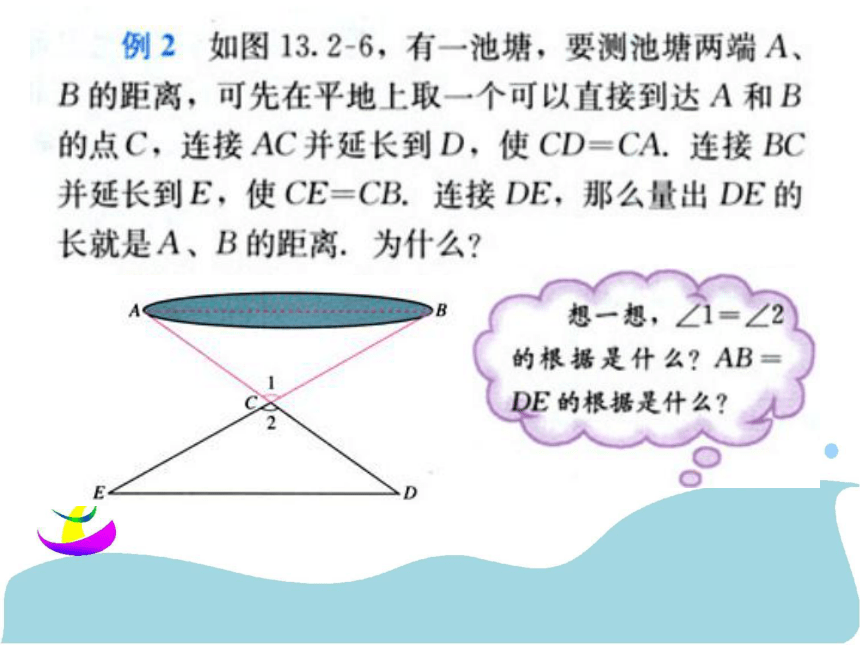
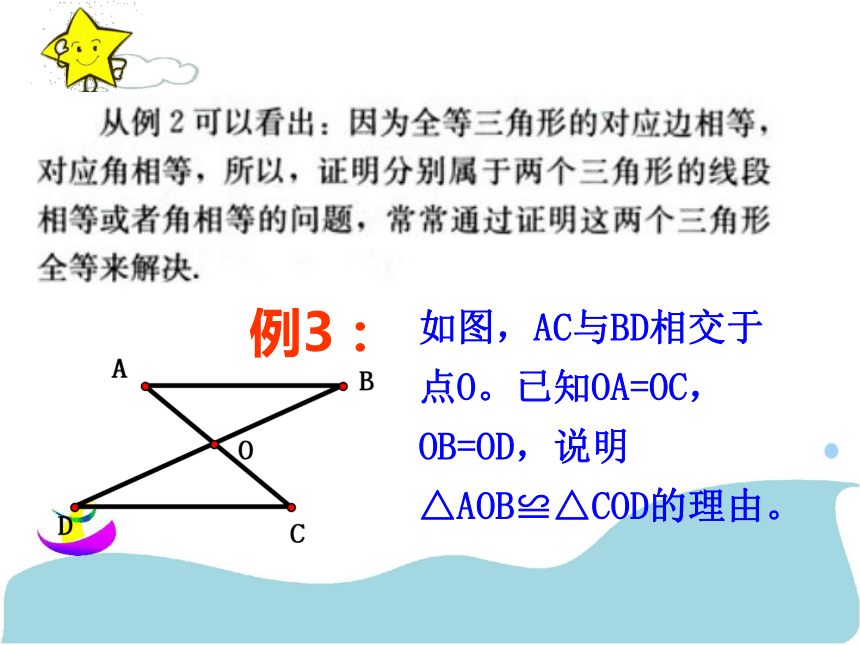
个三角形全等。(简写成“边角边”或“SAS”)例1 如图,AB=DC,∠ABC=∠DCB,求证:△ABC≌△DCB.例题讲解证明: 在△ABC和△DCB中AB = DCBC=CB∴ △ABC≌△DCB(SAS)(公共边)(已知)(已知)∠ABC=∠DCB例3:如图,AC与BD相交于点O。已知OA=OC,OB=OD,说明△AOB≌△COD的理由。例4.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
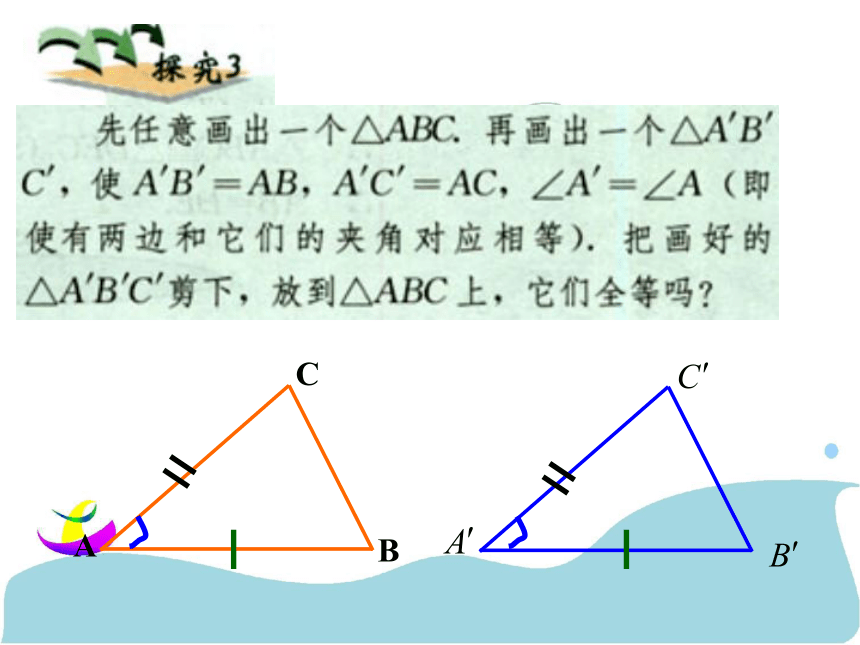
还需增加一个什么条件? 我们知道,两边和它们的
夹角对应相等的两个三角形全
等。由“两边及其中一边的对角
对应相等”的条件能判定两个三
角形全等吗?为什么?探究2ABCD练一练AB=DE,求证:AC=DF, ∠A= ∠D
AC∥DF探究:
如图,AE=AD, AB=AC ,则∠1=∠2吗?为什么?同学们再见!练一练 如图,在△ABC和△ DEF 中,已知
AB= DE ,∠B= ∠E、 ∠C= ∠F ,
△ ABC和 △ DEF 会全等吗?为什么?问题3:做一做:按要求画三角形,并与同伴交流
已知:∠A=600、∠B=450、BC=3cm
BCA7504503cm小结:方法3:两角和其中一角的对边对应相等的两个三角形全等,简写成角角边或AAS剪下来,与同伴进行比较,它们能否互相重合? 两角和其中一角的对边对应相等的两个三角形全等。(简写成“角角边”或“AAS”)在△ABC和△DEF中
∠C=∠F
∠B=∠E
AB=DE
∴ΔABC≌ΔDEF(AAS)方法2:∵∠B=∠E,BC=EF,∠C=∠F
∴ΔABC≌DEF(ASA)方法3:∵ ∠B=∠E ,∠C=∠F,AC=DF
∴Δ ABC≌DEF (AAS)四、想一想 见书本143页2、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
如果已知一个三角形的两条边及一个角,画一个三角形,那么有几种可能的情况呢?答:边角边(SAS) 边边角(SSA)已知:∠A=600、BC=4cm、AB=3cm小结:方法2:两边和它们的夹角对应相等的两个三角形全等.剪下来,与同伴进行比较,它们能否互相重合?活动2:
做一做按要求画出三角形,并与同伴交流 。在△ABC和△A′B′C′中
AC=A′C′
∠C=∠C′
BC= B′C′
∴ΔABC≌ΔA′B′C′(SAS)有两条边和这两条边的夹角对应相等的两
个三角形全等。(简写成“边角边”或“SAS”)例1 如图,AB=DC,∠ABC=∠DCB,求证:△ABC≌△DCB.例题讲解证明: 在△ABC和△DCB中AB = DCBC=CB∴ △ABC≌△DCB(SAS)(公共边)(已知)(已知)∠ABC=∠DCB例3:如图,AC与BD相交于点O。已知OA=OC,OB=OD,说明△AOB≌△COD的理由。例4.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,
还需增加一个什么条件? 我们知道,两边和它们的
夹角对应相等的两个三角形全
等。由“两边及其中一边的对角
对应相等”的条件能判定两个三
角形全等吗?为什么?探究2ABCD练一练AB=DE,求证:AC=DF, ∠A= ∠D
AC∥DF探究:
如图,AE=AD, AB=AC ,则∠1=∠2吗?为什么?同学们再见!练一练 如图,在△ABC和△ DEF 中,已知
AB= DE ,∠B= ∠E、 ∠C= ∠F ,
△ ABC和 △ DEF 会全等吗?为什么?问题3:做一做:按要求画三角形,并与同伴交流
已知:∠A=600、∠B=450、BC=3cm
BCA7504503cm小结:方法3:两角和其中一角的对边对应相等的两个三角形全等,简写成角角边或AAS剪下来,与同伴进行比较,它们能否互相重合? 两角和其中一角的对边对应相等的两个三角形全等。(简写成“角角边”或“AAS”)在△ABC和△DEF中
∠C=∠F
∠B=∠E
AB=DE
∴ΔABC≌ΔDEF(AAS)方法2:∵∠B=∠E,BC=EF,∠C=∠F
∴ΔABC≌DEF(ASA)方法3:∵ ∠B=∠E ,∠C=∠F,AC=DF
∴Δ ABC≌DEF (AAS)四、想一想 见书本143页2、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
