空间向量与立体几何试卷及答案(含解析)
文档属性
| 名称 | 空间向量与立体几何试卷及答案(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 585.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 00:00:00 | ||
图片预览



文档简介
空间向量与立体几何测试(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.满足下列条件,能说明空间不重合的A,B,C三点共线的是( )
A.+= B.-=
C.= D.||=||
2.如图,在大小为45°的二面角A EF C中,四边形ABFE,CDEF都是边长为1的正方形,则B,D两点间的距离是( )
A. B.
C.1 D.
3.在四面体OABC中,G1是△ABC的重心,G是OG1上的一点,且OG=3GG1,若=x+y+,则(x,y,z)为( )
A. B.
C. D.
4.若点P(-4,-2,3)关于Oxy平面及y轴对称的点的坐标分别是(a,b,c),(e,f,d),则c与e的和为( )
A.7 B.-7
C.-1 D.1
5.如图,已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE的中点,FM=MA,则线段OM的长为( )
A.3 B.
C.2 D.
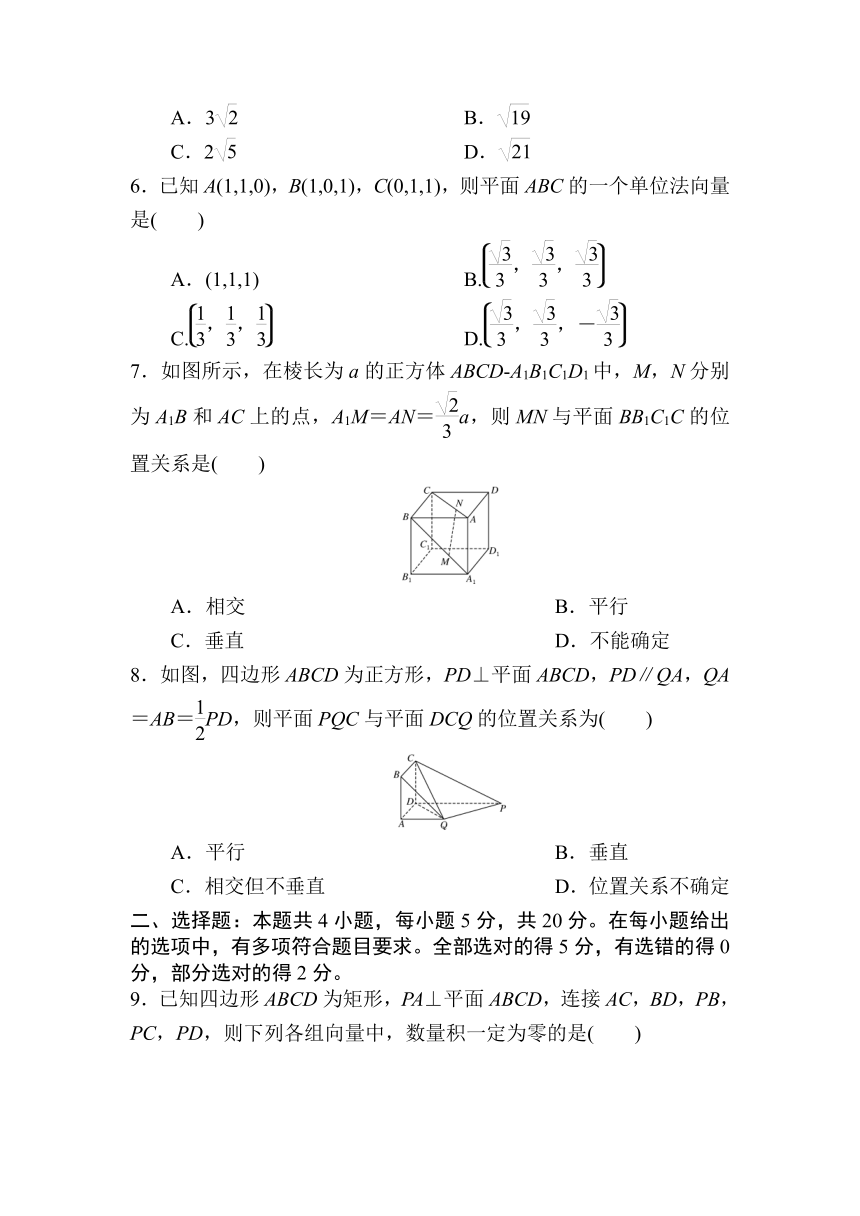
6.已知A(1,1,0),B(1,0,1),C(0,1,1),则平面ABC的一个单位法向量是( )
A.(1,1,1) B.
C. D.
7.如图所示,在棱长为a的正方体ABCD A1B1C1D1中,M,N分别为A1B和AC上的点,A1M=AN=a,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.不能确定
8.如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD,则平面PQC与平面DCQ的位置关系为( )
A.平行 B.垂直
C.相交但不垂直 D.位置关系不确定
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积一定为零的是( )
A.与 B.与
C.与 D.与
10.若向量a=(1,2,0),b=(-2,0,1),则 ( )
A.cos〈a,b〉=- B.a⊥b
C.a∥b D.|a|=|b|
11.已知平面α内有一点A(2,-1,2),平面α的一个法向量为n=,则下列四个点中在平面α内的是( )
A.P1 B.P2
C.P3 D.P4
12.如图所示,正方体ABCD A1B1C1D1中,AB=1,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则以下四个结论正确的是( )
A.VP AA1D=
B.点P必在线段B1C上
C.AP⊥BC1
D.AP∥平面A1C1D
三、填空题:本题共4小题,每小题5分,共20分。把答案填在题中横线上。
13.已知空间向量c,d不共线,设向量a=kc+d,b=c-k2d,且a与b共线,则实数k的值为________。
14.如图,在正三棱柱ABC A1B1C1中,M为△A1B1C1的重心,若=a,=b,=c,则=________。
15.如图所示,正四面体ABCD的棱长为1,G是△BCD的中心,建立如图所示的空间直角坐标系,则的坐标为________,的坐标为________。
16.已知三棱锥O ABC, OA=OB=1,OC=2,OA,OB,OC两两垂直,存在一点D,使BD∥AC,DC∥AB,则D的坐标为________。
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
如图,BC=2,原点O是BC的中点,点A的坐标为,点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
(1)求向量的坐标.
(2)求与的夹角的余弦值.
18.(本小题满分12分)
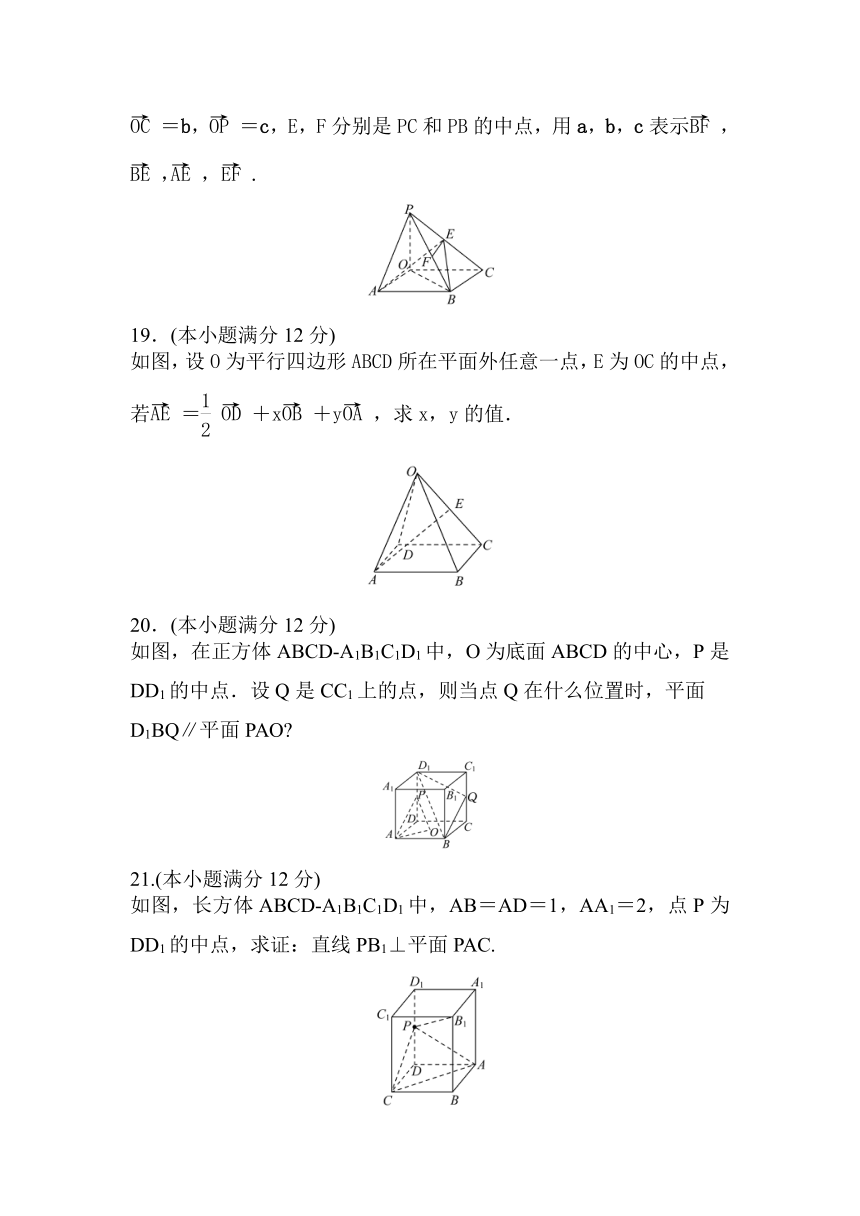
如图,四棱锥P OABC的底面为一矩形,PO⊥平面OABC,设=a,=b,=c,E,F分别是PC和PB的中点,用a,b,c表示,,,.
19.(本小题满分12分)
如图,设O为平行四边形ABCD所在平面外任意一点,E为OC的中点,若=+x+y,求x,y的值.
20.(本小题满分12分)
如图,在正方体ABCD A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点.设Q是CC1上的点,则当点Q在什么位置时,平面D1BQ∥平面PAO
21.(本小题满分12分)
如图,长方体ABCD A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,求证:直线PB1⊥平面PAC.
22.(本小题满分12分)
如图,在四棱锥P ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,M是PD上一点,且BM⊥PD.
(1)求异面直线PB与CM所成角的余弦值;
(2)求点M到平面PAC的距离.
参考答案
1解析 对于空间中的任意向量,都有+=,选项A错误;若-=,则+=,而+=,据此可知=,即B,C两点重合,选项B错误;=,则A,B,C三点共线,选项C正确;||=||,则线段AB的长度与线段BC的长度相等,不一定有A,B,C三点共线,选项D错误。
答案 C
2解析 因为=++,所以||2=||2+||2+||2+2·+2·+2·=1+1+1-=3-,故||=。
答案 D
3解析 如图所示,连接AG1并延长,交BC于点E,则E为BC中点,=(+)=(-2+),= =(-2+)。因为=3=3(-),所以OG=OG1。则==(+)=(+-+)=++,所以x=,y=,z=。
答案 A
4解析 由题意,知点P关于Oxy平面对称的点的坐标为(-4,-2,-3),点P关于y轴对称的点的坐标为(4,-2,-3),故c=-3,e=4,故c+e=-3+4=1。
答案 D
5解析 由题意可建立以D为原点,DA,DC,DE所在直线分别为x轴,y轴,z轴的空间直角坐标系(图略),则E(0,0,6),B(6,6,0),M(6,0,4),O(3,3,3),所以|OM|==,即线段OM的长为。故选B。
答案 B
6解析 设平面ABC的法向量为n=(x,y,z),又=(0,-1,1),=(-1,1,0),则所以x=y=z,又因为单位向量的模为1,故只有B正确。
答案 B
7解析 如图,分别以C1B1,C1D1,C1C所在直线为x,y,z轴,建立空间直角坐标系。因为A1M=AN=a,所以M,N,所以=。又C1(0,0,0),D1(0,a,0),所以=(0,a,0)。所以·=0。所以⊥。因为是平面BB1C1C的一个法向量,且MN 平面BB1C1C,所以MN∥平面BB1C1C。
答案 B
8解析 由已知可得PD⊥DC,PD⊥DA,DC⊥DA,如图,以D为原点,建立空间直角坐标系,设QA=1,则D(0,0,0),C(0,0,1),Q(1,1,0),P(0,2,0)。故=(1,1,0),=(0,0,1),=(1,-1,0)。故·=0,·=0,即⊥,⊥,又DQ∩DC=D,故PQ⊥平面DCQ,又PQ 平面PQC,所以平面PQC⊥平面DCQ。
答案 B
9解析 因为PA⊥平面ABCD,CD 平面ABCD,所以PA⊥CD,故·=0;因为由PA⊥平面ABCD,可得PA⊥AD,又AD⊥AB,PA∩AB=A,所以AD⊥平面PAB,又PB 平面PAB,所以AD⊥PB,故·=0;同理·=0。故选BCD。
答案 BCD
10解析 因为向量a=(1,2,0),b=(-2,0,1),所以|a|=,|b|=,a·b=1×(-2)+2×0+0×1=-2,cos〈a,b〉===-。由上知B,C不正确,A,D正确。
答案 AD
11解析 对于选项A中的点P1,=,·n=0,A成立,对于选项B中的点P2 ,=,所以·n=0。同理C,D不正确。故选AB。
答案 AB
12解析 对于A,因为P在平面BCC1B1上,平面BCC1B1∥平面AA1D,所以P到平面AA1D即为C到平面AA1D的距离,即为正方体棱长,所以VP AA1D=S△AA1D·CD=××1×1×1=,A错误;对于B,以D为原点可建立如图所示的空间直角坐标系,
则A(1,0,0),P(x,1,z),B(1,1,0),D1(0,0,1),B1(1,1,1),C(0,1,0),所以=(x-1,1,z),=(-1,-1,1),=(-1,0,-1),因为AP⊥BD1,所以·=1-x-1+z=0,所以x=z,即P(x,1,x),所以=(x,0,x),所以=-x,即B1,P,C三点共线,所以P必在线段B1C上,B正确。对于C,因为=(x-1,1,x),=(-1,0,1),所以·=1-x+x=1,所以AP与BC1不垂直,C错误。对于D,因为A1(1,0,1),C1(0,1,1),D(0,0,0),所以=(1,0,1),=(0,1,1),设平面A1C1D的一个法向量为n=(x,y,z),所以令x=1,则z=-1,y=1,所以n=(1,1,-1),所以·n=x-1+1-x=0,即⊥n,所以AP∥平面A1C1D,D正确。故选BD。
答案 BD
13解析 因为c,d不共线,所以c≠0,且d≠0。由a与b共线知,存在λ∈R使a=λb成立,即kc+d=λ(c-k2d),整理得(k-λ)c+(1+λk2)d=0,所以解得k=λ=-1。
答案 -1
14解析 =+=+=+(-)=+=-+=a-b+c。
答案 a-b+c
15解析 由题意可知,BG=BE=×=,所以AG==,所以=,=-=。
答案
16解析 建立如图所示的空间直角坐标系,则A(1,0,0),B(0,1,0),C(0,0,2),设所求点D(x,y,z)。由BD∥AC,DC∥AB ∥,∥,因此, 即点D的坐标为(-1,1,2)。
答案 (-1,1,2)
17解析(1)过D作DE⊥BC于E,则DE=CD·sin 30°=,OE=OB-BD cos 60°=1-=,所以D点坐标为,又因为C(0,1,0),所以=.
(2)依题设,A点坐标为,所以=,=(0,2,0),则与的夹角的余弦值为cos 〈,〉
==-.
18解析 ==-=-(+)=-a-b+c;=-=(+)-(+)
=--+=-a-b+c;=-=(+)-=-a+b+c;===a.
19解析 因为=++=-+--=-+=-+(+)=-+(+)=-++(-)=-++,所以x=,y=-.
20解析 建立如图所示的空间直角坐标系,设正方体的棱长为2,
则O(1,1,0),A(2,0,0),P(0,0,1),B(2,2,0),D1(0,0,2),所以=(1,-1,0),=(-1,-1,1),=(-2,-2,2).设平面PAO的法向量为n1=(x,y,z),则 令x=1,则y=1,z=2,所以平面PAO的一个法向量为n1=(1,1,2).若平面D1BQ∥平面PAO,则n1也是平面D1BQ的一个法向量.设Q(0,2,c),则=(-2,0,c),n1·=0,即-2+2c=0,所以c=1,这时n1·=-2-2+4=0.所以当Q为CC1的中点时,平面D1BQ∥平面PAO.
21证明依题设,以D为坐标原点,如图所示,建立空间直角坐标系Dxyz,则C(1,0,0),P(0,0,1),A(0,1,0),B1(1,1,2),
于是=(-1,1,0),=(-1,0,1),=(1,1,1),
所以·=(-1,1,0)·(1,1,1)=0,·=(-1,0,1)·(1,1,1)=0,故⊥,⊥,即PB1⊥CP,PB1⊥CA,又CP∩CA=C,且CP 平面PAC,CA 平面PAC.故直线PB1⊥平面PAC.
22解析 (1)分别以AB,AD,AP所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,A,B,C,D,P,
则=,=,=,设=λ(0≤λ≤1),则=,所以=-=,由BM⊥PD知·=0+16λ-4=0,所以λ=,M为PD的中点,所以M,=,cos 〈,〉===-.所以异面直线PB与CM所成角的余弦值为.
(2)=,=,设平面PAC的法向量为n=,由得所以z=0,取x=2,得y=-1,所以n=是平面PAC的一个法向量.
所以点M到平面PAC的距离为==.
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.满足下列条件,能说明空间不重合的A,B,C三点共线的是( )
A.+= B.-=
C.= D.||=||
2.如图,在大小为45°的二面角A EF C中,四边形ABFE,CDEF都是边长为1的正方形,则B,D两点间的距离是( )
A. B.
C.1 D.
3.在四面体OABC中,G1是△ABC的重心,G是OG1上的一点,且OG=3GG1,若=x+y+,则(x,y,z)为( )
A. B.
C. D.
4.若点P(-4,-2,3)关于Oxy平面及y轴对称的点的坐标分别是(a,b,c),(e,f,d),则c与e的和为( )
A.7 B.-7
C.-1 D.1
5.如图,已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE的中点,FM=MA,则线段OM的长为( )
A.3 B.
C.2 D.
6.已知A(1,1,0),B(1,0,1),C(0,1,1),则平面ABC的一个单位法向量是( )
A.(1,1,1) B.
C. D.
7.如图所示,在棱长为a的正方体ABCD A1B1C1D1中,M,N分别为A1B和AC上的点,A1M=AN=a,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行
C.垂直 D.不能确定
8.如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD,则平面PQC与平面DCQ的位置关系为( )
A.平行 B.垂直
C.相交但不垂直 D.位置关系不确定
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积一定为零的是( )
A.与 B.与
C.与 D.与
10.若向量a=(1,2,0),b=(-2,0,1),则 ( )
A.cos〈a,b〉=- B.a⊥b
C.a∥b D.|a|=|b|
11.已知平面α内有一点A(2,-1,2),平面α的一个法向量为n=,则下列四个点中在平面α内的是( )
A.P1 B.P2
C.P3 D.P4
12.如图所示,正方体ABCD A1B1C1D1中,AB=1,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则以下四个结论正确的是( )
A.VP AA1D=
B.点P必在线段B1C上
C.AP⊥BC1
D.AP∥平面A1C1D
三、填空题:本题共4小题,每小题5分,共20分。把答案填在题中横线上。
13.已知空间向量c,d不共线,设向量a=kc+d,b=c-k2d,且a与b共线,则实数k的值为________。
14.如图,在正三棱柱ABC A1B1C1中,M为△A1B1C1的重心,若=a,=b,=c,则=________。
15.如图所示,正四面体ABCD的棱长为1,G是△BCD的中心,建立如图所示的空间直角坐标系,则的坐标为________,的坐标为________。
16.已知三棱锥O ABC, OA=OB=1,OC=2,OA,OB,OC两两垂直,存在一点D,使BD∥AC,DC∥AB,则D的坐标为________。
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
如图,BC=2,原点O是BC的中点,点A的坐标为,点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
(1)求向量的坐标.
(2)求与的夹角的余弦值.
18.(本小题满分12分)
如图,四棱锥P OABC的底面为一矩形,PO⊥平面OABC,设=a,=b,=c,E,F分别是PC和PB的中点,用a,b,c表示,,,.
19.(本小题满分12分)
如图,设O为平行四边形ABCD所在平面外任意一点,E为OC的中点,若=+x+y,求x,y的值.
20.(本小题满分12分)
如图,在正方体ABCD A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点.设Q是CC1上的点,则当点Q在什么位置时,平面D1BQ∥平面PAO
21.(本小题满分12分)
如图,长方体ABCD A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,求证:直线PB1⊥平面PAC.
22.(本小题满分12分)
如图,在四棱锥P ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,M是PD上一点,且BM⊥PD.
(1)求异面直线PB与CM所成角的余弦值;
(2)求点M到平面PAC的距离.
参考答案
1解析 对于空间中的任意向量,都有+=,选项A错误;若-=,则+=,而+=,据此可知=,即B,C两点重合,选项B错误;=,则A,B,C三点共线,选项C正确;||=||,则线段AB的长度与线段BC的长度相等,不一定有A,B,C三点共线,选项D错误。
答案 C
2解析 因为=++,所以||2=||2+||2+||2+2·+2·+2·=1+1+1-=3-,故||=。
答案 D
3解析 如图所示,连接AG1并延长,交BC于点E,则E为BC中点,=(+)=(-2+),= =(-2+)。因为=3=3(-),所以OG=OG1。则==(+)=(+-+)=++,所以x=,y=,z=。
答案 A
4解析 由题意,知点P关于Oxy平面对称的点的坐标为(-4,-2,-3),点P关于y轴对称的点的坐标为(4,-2,-3),故c=-3,e=4,故c+e=-3+4=1。
答案 D
5解析 由题意可建立以D为原点,DA,DC,DE所在直线分别为x轴,y轴,z轴的空间直角坐标系(图略),则E(0,0,6),B(6,6,0),M(6,0,4),O(3,3,3),所以|OM|==,即线段OM的长为。故选B。
答案 B
6解析 设平面ABC的法向量为n=(x,y,z),又=(0,-1,1),=(-1,1,0),则所以x=y=z,又因为单位向量的模为1,故只有B正确。
答案 B
7解析 如图,分别以C1B1,C1D1,C1C所在直线为x,y,z轴,建立空间直角坐标系。因为A1M=AN=a,所以M,N,所以=。又C1(0,0,0),D1(0,a,0),所以=(0,a,0)。所以·=0。所以⊥。因为是平面BB1C1C的一个法向量,且MN 平面BB1C1C,所以MN∥平面BB1C1C。
答案 B
8解析 由已知可得PD⊥DC,PD⊥DA,DC⊥DA,如图,以D为原点,建立空间直角坐标系,设QA=1,则D(0,0,0),C(0,0,1),Q(1,1,0),P(0,2,0)。故=(1,1,0),=(0,0,1),=(1,-1,0)。故·=0,·=0,即⊥,⊥,又DQ∩DC=D,故PQ⊥平面DCQ,又PQ 平面PQC,所以平面PQC⊥平面DCQ。
答案 B
9解析 因为PA⊥平面ABCD,CD 平面ABCD,所以PA⊥CD,故·=0;因为由PA⊥平面ABCD,可得PA⊥AD,又AD⊥AB,PA∩AB=A,所以AD⊥平面PAB,又PB 平面PAB,所以AD⊥PB,故·=0;同理·=0。故选BCD。
答案 BCD
10解析 因为向量a=(1,2,0),b=(-2,0,1),所以|a|=,|b|=,a·b=1×(-2)+2×0+0×1=-2,cos〈a,b〉===-。由上知B,C不正确,A,D正确。
答案 AD
11解析 对于选项A中的点P1,=,·n=0,A成立,对于选项B中的点P2 ,=,所以·n=0。同理C,D不正确。故选AB。
答案 AB
12解析 对于A,因为P在平面BCC1B1上,平面BCC1B1∥平面AA1D,所以P到平面AA1D即为C到平面AA1D的距离,即为正方体棱长,所以VP AA1D=S△AA1D·CD=××1×1×1=,A错误;对于B,以D为原点可建立如图所示的空间直角坐标系,
则A(1,0,0),P(x,1,z),B(1,1,0),D1(0,0,1),B1(1,1,1),C(0,1,0),所以=(x-1,1,z),=(-1,-1,1),=(-1,0,-1),因为AP⊥BD1,所以·=1-x-1+z=0,所以x=z,即P(x,1,x),所以=(x,0,x),所以=-x,即B1,P,C三点共线,所以P必在线段B1C上,B正确。对于C,因为=(x-1,1,x),=(-1,0,1),所以·=1-x+x=1,所以AP与BC1不垂直,C错误。对于D,因为A1(1,0,1),C1(0,1,1),D(0,0,0),所以=(1,0,1),=(0,1,1),设平面A1C1D的一个法向量为n=(x,y,z),所以令x=1,则z=-1,y=1,所以n=(1,1,-1),所以·n=x-1+1-x=0,即⊥n,所以AP∥平面A1C1D,D正确。故选BD。
答案 BD
13解析 因为c,d不共线,所以c≠0,且d≠0。由a与b共线知,存在λ∈R使a=λb成立,即kc+d=λ(c-k2d),整理得(k-λ)c+(1+λk2)d=0,所以解得k=λ=-1。
答案 -1
14解析 =+=+=+(-)=+=-+=a-b+c。
答案 a-b+c
15解析 由题意可知,BG=BE=×=,所以AG==,所以=,=-=。
答案
16解析 建立如图所示的空间直角坐标系,则A(1,0,0),B(0,1,0),C(0,0,2),设所求点D(x,y,z)。由BD∥AC,DC∥AB ∥,∥,因此, 即点D的坐标为(-1,1,2)。
答案 (-1,1,2)
17解析(1)过D作DE⊥BC于E,则DE=CD·sin 30°=,OE=OB-BD cos 60°=1-=,所以D点坐标为,又因为C(0,1,0),所以=.
(2)依题设,A点坐标为,所以=,=(0,2,0),则与的夹角的余弦值为cos 〈,〉
==-.
18解析 ==-=-(+)=-a-b+c;=-=(+)-(+)
=--+=-a-b+c;=-=(+)-=-a+b+c;===a.
19解析 因为=++=-+--=-+=-+(+)=-+(+)=-++(-)=-++,所以x=,y=-.
20解析 建立如图所示的空间直角坐标系,设正方体的棱长为2,
则O(1,1,0),A(2,0,0),P(0,0,1),B(2,2,0),D1(0,0,2),所以=(1,-1,0),=(-1,-1,1),=(-2,-2,2).设平面PAO的法向量为n1=(x,y,z),则 令x=1,则y=1,z=2,所以平面PAO的一个法向量为n1=(1,1,2).若平面D1BQ∥平面PAO,则n1也是平面D1BQ的一个法向量.设Q(0,2,c),则=(-2,0,c),n1·=0,即-2+2c=0,所以c=1,这时n1·=-2-2+4=0.所以当Q为CC1的中点时,平面D1BQ∥平面PAO.
21证明依题设,以D为坐标原点,如图所示,建立空间直角坐标系Dxyz,则C(1,0,0),P(0,0,1),A(0,1,0),B1(1,1,2),
于是=(-1,1,0),=(-1,0,1),=(1,1,1),
所以·=(-1,1,0)·(1,1,1)=0,·=(-1,0,1)·(1,1,1)=0,故⊥,⊥,即PB1⊥CP,PB1⊥CA,又CP∩CA=C,且CP 平面PAC,CA 平面PAC.故直线PB1⊥平面PAC.
22解析 (1)分别以AB,AD,AP所在直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,A,B,C,D,P,
则=,=,=,设=λ(0≤λ≤1),则=,所以=-=,由BM⊥PD知·=0+16λ-4=0,所以λ=,M为PD的中点,所以M,=,cos 〈,〉===-.所以异面直线PB与CM所成角的余弦值为.
(2)=,=,设平面PAC的法向量为n=,由得所以z=0,取x=2,得y=-1,所以n=是平面PAC的一个法向量.
所以点M到平面PAC的距离为==.
