圆锥曲线的方程试卷及答案(含解析)
文档属性
| 名称 | 圆锥曲线的方程试卷及答案(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-19 11:06:19 | ||
图片预览




文档简介
圆锥曲线的方程测试(时间:120分钟 满分:150分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.中心在原点,焦点在坐标轴上,且过两点(4,0),(0,2)的椭圆方程为( )
A.+=1 B.+=1
C.+=1 D.+=1
2.已知双曲线+=1的焦点在x轴上,若该双曲线的焦距为4,则a等于( )
A.1 B.
C.4 D.10
3.若双曲线与椭圆+=1有相同的焦点,它的一条渐近线方程为y=-x,则双曲线的方程为( )
A.y2-x2=96 B.y2-x2=160
C.y2-x2=80 D.y2-x2=24
4.已知动点M的坐标满足方程5=|3x+4y-12|,则动点M的轨迹是( )
A.椭圆 B.双曲线
C.抛物线 D.圆
5.已知抛物线y2=2px(p>0)的准线与曲线x2+y2-4x-5=0相切,则p的值为( )
A.2 B.1
C. D.
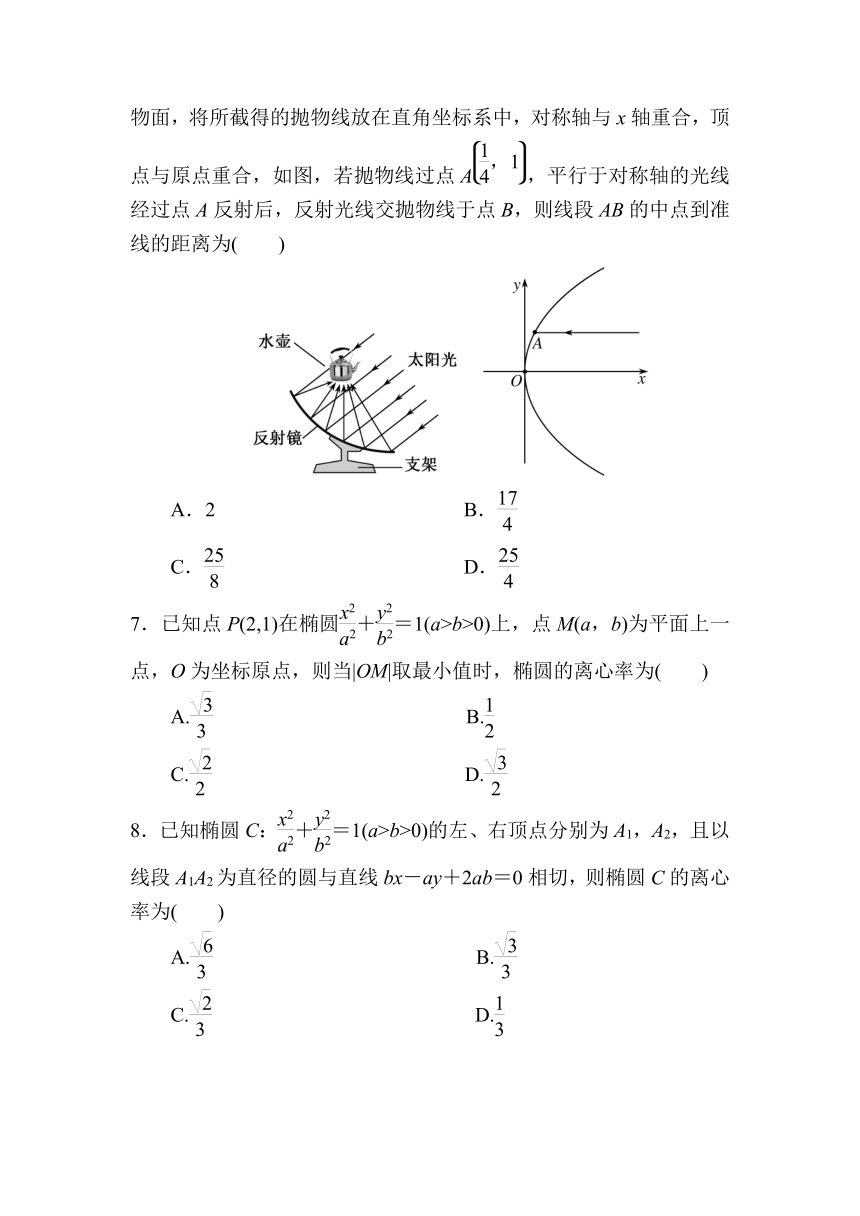
6.由抛物线绕它的对称轴旋转所得到的曲面叫抛物面,用于加热水和食物的太阳灶应用了抛物线的光学性质:一束平行于抛物线轴的光线,经过抛物面的反射集中于它的焦点。用一过抛物线轴的平面截抛物面,将所截得的抛物线放在直角坐标系中,对称轴与x轴重合,顶点与原点重合,如图,若抛物线过点A,平行于对称轴的光线经过点A反射后,反射光线交抛物线于点B,则线段AB的中点到准线的距离为( )
A.2 B.
C. D.
7.已知点P(2,1)在椭圆+=1(a>b>0)上,点M(a,b)为平面上一点,O为坐标原点,则当|OM|取最小值时,椭圆的离心率为( )
A. B.
C. D.
8.已知椭圆C:+=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切,则椭圆C的离心率为( )
A. B.
C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.对于曲线C:+=1,下面四个说法中正确的是( )
A.曲线C不可能是椭圆
B.“1C.“曲线C是焦点在y轴上的椭圆”是“3D.“曲线C是焦点在x轴上的椭圆”是“110.已知F1,F2分别是双曲线C:y2-x2=1的上、下焦点,点P是其一条渐近线上的点,且以线段F1F2为直径的圆经过点P,则( )
A.双曲线C的渐近线方程为y=±x
B.以F1F2为直径的圆的方程为x2+y2=1
C.点P的横坐标为±1
D.△PF1F2的面积为
11.已知双曲线C过点且渐近线为y=±x,则下列结论正确的是( )
A.C的方程为-y2=1
B.C的离心率为
C.曲线y=ex-2-1经过C的一个焦点
D.直线x-y-1=0与C有两个公共点
12.已知抛物线y2=2px(p>0)的焦点为F,过F的直线l交抛物线于A(x1,y1),B(x2,y2)两点(点A在第一象限),则下列结论中正确的是( )
A.x1x2=
B.+=
C.若直线l的倾斜角为,则=3
D.若直线l的倾斜角为,则|AB|=4p
三、填空题:本题共4小题,每小题5分,共20分。把答案填在题中横线上。
13.已知椭圆的短半轴长为1,离心率014.抛物线方程为7x+4y2=0,则焦点坐标为________。
15.已知动点M与两定点A(-1,0),B(1,0)构成△MAB,且直线MA,MB的斜率之积为4。设动点M的轨迹为C,则轨迹C的方程为______________。
16.已知点M和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°,则k=________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知椭圆中心在坐标原点,焦点在x轴上,椭圆与x轴的一个交点到两焦点的距离分别为3和1,求椭圆的标准方程.
18.(本小题满分12分)
已知抛物线y2=2x的焦点为F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求此时P点的坐标.
19.(本小题满分12分)
若方程+=-1表示焦点在y轴上的双曲线,求它的半焦距c的取值范围.
20.(本小题满分12分)
已知椭圆C的中心在原点,一个焦点为F(-2,0),且长轴长与短轴长的比是2∶.
(1)求椭圆C的方程.
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
21.(本小题满分12分)
已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3.
(1)求抛物线E的方程;
(2)已知点G(-1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
22.(本小题满分12分)
已知双曲线C:-=1(a>0,b>0)的离心率为,虚轴长为4.
(1)求双曲线的标准方程.
(2)过点(0,1),倾斜角为45°的直线l与双曲线C相交于A,B两点,O为坐标原点,求△OAB的面积.
参考答案
1解析 解法一:验证排除,将点(4,0)代入验证可排除A,B,C。故选D。
解法二:设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n),则解得故选D。
答案 D
2解析 根据题意可知,双曲线的标准方程为-=1。由双曲线的焦距为4,得c=2,则有c2=a-3+a-1=4,解得a=4。
答案 C
3解析 设双曲线方程为x2-y2=λ(λ≠0),因为双曲线与椭圆有相同的焦点,且焦点为(0,±4),所以λ<0,且-2λ=(4)2,得λ=-24。故选D。
答案 D
4解析 方程5=|3x+4y-12|可化为=,它表示点M到坐标原点O的距离等于它到直线3x+4y-12=0的距离,由抛物线的定义,可知动点M的轨迹是抛物线。故选C。
答案 C
5解析 曲线的方程可化为(x-2)2+y2=9,其表示圆心为(2,0),半径为3的圆,又抛物线的准线方程为x=-,所以由抛物线的准线与圆相切得2+=3。解得p=2。
答案 A
6解析 设抛物线方程为y2=2px,将点A代入可得1=2p×,解得p=2,所以抛物线方程为y2=4x,焦点为F(1,0),准线为x=-1。由题意可得,直线AB的方程为y-0=(x-1),即y=-(x-1),由可得y2+3y-4=0,解得或所以A,B(4,-4),可得AB的中点为,所以线段AB的中点到准线的距离为+1=。故选C。
答案 C
7解析 点P(2,1)在椭圆+=1(a>b>0)上,可得+=1,M(a,b)为平面上一点,O为坐标原点,则|OM|==≥=3,当且仅当a2=2b2时,等号成立,此时由解得a2=6,b2=3。所以e===。故选C。
答案 C
8解析 以线段A1A2为直径的圆的方程为x2+y2=a2,因为圆与直线bx-ay+2ab=0相切,所以=a,即2b=,所以a2=3b2。因为a2=b2+c2,所以c2=2b2,所以=,所以e==。故选A。
答案 A
9解析 A项,当1答案 CD
10解析 等轴双曲线C:y2-x2=1的渐近线方程为y=±x,故A正确。由双曲线的方程可知|F1F2|=2,所以以F1F2为直径的圆的方程为x2+y2=2,故B错误。点P(x0,y0)在圆x2+y2=2上,不妨设点P(x0,y0)在直线y=x上,所以解得|x0|=1,则点P的横坐标为±1,故C正确。由上述分析可得△PF1F2的面积为×2×1=,故D正确。故选ACD。
答案 ACD
11解析 对于选项A:由已知y=±x,可得y2=x2,从而设所求双曲线方程为x2-y2=λ,又由双曲线C过点,从而×32-()2=λ,即λ=1,从而选项A正确;对于选项B:由双曲线方程可知a=,b=1,c=2,从而离心率为e===,所以B选项错误;对于选项C:双曲线的右焦点坐标为,满足y=ex-2-1,从而选项C正确;对于选项D:联立,
整理,得y2-2y+2=0,由Δ=(2)2-4×2=0,知直线与双曲线C只有一个交点,选项D错误.
答案 AC
12解析 抛物线y2=2px(p>0)的焦点为F,准线为x=-,当斜率不存在时,则过焦点的直线的方程为x=,则,B,此时x1x2=,+=+=,故B错误;当斜率存在时,设过焦点的直线方程为y=,联立直线与抛物线方程得消去y得k2x2-(k2p+2p)x+=0,由根与系数的关系可得x1x2=,x1+x2=,故A正确;若直线l的倾斜角为,则k=,所以x1+x2==7p,所以|AB|=x1+x2+p=8p,故D错误;过A,B分别作准线的垂线,垂足分别为M,N,作BE⊥AM,垂足为E,设|AF|=m,=n,则由抛物线的定义得=|AF|=m,|BN|=|BF|=n,|AB|=m+n,|AE|=m-n,因为∠EAB=60°,于是=,解得m=3n,则==3,故C正确。综上,正确的有AC。
答案 AC
13解析 因为b=1,所以c2=a2-1。又==1-≤。所以≥,即a2≤4。又a2-1>0,所以a2>1,故1答案 (2,4]
14解析 抛物线方程化为y2=-x,所以抛物线开口向左,2p=,=,故焦点坐标为。
答案
15解析 设点M的坐标为(x,y),当x=-1时,直线MA的斜率不存在;当x=1时,直线MB的斜率不存在。于是x≠1且x≠-1。此时,直线MA的斜率为,直线MB的斜率为。由题意有·=4,化简得x2-=1,因为x≠1且x≠-1,即y≠0,所以轨迹C的方程为x2-=1(y≠0)。
答案 x2-=1(y≠0)
16解析 由抛物线的方程y2=4x可知其焦点F的坐标为(1,0),所以直线AB的方程为y=k(x-1),由得k2x2-2(k2+2)x+k2=0,设A(x1,y1),B(x2,y2),所以x1+x2=,x1x2=1,因为∠AMB=90°,所以·=(x1+1,y1-1)·(x2+1,y2-1)=(x1+1)(x2+1)+(y1-1)(y2-1)=(x1+1)(x2+1)+[k(x1-1)-1]·[k(x2-1)-1]=(1-k-k2)(x1+x2)+(1+k2)x1x2+k2+2k+2
=(1-k-k2)+(1+k2)+k2+2k+2=0,
整理可解得k=2.
答案:2
17解析 由题意可得所以
故b2=a2-c2=3,所以椭圆方程为+=1.
18解析 将x=3代入抛物线方程y2=2x,得y=±.因为>2,所以A在抛物线内部.设抛物线上动点P到准线l:x=-的距离为d,由抛物线的定义,知|PA|+|PF|=|PA|+d.当PA⊥l时,|PA|+d最小,最小值为,即|PA|+|PF|的最小值为,此时P点的纵坐标为2,代入y2=2x,得x=2,所以P点的坐标为(2,2).
19解析 因为方程+=-1两边除以-1,方程可化简为-=1,又因为方程表示为焦点在y轴上的双曲线,
所以k-2>0,-3>0即k>3,从而方程可表示为-=1,由于c2=a2+b2=2k-5>1,所以半焦距c的取值范围为c>1,即c∈.
20解析 (1)由题意知解得所以椭圆C的方程为+=1.
(2)设P(x0,y0),且 eq \f(x,16) + eq \f(y,12) =1,所以2=(x0-m)2+y=x-2mx0+m2+12 eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(x,16))) =x-2mx0+m2+12=(x0-4m)2-3m2+12.所以2为关于x0的二次函数,开口向上,对称轴为4m.由题意知,当x0=4时,2最小,所以4m≥4,所以m≥1.又点M(m,0)在椭圆长轴上,所以1≤m≤4.
21解析 (1)由抛物线的定义,得|AF|=2+.因为|AF|=3,即2+=3,解得p=2,所以抛物线E的方程为y2=4x.
(2)因为点A(2,m)在抛物线E:y2=4x上,所以m=±2,由抛物线的对称性,不妨设 A(2,2).由A(2,2),F(1,0)可得,直线AF的方程为y=2(x-1).由,得2x2-5x+2=0,解得x=2或x=,从而B.又G(-1,0),所以kGA==,kGB==-,
所以kGA+kGB=0,从而∠AGF=∠BGF,这表明点F到直线GA,GB的距离相等,故以F为圆心且与直线GA相切的圆必与直线GB相切.
22解析 (1)依题意可得解得a=1,b=2,c=,
所以双曲线的标准方程为x2-=1.
(2)直线l的方程为y=x+1,联立消去y得3x2-2x-5=0,设A(x1,y1),B(x2,y2)由根与系数的关系可得x1+x2=,x1x2=-,则|AB|=|x1-x2|==×=,原点到直线l的距离为d=,所以S△OAB=·|AB|·d=××=.所以△OAB的面积为.
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.中心在原点,焦点在坐标轴上,且过两点(4,0),(0,2)的椭圆方程为( )
A.+=1 B.+=1
C.+=1 D.+=1
2.已知双曲线+=1的焦点在x轴上,若该双曲线的焦距为4,则a等于( )
A.1 B.
C.4 D.10
3.若双曲线与椭圆+=1有相同的焦点,它的一条渐近线方程为y=-x,则双曲线的方程为( )
A.y2-x2=96 B.y2-x2=160
C.y2-x2=80 D.y2-x2=24
4.已知动点M的坐标满足方程5=|3x+4y-12|,则动点M的轨迹是( )
A.椭圆 B.双曲线
C.抛物线 D.圆
5.已知抛物线y2=2px(p>0)的准线与曲线x2+y2-4x-5=0相切,则p的值为( )
A.2 B.1
C. D.
6.由抛物线绕它的对称轴旋转所得到的曲面叫抛物面,用于加热水和食物的太阳灶应用了抛物线的光学性质:一束平行于抛物线轴的光线,经过抛物面的反射集中于它的焦点。用一过抛物线轴的平面截抛物面,将所截得的抛物线放在直角坐标系中,对称轴与x轴重合,顶点与原点重合,如图,若抛物线过点A,平行于对称轴的光线经过点A反射后,反射光线交抛物线于点B,则线段AB的中点到准线的距离为( )
A.2 B.
C. D.
7.已知点P(2,1)在椭圆+=1(a>b>0)上,点M(a,b)为平面上一点,O为坐标原点,则当|OM|取最小值时,椭圆的离心率为( )
A. B.
C. D.
8.已知椭圆C:+=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx-ay+2ab=0相切,则椭圆C的离心率为( )
A. B.
C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.对于曲线C:+=1,下面四个说法中正确的是( )
A.曲线C不可能是椭圆
B.“1
A.双曲线C的渐近线方程为y=±x
B.以F1F2为直径的圆的方程为x2+y2=1
C.点P的横坐标为±1
D.△PF1F2的面积为
11.已知双曲线C过点且渐近线为y=±x,则下列结论正确的是( )
A.C的方程为-y2=1
B.C的离心率为
C.曲线y=ex-2-1经过C的一个焦点
D.直线x-y-1=0与C有两个公共点
12.已知抛物线y2=2px(p>0)的焦点为F,过F的直线l交抛物线于A(x1,y1),B(x2,y2)两点(点A在第一象限),则下列结论中正确的是( )
A.x1x2=
B.+=
C.若直线l的倾斜角为,则=3
D.若直线l的倾斜角为,则|AB|=4p
三、填空题:本题共4小题,每小题5分,共20分。把答案填在题中横线上。
13.已知椭圆的短半轴长为1,离心率0
15.已知动点M与两定点A(-1,0),B(1,0)构成△MAB,且直线MA,MB的斜率之积为4。设动点M的轨迹为C,则轨迹C的方程为______________。
16.已知点M和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°,则k=________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)
已知椭圆中心在坐标原点,焦点在x轴上,椭圆与x轴的一个交点到两焦点的距离分别为3和1,求椭圆的标准方程.
18.(本小题满分12分)
已知抛物线y2=2x的焦点为F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求此时P点的坐标.
19.(本小题满分12分)
若方程+=-1表示焦点在y轴上的双曲线,求它的半焦距c的取值范围.
20.(本小题满分12分)
已知椭圆C的中心在原点,一个焦点为F(-2,0),且长轴长与短轴长的比是2∶.
(1)求椭圆C的方程.
(2)设点M(m,0)在椭圆C的长轴上,点P是椭圆上任意一点.当最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
21.(本小题满分12分)
已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3.
(1)求抛物线E的方程;
(2)已知点G(-1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
22.(本小题满分12分)
已知双曲线C:-=1(a>0,b>0)的离心率为,虚轴长为4.
(1)求双曲线的标准方程.
(2)过点(0,1),倾斜角为45°的直线l与双曲线C相交于A,B两点,O为坐标原点,求△OAB的面积.
参考答案
1解析 解法一:验证排除,将点(4,0)代入验证可排除A,B,C。故选D。
解法二:设椭圆方程为mx2+ny2=1(m>0,n>0,m≠n),则解得故选D。
答案 D
2解析 根据题意可知,双曲线的标准方程为-=1。由双曲线的焦距为4,得c=2,则有c2=a-3+a-1=4,解得a=4。
答案 C
3解析 设双曲线方程为x2-y2=λ(λ≠0),因为双曲线与椭圆有相同的焦点,且焦点为(0,±4),所以λ<0,且-2λ=(4)2,得λ=-24。故选D。
答案 D
4解析 方程5=|3x+4y-12|可化为=,它表示点M到坐标原点O的距离等于它到直线3x+4y-12=0的距离,由抛物线的定义,可知动点M的轨迹是抛物线。故选C。
答案 C
5解析 曲线的方程可化为(x-2)2+y2=9,其表示圆心为(2,0),半径为3的圆,又抛物线的准线方程为x=-,所以由抛物线的准线与圆相切得2+=3。解得p=2。
答案 A
6解析 设抛物线方程为y2=2px,将点A代入可得1=2p×,解得p=2,所以抛物线方程为y2=4x,焦点为F(1,0),准线为x=-1。由题意可得,直线AB的方程为y-0=(x-1),即y=-(x-1),由可得y2+3y-4=0,解得或所以A,B(4,-4),可得AB的中点为,所以线段AB的中点到准线的距离为+1=。故选C。
答案 C
7解析 点P(2,1)在椭圆+=1(a>b>0)上,可得+=1,M(a,b)为平面上一点,O为坐标原点,则|OM|==≥=3,当且仅当a2=2b2时,等号成立,此时由解得a2=6,b2=3。所以e===。故选C。
答案 C
8解析 以线段A1A2为直径的圆的方程为x2+y2=a2,因为圆与直线bx-ay+2ab=0相切,所以=a,即2b=,所以a2=3b2。因为a2=b2+c2,所以c2=2b2,所以=,所以e==。故选A。
答案 A
9解析 A项,当1
10解析 等轴双曲线C:y2-x2=1的渐近线方程为y=±x,故A正确。由双曲线的方程可知|F1F2|=2,所以以F1F2为直径的圆的方程为x2+y2=2,故B错误。点P(x0,y0)在圆x2+y2=2上,不妨设点P(x0,y0)在直线y=x上,所以解得|x0|=1,则点P的横坐标为±1,故C正确。由上述分析可得△PF1F2的面积为×2×1=,故D正确。故选ACD。
答案 ACD
11解析 对于选项A:由已知y=±x,可得y2=x2,从而设所求双曲线方程为x2-y2=λ,又由双曲线C过点,从而×32-()2=λ,即λ=1,从而选项A正确;对于选项B:由双曲线方程可知a=,b=1,c=2,从而离心率为e===,所以B选项错误;对于选项C:双曲线的右焦点坐标为,满足y=ex-2-1,从而选项C正确;对于选项D:联立,
整理,得y2-2y+2=0,由Δ=(2)2-4×2=0,知直线与双曲线C只有一个交点,选项D错误.
答案 AC
12解析 抛物线y2=2px(p>0)的焦点为F,准线为x=-,当斜率不存在时,则过焦点的直线的方程为x=,则,B,此时x1x2=,+=+=,故B错误;当斜率存在时,设过焦点的直线方程为y=,联立直线与抛物线方程得消去y得k2x2-(k2p+2p)x+=0,由根与系数的关系可得x1x2=,x1+x2=,故A正确;若直线l的倾斜角为,则k=,所以x1+x2==7p,所以|AB|=x1+x2+p=8p,故D错误;过A,B分别作准线的垂线,垂足分别为M,N,作BE⊥AM,垂足为E,设|AF|=m,=n,则由抛物线的定义得=|AF|=m,|BN|=|BF|=n,|AB|=m+n,|AE|=m-n,因为∠EAB=60°,于是=,解得m=3n,则==3,故C正确。综上,正确的有AC。
答案 AC
13解析 因为b=1,所以c2=a2-1。又==1-≤。所以≥,即a2≤4。又a2-1>0,所以a2>1,故1
14解析 抛物线方程化为y2=-x,所以抛物线开口向左,2p=,=,故焦点坐标为。
答案
15解析 设点M的坐标为(x,y),当x=-1时,直线MA的斜率不存在;当x=1时,直线MB的斜率不存在。于是x≠1且x≠-1。此时,直线MA的斜率为,直线MB的斜率为。由题意有·=4,化简得x2-=1,因为x≠1且x≠-1,即y≠0,所以轨迹C的方程为x2-=1(y≠0)。
答案 x2-=1(y≠0)
16解析 由抛物线的方程y2=4x可知其焦点F的坐标为(1,0),所以直线AB的方程为y=k(x-1),由得k2x2-2(k2+2)x+k2=0,设A(x1,y1),B(x2,y2),所以x1+x2=,x1x2=1,因为∠AMB=90°,所以·=(x1+1,y1-1)·(x2+1,y2-1)=(x1+1)(x2+1)+(y1-1)(y2-1)=(x1+1)(x2+1)+[k(x1-1)-1]·[k(x2-1)-1]=(1-k-k2)(x1+x2)+(1+k2)x1x2+k2+2k+2
=(1-k-k2)+(1+k2)+k2+2k+2=0,
整理可解得k=2.
答案:2
17解析 由题意可得所以
故b2=a2-c2=3,所以椭圆方程为+=1.
18解析 将x=3代入抛物线方程y2=2x,得y=±.因为>2,所以A在抛物线内部.设抛物线上动点P到准线l:x=-的距离为d,由抛物线的定义,知|PA|+|PF|=|PA|+d.当PA⊥l时,|PA|+d最小,最小值为,即|PA|+|PF|的最小值为,此时P点的纵坐标为2,代入y2=2x,得x=2,所以P点的坐标为(2,2).
19解析 因为方程+=-1两边除以-1,方程可化简为-=1,又因为方程表示为焦点在y轴上的双曲线,
所以k-2>0,-3>0即k>3,从而方程可表示为-=1,由于c2=a2+b2=2k-5>1,所以半焦距c的取值范围为c>1,即c∈.
20解析 (1)由题意知解得所以椭圆C的方程为+=1.
(2)设P(x0,y0),且 eq \f(x,16) + eq \f(y,12) =1,所以2=(x0-m)2+y=x-2mx0+m2+12 eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(x,16))) =x-2mx0+m2+12=(x0-4m)2-3m2+12.所以2为关于x0的二次函数,开口向上,对称轴为4m.由题意知,当x0=4时,2最小,所以4m≥4,所以m≥1.又点M(m,0)在椭圆长轴上,所以1≤m≤4.
21解析 (1)由抛物线的定义,得|AF|=2+.因为|AF|=3,即2+=3,解得p=2,所以抛物线E的方程为y2=4x.
(2)因为点A(2,m)在抛物线E:y2=4x上,所以m=±2,由抛物线的对称性,不妨设 A(2,2).由A(2,2),F(1,0)可得,直线AF的方程为y=2(x-1).由,得2x2-5x+2=0,解得x=2或x=,从而B.又G(-1,0),所以kGA==,kGB==-,
所以kGA+kGB=0,从而∠AGF=∠BGF,这表明点F到直线GA,GB的距离相等,故以F为圆心且与直线GA相切的圆必与直线GB相切.
22解析 (1)依题意可得解得a=1,b=2,c=,
所以双曲线的标准方程为x2-=1.
(2)直线l的方程为y=x+1,联立消去y得3x2-2x-5=0,设A(x1,y1),B(x2,y2)由根与系数的关系可得x1+x2=,x1x2=-,则|AB|=|x1-x2|==×=,原点到直线l的距离为d=,所以S△OAB=·|AB|·d=××=.所以△OAB的面积为.
