人教版九年级数学上册23.2.3《关于原点对称的点的坐标》教学方案(表格式)
文档属性
| 名称 | 人教版九年级数学上册23.2.3《关于原点对称的点的坐标》教学方案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 365.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 11:29:52 | ||
图片预览


文档简介
第二十三章 旋转
23.2.3关于原点对称的点的坐标
一、 教学目标
1.能够正确认识关于原点对称的两点的坐标间的关系.
2.能够运用关于原点对称的两点的坐标间的关系,在平面直角坐标系中作图.
3.经历了观察、交流、归纳等过程,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力.
4.通过学习平面直角坐标系内点的坐标对称的关系,培养学生善于归纳类比的学习精神.二、 教学重难点
重点:探究关于原点对称的点的坐标的规律.
难点:关于原点对称的点的坐标的规律及其运用.
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
教学目标 【学习目标】 1.能够正确认识关于原点对称的两点的坐标间的关系. 2.能够运用关于原点对称的两点的坐标间的关系,在平面直角坐标系中作图. 3.经历了观察、交流、归纳等过程,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力. 4.通过学习平面直角坐标系内点的坐标对称的关系,培养学生善于归纳类比的学习精神. 熟悉学习目标 通过学习目标让学生熟悉本节课要讲解的内容.
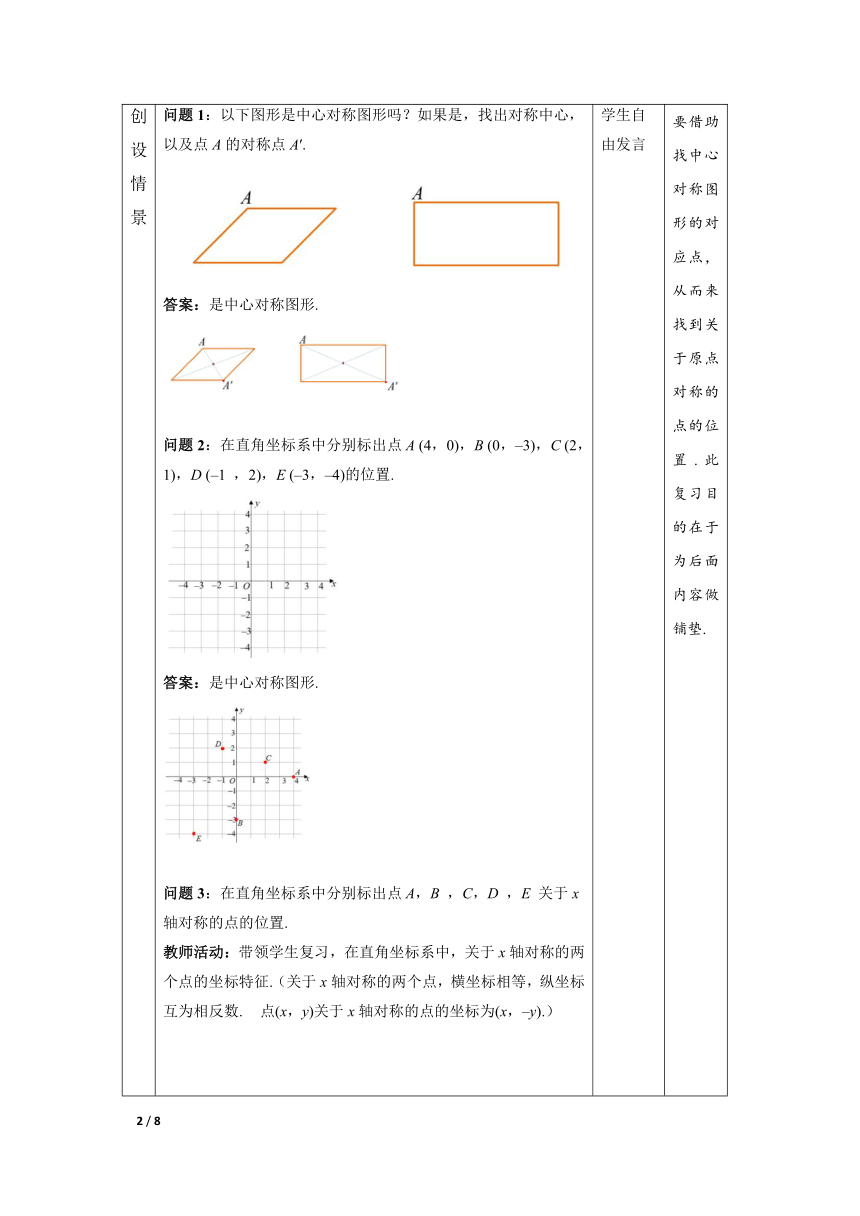
环节一 创设情景 【回顾旧知】 教师活动:引领学生们一起识别中心对称图形和中心对称图形的对应点. 问题1:以下图形是中心对称图形吗?如果是,找出对称中心,以及点A的对称点A′. 答案:是中心对称图形. 问题2:在直角坐标系中分别标出点A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4)的位置. 答案:是中心对称图形. 问题3:在直角坐标系中分别标出点A,B ,C,D ,E 关于x轴对称的点的位置. 教师活动:带领学生复习,在直角坐标系中,关于x轴对称的两个点的坐标特征.(关于x轴对称的两个点,横坐标相等,纵坐标互为相反数. 点(x,y)关于x轴对称的点的坐标为(x,–y).) 答案: 问题4:在直角坐标系中分别标出点A,B ,C,D ,E 关于y轴对称的点的位置. 教师活动:带领学生复习,在直角坐标系中,关于y轴对称的两个点的坐标特征.(关于y轴对称的两个点,横坐标互为相反数,纵坐标相等. 点(x,y)关于x轴对称的点的坐标为(–x, y).) 答案: 学生自由发言 后面内容的讲解,需要借助找中心对称图形的对应点,从而来找到关于原点对称的点的位置.此复习目的在于为后面内容做铺垫. 复习与本节课相关内容,培养学生类比的思想方法,为后面的探究做铺垫.
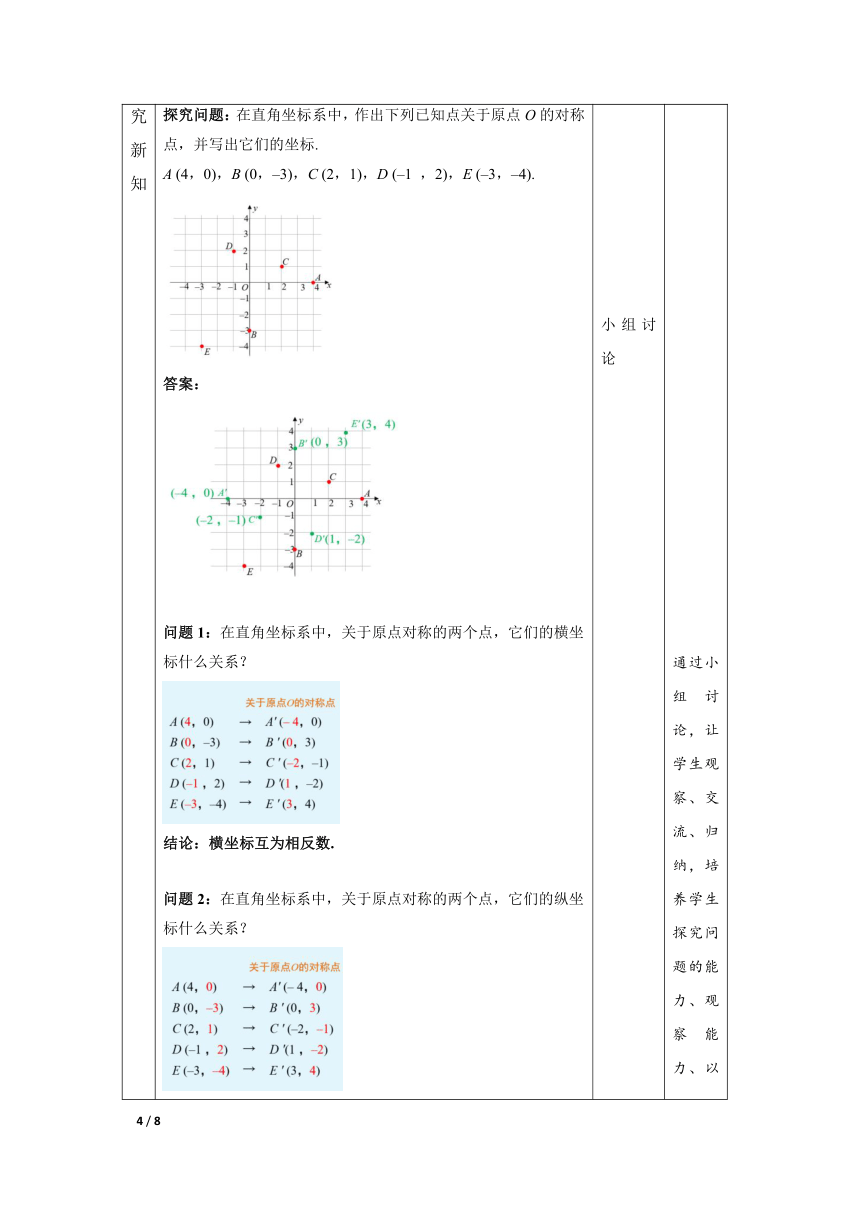
环节二探究新知 【探究】 教师活动:教师给学生时间讨论点的位置,在找点C、D、E关于原点对称的点时,学生会迷惑,可借助长方形一条对角线的两个端点为一组对称点来解决.然后依次提出两个问题,引导学生观察、思考,归纳,总结出结论. 探究问题:在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标. A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4). 答案: 问题1:在直角坐标系中,关于原点对称的两个点,它们的横坐标什么关系? 结论:横坐标互为相反数. 问题2:在直角坐标系中,关于原点对称的两个点,它们的纵坐标什么关系? 结论:纵坐标互为相反数. 【归纳】 P(x,y)关于原点O的对称点P′ (–x,–y). P(x,y)关于x轴的对称点P′ (–x,–y). P(x,y)关于y轴的对称点P′ (–x,–y). 【做一做】 1. 写出下列各点关于原点的对称点的坐标: (1)点A(3,1)关于原点对称的点的坐标A′( , ); (2)点B( – 2 ,3)关于原点对称的点的坐标B′( , ); (3)点C( – 1, – 2)关于原点对称的点的坐标C′( , ); (3)点D( 2, – 3)关于原点对称的点的坐标C′( , ). 答案: (1) –3; –1 (2) 2; –3 (3) 1; 2 (4) –2; 3. 2. 下列各点中哪两个点关于原点对称? A(–5,0)、B(0,2)、C(2,–1)、D(2,0)、E(0,5)、 F(–2,1)、G (–2,–1). 答案:解:C(2,–1)与 F(–2,1)关于原点对称. 小组讨论 集体回答 通过小组讨论,让学生观察、交流、归纳,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力. 做练习,及时巩固知识,了解学生知识的掌握程度.
环节三应用新知 【典型例题】 例:如图所示,利用关于原点对称的点的坐标的关系,作出与△ABC 关于原点对称的图形. 答案: 解:点P(x,y) 关于原点的对称点为P′(–x,–y),△ABC 的三个顶点A(–4,1),B(–1,–1),C(–3,2),关于原点的对称点分别为 A′(4,–1),B′(1,1),C′(3,–2),依次连接A′B′,B′C′,C′A′,就可得到与△ABC 关于原点对称的△A′B′C′. 【归纳】 在直角坐标系中,画一个图形关于原点对称的图形的一般步骤: 1. 确定关键点(通常为图形顶点等特殊点)的坐标. 2. 求出关键点关于原点的对称点的坐标,并在直角坐标系中标出. 3. 顺次连接对称点,组成的图形为所求. 运用关于原点对称的两点的坐标间的关系,使学生掌握在平面直角坐标系中作图的方法.
环节四 巩固新知 【随堂练习】 练习1 填空: 若设点M(a,b), 点M关于x轴的对称点M1 ( , ); 点M关于y轴的对称点M2 ( , ); 点M关于O轴的对称点M3 ( , ). 答案:(1)a,–b (2) –a,b (3) –a,–b. 练习2 填空: 已知点A(–1, – 3), 关于x轴对称的点的坐标是_________; 关于y轴对称的点的坐标是_________; 关于原点对称的点的坐标是________. 答案:(–1,3),(1, –3),(1,3). 练习3 填空: 点A(m, – 2), B(1, n)关于x轴对称,则m=____,n=____. 点A(m, – 2), B(1, n)关于y轴对称,则m=_____,n=_____. 点A(m, – 2), B(1, n)关于原点对称,则m=_____,n=_____. 答案: 1,2; –1,–2; –1,2. 练习4 在如图所示编号为①、②、③、④的四个三角形中,关于x轴对称的两个三角形的编号为_________;关于y轴对称的两个三角形的编号为_________;关于原点O对称的两个三角形的编号为__________. 答案: ①与③; ①与②; ②与③. 独立做题 进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 巩固例题练习 教科书第69页,练习3. 第70页,习题3、4. 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
9 / 9
23.2.3关于原点对称的点的坐标
一、 教学目标
1.能够正确认识关于原点对称的两点的坐标间的关系.
2.能够运用关于原点对称的两点的坐标间的关系,在平面直角坐标系中作图.
3.经历了观察、交流、归纳等过程,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力.
4.通过学习平面直角坐标系内点的坐标对称的关系,培养学生善于归纳类比的学习精神.二、 教学重难点
重点:探究关于原点对称的点的坐标的规律.
难点:关于原点对称的点的坐标的规律及其运用.
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
教学目标 【学习目标】 1.能够正确认识关于原点对称的两点的坐标间的关系. 2.能够运用关于原点对称的两点的坐标间的关系,在平面直角坐标系中作图. 3.经历了观察、交流、归纳等过程,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力. 4.通过学习平面直角坐标系内点的坐标对称的关系,培养学生善于归纳类比的学习精神. 熟悉学习目标 通过学习目标让学生熟悉本节课要讲解的内容.
环节一 创设情景 【回顾旧知】 教师活动:引领学生们一起识别中心对称图形和中心对称图形的对应点. 问题1:以下图形是中心对称图形吗?如果是,找出对称中心,以及点A的对称点A′. 答案:是中心对称图形. 问题2:在直角坐标系中分别标出点A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4)的位置. 答案:是中心对称图形. 问题3:在直角坐标系中分别标出点A,B ,C,D ,E 关于x轴对称的点的位置. 教师活动:带领学生复习,在直角坐标系中,关于x轴对称的两个点的坐标特征.(关于x轴对称的两个点,横坐标相等,纵坐标互为相反数. 点(x,y)关于x轴对称的点的坐标为(x,–y).) 答案: 问题4:在直角坐标系中分别标出点A,B ,C,D ,E 关于y轴对称的点的位置. 教师活动:带领学生复习,在直角坐标系中,关于y轴对称的两个点的坐标特征.(关于y轴对称的两个点,横坐标互为相反数,纵坐标相等. 点(x,y)关于x轴对称的点的坐标为(–x, y).) 答案: 学生自由发言 后面内容的讲解,需要借助找中心对称图形的对应点,从而来找到关于原点对称的点的位置.此复习目的在于为后面内容做铺垫. 复习与本节课相关内容,培养学生类比的思想方法,为后面的探究做铺垫.
环节二探究新知 【探究】 教师活动:教师给学生时间讨论点的位置,在找点C、D、E关于原点对称的点时,学生会迷惑,可借助长方形一条对角线的两个端点为一组对称点来解决.然后依次提出两个问题,引导学生观察、思考,归纳,总结出结论. 探究问题:在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标. A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4). 答案: 问题1:在直角坐标系中,关于原点对称的两个点,它们的横坐标什么关系? 结论:横坐标互为相反数. 问题2:在直角坐标系中,关于原点对称的两个点,它们的纵坐标什么关系? 结论:纵坐标互为相反数. 【归纳】 P(x,y)关于原点O的对称点P′ (–x,–y). P(x,y)关于x轴的对称点P′ (–x,–y). P(x,y)关于y轴的对称点P′ (–x,–y). 【做一做】 1. 写出下列各点关于原点的对称点的坐标: (1)点A(3,1)关于原点对称的点的坐标A′( , ); (2)点B( – 2 ,3)关于原点对称的点的坐标B′( , ); (3)点C( – 1, – 2)关于原点对称的点的坐标C′( , ); (3)点D( 2, – 3)关于原点对称的点的坐标C′( , ). 答案: (1) –3; –1 (2) 2; –3 (3) 1; 2 (4) –2; 3. 2. 下列各点中哪两个点关于原点对称? A(–5,0)、B(0,2)、C(2,–1)、D(2,0)、E(0,5)、 F(–2,1)、G (–2,–1). 答案:解:C(2,–1)与 F(–2,1)关于原点对称. 小组讨论 集体回答 通过小组讨论,让学生观察、交流、归纳,培养学生探究问题的能力、观察能力、以及与他人合作交流的能力. 做练习,及时巩固知识,了解学生知识的掌握程度.
环节三应用新知 【典型例题】 例:如图所示,利用关于原点对称的点的坐标的关系,作出与△ABC 关于原点对称的图形. 答案: 解:点P(x,y) 关于原点的对称点为P′(–x,–y),△ABC 的三个顶点A(–4,1),B(–1,–1),C(–3,2),关于原点的对称点分别为 A′(4,–1),B′(1,1),C′(3,–2),依次连接A′B′,B′C′,C′A′,就可得到与△ABC 关于原点对称的△A′B′C′. 【归纳】 在直角坐标系中,画一个图形关于原点对称的图形的一般步骤: 1. 确定关键点(通常为图形顶点等特殊点)的坐标. 2. 求出关键点关于原点的对称点的坐标,并在直角坐标系中标出. 3. 顺次连接对称点,组成的图形为所求. 运用关于原点对称的两点的坐标间的关系,使学生掌握在平面直角坐标系中作图的方法.
环节四 巩固新知 【随堂练习】 练习1 填空: 若设点M(a,b), 点M关于x轴的对称点M1 ( , ); 点M关于y轴的对称点M2 ( , ); 点M关于O轴的对称点M3 ( , ). 答案:(1)a,–b (2) –a,b (3) –a,–b. 练习2 填空: 已知点A(–1, – 3), 关于x轴对称的点的坐标是_________; 关于y轴对称的点的坐标是_________; 关于原点对称的点的坐标是________. 答案:(–1,3),(1, –3),(1,3). 练习3 填空: 点A(m, – 2), B(1, n)关于x轴对称,则m=____,n=____. 点A(m, – 2), B(1, n)关于y轴对称,则m=_____,n=_____. 点A(m, – 2), B(1, n)关于原点对称,则m=_____,n=_____. 答案: 1,2; –1,–2; –1,2. 练习4 在如图所示编号为①、②、③、④的四个三角形中,关于x轴对称的两个三角形的编号为_________;关于y轴对称的两个三角形的编号为_________;关于原点O对称的两个三角形的编号为__________. 答案: ①与③; ①与②; ②与③. 独立做题 进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 巩固例题练习 教科书第69页,练习3. 第70页,习题3、4. 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
9 / 9
同课章节目录
