人教版九年级数学上册24.1 圆的有关性质24.1.4 圆周角 教案(表格式)
文档属性
| 名称 | 人教版九年级数学上册24.1 圆的有关性质24.1.4 圆周角 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 488.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 11:11:36 | ||
图片预览



文档简介
第二十四章 圆
圆的有关性质
24.1.4 圆周角
第1课时 圆周角
一、教学目标
1.了解圆周角的概念,会证明圆周角定理及其推论;
2.初步运用圆周角定理进行证明和计算;
3.经历圆周角定理的发现、探究与证明,使学生感悟分类讨论的数学思想,体会数学知识的一般形成过程;
4.通过学生自主探究圆周角的概念及定理,合作交流的学习过程,体验实现自身价值的愉悦和数学的应用.
二、教学重难点
重点:圆周角定理.
难点:运用分类讨论思想证明圆周角定理.
三、教学用具
多媒体课件
四、教学过程设计
教学环节 教师活动 学生活动 设计意图
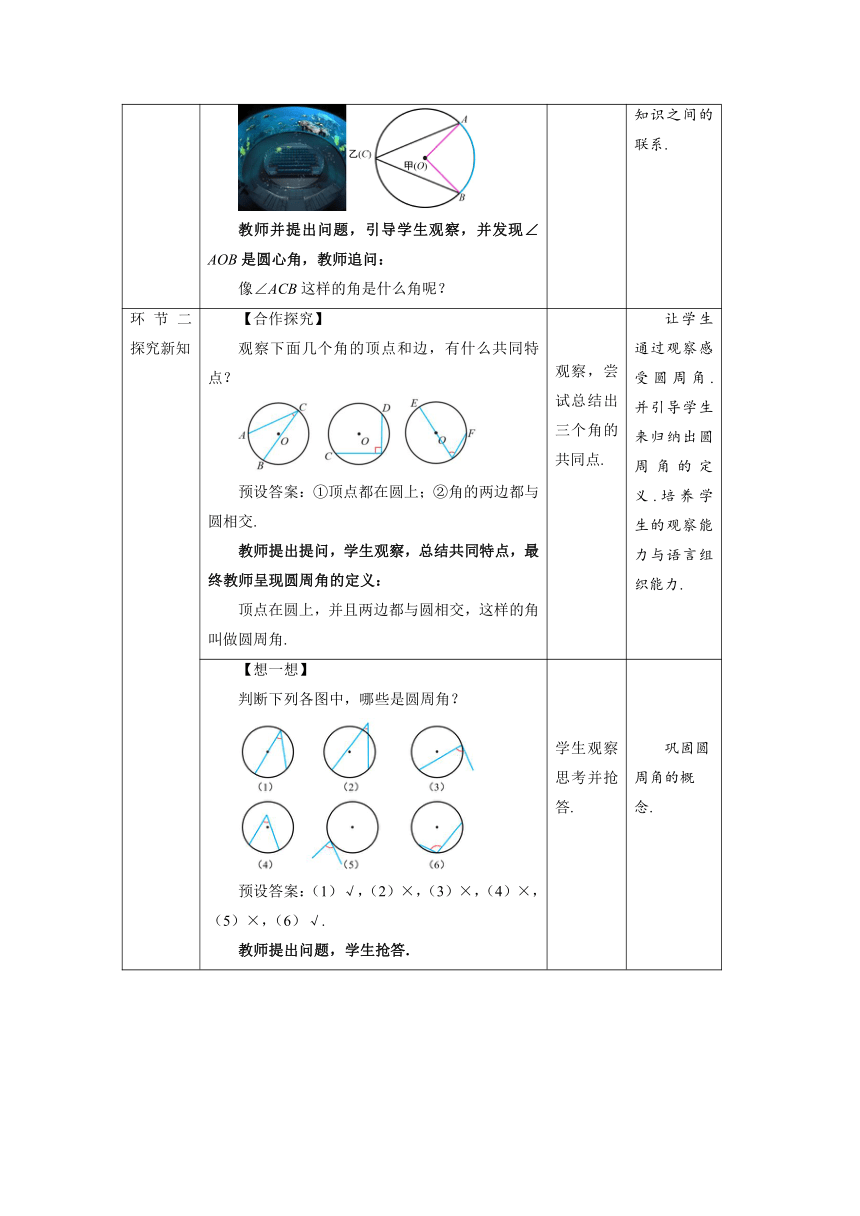
环节一 创设情境 【观察思考】 在海洋馆例,人们可以通过圆弧形玻璃观看其中的海洋动物.如图,为圆弧形玻璃窗,甲站在圆心O的位置,乙站在正对着玻璃窗的靠墙的位置C,它们的视角∠AOB和∠ACB的顶点和边有哪些特点? 教师并提出问题,引导学生观察,并发现∠AOB是圆心角,教师追问: 像∠ACB这样的角是什么角呢? 观察图片,根据老师的提问,思考. 通过实际情境引入,先回顾已学知识,在此基础上提出问题,引导学生思考新知识,建立起新旧知识之间的联系.
环节二 探究新知 【合作探究】 观察下面几个角的顶点和边,有什么共同特点? 预设答案:①顶点都在圆上;②角的两边都与圆相交. 教师提出提问,学生观察,总结共同特点,最终教师呈现圆周角的定义: 顶点在圆上,并且两边都与圆相交,这样的角叫做圆周角. 观察,尝试总结出三个角的共同点. 让学生通过观察感受圆周角.并引导学生来归纳出圆周角的定义.培养学生的观察能力与语言组织能力.
【想一想】 判断下列各图中,哪些是圆周角? 预设答案:(1)√,(2)×,(3)×,(4)×,(5)×,(6)√. 教师提出问题,学生抢答. 学生观察思考并抢答. 巩固圆周角的概念.
【思考】 创设情境的问题中,甲乙两人的视角∠AOB和∠ACB的大小有什么关系? 预设答案: 教师提出问题,让学生动手测量,发现这两个角之间的关系. 追问1:在⊙O中任取一条弧,分别测量这条弧所对的圆心角和圆周角,你还能得到前面的结论吗? 教师组织小组合作,让学生动手画图、测量,观察结果并总结规律,教师巡视,如遇到有困难的学生适当提示,最终教师PPT呈现结论. 同弧所对的圆周角度数等于这条弧所对圆心角的一半. 追问2:如何证明这个结论呢? 教师提出问题后,先让学生在圆中画出同弧所对的圆心角和圆周角,引导学生观察圆心与圆周角位置,发现有3类情况: 1.圆心在圆周角的一边上,如图(1); 2.圆心在圆周角的内部,如图(2); 3.圆心在圆周角的外部,如图(3). 学生观察,用量角器测量,思考并回答. 通过观察、猜想、测量验证的过程,引导学生发现圆周角定理.让学生参与到圆周角定理的发现过程,充分体现学生的主体作用.
【证明】 在第(1)种情况下,如何证明? 预设答案:∵OAOC,∴∠A∠C 又∵∠BOC∠A∠C ∴ 教师提出问题,带领学生分析第(1)种情况的证明思路,然后让学生自行完成第(2)、(3)种情况的证明,最终教师PPT展示.从而得出圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半. 学生自行完成后面两种情况的证明.小组交流后,选代表回答. 通过证明使学生对圆周角定理的认识从感性上升到理性. 培养学生的逻辑思维能力以及分类讨论的数学思想.
【思考】 “在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢? 预设答案:相等. 教师提出问题后,先让学生试着猜想,然后再验证. 证明:连接OB,OC. 由圆周角定理得:,,, ∴∠BAC∠BDC∠BEC 追问:等弧所对的圆周角呢?相等吗? 教师提出问题,学生仿照前面的思路证明,教师PPT展示过程. 证明:连接OA、OB、OC、OD; ∵ ,∴∠AOC∠BOD 又∵, ∴∠ADC∠BAD 从而得到圆周角定理的推论: 同弧或等弧所对的圆周角相等. 学生思考并证明. 让学生经历观察、猜想、证明得出推论的探索过程,得到圆周角定理的推论,进一步认识与圆有关的角和弧之间的关系
【做一做】 如图,AB是直径,C是圆上任意一点(不与A、B重合),求∠ACB °. 预设答案:90. 教师提出问题,学生应用所学知识作答.在学生得到结果后,教师追问: 如果∠ACB90°,能得出AB是直径吗? 预设答案:能. 从而得到圆周角定理的另一个推论: 半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 学生思考并作答. 由一般到特殊进一步认识定理,加深对定理的理解,获得推论.
【归纳】 教师带领学生系统梳理圆周角定理及其推论. 学生回顾,尝试用自己的语言复述. 梳理本节课的重点内容,加深对圆周角定理及其推论的理解.
环节三 应用新知 【典型例题】 教师提出问题,学生先独立思考,解答.然后再小组交流探讨,教师巡视,如遇到有困难的学生适当点拨,最终教师展示答题过程. 例1 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长. 解:连接OD,∵AB是直径 ∴∠ACB=∠ADB=90°. 在Rt△ABC中, 又∵CD平分∠ACB,∴∠ACD∠BCD ∴ADBD 在Rt△ABD中,AD2BD2AB2 ∴ADBDAB10 学生观察、思考并回答. 应用圆周角定理及推论解决问题,巩固所学的内容.
环节四 巩固新知 教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解. 1.如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=___. 答:50° 2.在⊙O中,∠CBD=30°,∠BDC=20°,求∠A. 解:方法一:连接AC ∠CAD=∠CBD=30° ∠BAC=∠BDC=20° ∠A∠CAD∠BAC=50° 方法二:连接OB,OC,OD. ∠BOC=2∠BDC=40° ∠COD=2∠CBD=60° ∠BOD∠BOC∠COD=100° 3.如图,在⊙O中,AB为直径,,弦CG⊥AB,交AB于D,交BF于E.求证:BE=EC. 证明:连接CB, ∵AB为直径,弦CG⊥AB, ∴ 又∵ ∴ ∴∠CBF=∠BCG ∴ BE=EC 学生自主练习 进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
环节五 课堂小结 思维导图的形式呈现本节课的主要内容: 学生回顾本节课所学知识,谈收获,体会,师评价. 通过提问让学生回顾、总结、梳理本节课所学内容. 使零散的知识系统化,同时培养学生的语言表达能力.
环节六 布置作业 教科书第88页练习第1、3题. 学生课后自主完成. 通过作业,反馈对所学知识的掌握程度.
圆的有关性质
24.1.4 圆周角
第1课时 圆周角
一、教学目标
1.了解圆周角的概念,会证明圆周角定理及其推论;
2.初步运用圆周角定理进行证明和计算;
3.经历圆周角定理的发现、探究与证明,使学生感悟分类讨论的数学思想,体会数学知识的一般形成过程;
4.通过学生自主探究圆周角的概念及定理,合作交流的学习过程,体验实现自身价值的愉悦和数学的应用.
二、教学重难点
重点:圆周角定理.
难点:运用分类讨论思想证明圆周角定理.
三、教学用具
多媒体课件
四、教学过程设计
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 【观察思考】 在海洋馆例,人们可以通过圆弧形玻璃观看其中的海洋动物.如图,为圆弧形玻璃窗,甲站在圆心O的位置,乙站在正对着玻璃窗的靠墙的位置C,它们的视角∠AOB和∠ACB的顶点和边有哪些特点? 教师并提出问题,引导学生观察,并发现∠AOB是圆心角,教师追问: 像∠ACB这样的角是什么角呢? 观察图片,根据老师的提问,思考. 通过实际情境引入,先回顾已学知识,在此基础上提出问题,引导学生思考新知识,建立起新旧知识之间的联系.
环节二 探究新知 【合作探究】 观察下面几个角的顶点和边,有什么共同特点? 预设答案:①顶点都在圆上;②角的两边都与圆相交. 教师提出提问,学生观察,总结共同特点,最终教师呈现圆周角的定义: 顶点在圆上,并且两边都与圆相交,这样的角叫做圆周角. 观察,尝试总结出三个角的共同点. 让学生通过观察感受圆周角.并引导学生来归纳出圆周角的定义.培养学生的观察能力与语言组织能力.
【想一想】 判断下列各图中,哪些是圆周角? 预设答案:(1)√,(2)×,(3)×,(4)×,(5)×,(6)√. 教师提出问题,学生抢答. 学生观察思考并抢答. 巩固圆周角的概念.
【思考】 创设情境的问题中,甲乙两人的视角∠AOB和∠ACB的大小有什么关系? 预设答案: 教师提出问题,让学生动手测量,发现这两个角之间的关系. 追问1:在⊙O中任取一条弧,分别测量这条弧所对的圆心角和圆周角,你还能得到前面的结论吗? 教师组织小组合作,让学生动手画图、测量,观察结果并总结规律,教师巡视,如遇到有困难的学生适当提示,最终教师PPT呈现结论. 同弧所对的圆周角度数等于这条弧所对圆心角的一半. 追问2:如何证明这个结论呢? 教师提出问题后,先让学生在圆中画出同弧所对的圆心角和圆周角,引导学生观察圆心与圆周角位置,发现有3类情况: 1.圆心在圆周角的一边上,如图(1); 2.圆心在圆周角的内部,如图(2); 3.圆心在圆周角的外部,如图(3). 学生观察,用量角器测量,思考并回答. 通过观察、猜想、测量验证的过程,引导学生发现圆周角定理.让学生参与到圆周角定理的发现过程,充分体现学生的主体作用.
【证明】 在第(1)种情况下,如何证明? 预设答案:∵OAOC,∴∠A∠C 又∵∠BOC∠A∠C ∴ 教师提出问题,带领学生分析第(1)种情况的证明思路,然后让学生自行完成第(2)、(3)种情况的证明,最终教师PPT展示.从而得出圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半. 学生自行完成后面两种情况的证明.小组交流后,选代表回答. 通过证明使学生对圆周角定理的认识从感性上升到理性. 培养学生的逻辑思维能力以及分类讨论的数学思想.
【思考】 “在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢? 预设答案:相等. 教师提出问题后,先让学生试着猜想,然后再验证. 证明:连接OB,OC. 由圆周角定理得:,,, ∴∠BAC∠BDC∠BEC 追问:等弧所对的圆周角呢?相等吗? 教师提出问题,学生仿照前面的思路证明,教师PPT展示过程. 证明:连接OA、OB、OC、OD; ∵ ,∴∠AOC∠BOD 又∵, ∴∠ADC∠BAD 从而得到圆周角定理的推论: 同弧或等弧所对的圆周角相等. 学生思考并证明. 让学生经历观察、猜想、证明得出推论的探索过程,得到圆周角定理的推论,进一步认识与圆有关的角和弧之间的关系
【做一做】 如图,AB是直径,C是圆上任意一点(不与A、B重合),求∠ACB °. 预设答案:90. 教师提出问题,学生应用所学知识作答.在学生得到结果后,教师追问: 如果∠ACB90°,能得出AB是直径吗? 预设答案:能. 从而得到圆周角定理的另一个推论: 半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 学生思考并作答. 由一般到特殊进一步认识定理,加深对定理的理解,获得推论.
【归纳】 教师带领学生系统梳理圆周角定理及其推论. 学生回顾,尝试用自己的语言复述. 梳理本节课的重点内容,加深对圆周角定理及其推论的理解.
环节三 应用新知 【典型例题】 教师提出问题,学生先独立思考,解答.然后再小组交流探讨,教师巡视,如遇到有困难的学生适当点拨,最终教师展示答题过程. 例1 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长. 解:连接OD,∵AB是直径 ∴∠ACB=∠ADB=90°. 在Rt△ABC中, 又∵CD平分∠ACB,∴∠ACD∠BCD ∴ADBD 在Rt△ABD中,AD2BD2AB2 ∴ADBDAB10 学生观察、思考并回答. 应用圆周角定理及推论解决问题,巩固所学的内容.
环节四 巩固新知 教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解. 1.如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=___. 答:50° 2.在⊙O中,∠CBD=30°,∠BDC=20°,求∠A. 解:方法一:连接AC ∠CAD=∠CBD=30° ∠BAC=∠BDC=20° ∠A∠CAD∠BAC=50° 方法二:连接OB,OC,OD. ∠BOC=2∠BDC=40° ∠COD=2∠CBD=60° ∠BOD∠BOC∠COD=100° 3.如图,在⊙O中,AB为直径,,弦CG⊥AB,交AB于D,交BF于E.求证:BE=EC. 证明:连接CB, ∵AB为直径,弦CG⊥AB, ∴ 又∵ ∴ ∴∠CBF=∠BCG ∴ BE=EC 学生自主练习 进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
环节五 课堂小结 思维导图的形式呈现本节课的主要内容: 学生回顾本节课所学知识,谈收获,体会,师评价. 通过提问让学生回顾、总结、梳理本节课所学内容. 使零散的知识系统化,同时培养学生的语言表达能力.
环节六 布置作业 教科书第88页练习第1、3题. 学生课后自主完成. 通过作业,反馈对所学知识的掌握程度.
同课章节目录
