人教版九年级数学上册22.1.1《二次函数》教学课件(共14张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.1.1《二次函数》教学课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 832.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 11:23:21 | ||
图片预览





文档简介
(共14张PPT)
22.1.1二次函数
学习目标
(1)理解、掌握二次函数的概念和一般形式.
(2)会利用二次函数的概念解决问题.
(3)列二次函数表达式解决实际问题.
(4)了解二次函数在实际问题中的运用价值
重点
二次函数
难点
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
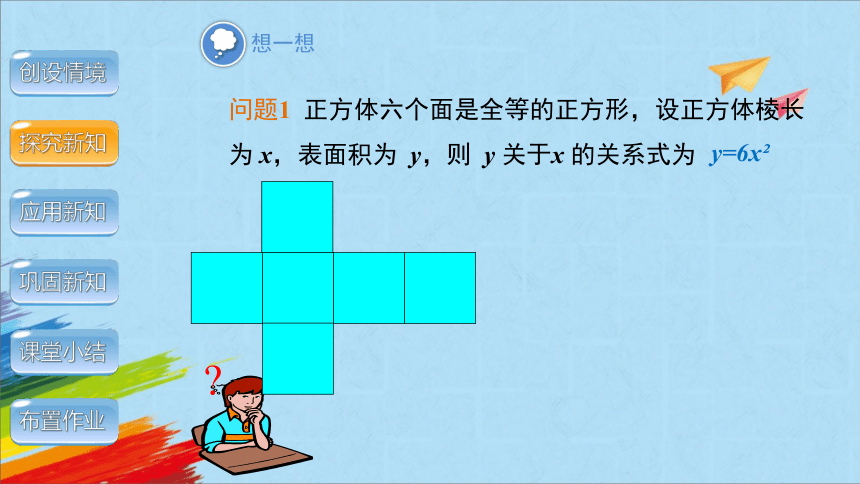
问题1 正方体六个面是全等的正方形,设正方体棱长为 x,表面积为 y,则 y 关于x 的关系式为
y=6x
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
问题2 n个人参加某项活动,每两个人握一次手,这n个人握手的总次数m与人数n有什么关系?
m=即m= -n
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
问题3 某种产品现在的年产量为20t,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的年产量y将随计划所定的x值而确定,y与x之间的关系应该怎样表示
产品原产量
是20t
一年后的产量
再经过一年后的产量
∴两年后的产量y与增加的倍数x的关系式为
20(1+x)t
20(1+x)(1+x)t
y=20(1+x)
即y=20x +40x+20
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
请观察下面三个式子,它们的变量对应关系可用怎样的函数表示?这些函数有什么共同特点?请你结合学习一次函数的经验,给它下个定义.
(1)y=6x
(2) m= -n
(3)y=20x +40x+20
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
二次函数的定义
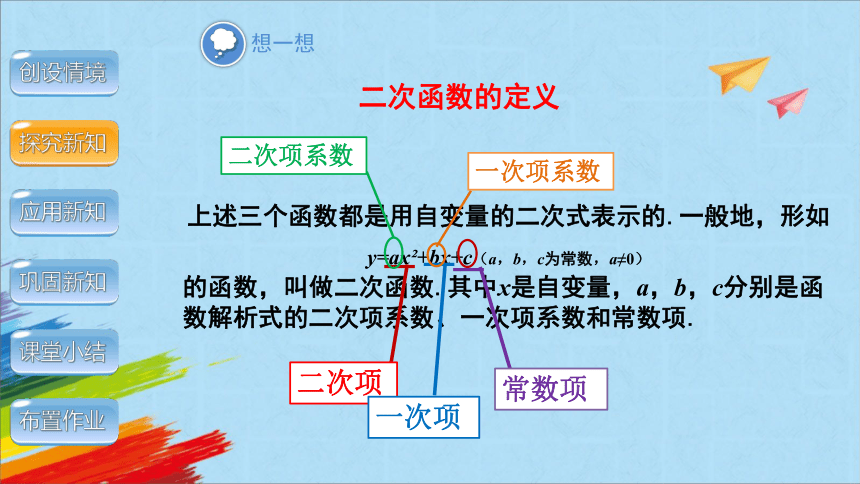
上述三个函数都是用自变量的二次式表示的.一般地,形如y=ax +bx+c(a,b,c为常数,a≠0)
的函数,叫做二次函数.其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
二次项
一次项
常数项
二次项系数
一次项系数
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
(1)二次函数概念中a、b、c有怎样的要求?
(2)当a=0时,这个函数还是二次函数吗?为什么?
(3)b或c能为0吗?
a,b,c为常数,a≠0
不是,有可能是一次函数,当b≠0时,是一次函数;当b=0时,是一个常数函数
当a≠0时,b或c可以为0
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
1.下列函数,哪些是二次函数,哪些不是?
随堂练习
(1)y=3x -2 ( )
(2)m=-n -3 ( )
(3)y=x(1-2x)+2x ( )
(4)y=x(+3x) ( )
(5)y=+x -2 ( )
(6)y=x (1+x ) ( )
判断依据:
y=ax +bx+c(a,b,c为常数,a≠0)
√
√
×
合并后a=0
√
×
×
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.已知y=(m+1)关于x的二次函数,求它的解析式
分析:若y=(m+1)是二次函数,需满足的条件是: =2且m+1≠0
解:由题意可得,
解得,
∴m=2
∴m=2时,函数为二次函数
y=3x
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,在长200米,宽80米的矩形广场内修建等宽的十字形道路,剩余部分为绿地,请写出绿地面积y(m )与路宽x(m)之间的函数关系
思路1:绿地面积=矩形广场面积-等宽的十字形道路面积;思路2:绿地面积等于长为(200-x)m、宽为(80-x)m的新矩形的面积
y=x -280x+16000(0<x<80)
二次函数的图像和性质
定义
运用
应用
会利用二次函数的概念解决问题
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
理解、掌握二次函数的概念和一般形式
列二次函数表达式解决实际问题
布置作业
教科书第29页练习1、2
第41页习题22.1 第1、2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
22.1.1二次函数
学习目标
(1)理解、掌握二次函数的概念和一般形式.
(2)会利用二次函数的概念解决问题.
(3)列二次函数表达式解决实际问题.
(4)了解二次函数在实际问题中的运用价值
重点
二次函数
难点
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
问题1 正方体六个面是全等的正方形,设正方体棱长为 x,表面积为 y,则 y 关于x 的关系式为
y=6x
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
问题2 n个人参加某项活动,每两个人握一次手,这n个人握手的总次数m与人数n有什么关系?
m=即m= -n
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
问题3 某种产品现在的年产量为20t,计划今后两年增加产量。如果每年都比上一年的产量增加x倍,那么两年后这种产品的年产量y将随计划所定的x值而确定,y与x之间的关系应该怎样表示
产品原产量
是20t
一年后的产量
再经过一年后的产量
∴两年后的产量y与增加的倍数x的关系式为
20(1+x)t
20(1+x)(1+x)t
y=20(1+x)
即y=20x +40x+20
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
请观察下面三个式子,它们的变量对应关系可用怎样的函数表示?这些函数有什么共同特点?请你结合学习一次函数的经验,给它下个定义.
(1)y=6x
(2) m= -n
(3)y=20x +40x+20
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
二次函数的定义
上述三个函数都是用自变量的二次式表示的.一般地,形如y=ax +bx+c(a,b,c为常数,a≠0)
的函数,叫做二次函数.其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
二次项
一次项
常数项
二次项系数
一次项系数
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
(1)二次函数概念中a、b、c有怎样的要求?
(2)当a=0时,这个函数还是二次函数吗?为什么?
(3)b或c能为0吗?
a,b,c为常数,a≠0
不是,有可能是一次函数,当b≠0时,是一次函数;当b=0时,是一个常数函数
当a≠0时,b或c可以为0
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
1.下列函数,哪些是二次函数,哪些不是?
随堂练习
(1)y=3x -2 ( )
(2)m=-n -3 ( )
(3)y=x(1-2x)+2x ( )
(4)y=x(+3x) ( )
(5)y=+x -2 ( )
(6)y=x (1+x ) ( )
判断依据:
y=ax +bx+c(a,b,c为常数,a≠0)
√
√
×
合并后a=0
√
×
×
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.已知y=(m+1)关于x的二次函数,求它的解析式
分析:若y=(m+1)是二次函数,需满足的条件是: =2且m+1≠0
解:由题意可得,
解得,
∴m=2
∴m=2时,函数为二次函数
y=3x
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,在长200米,宽80米的矩形广场内修建等宽的十字形道路,剩余部分为绿地,请写出绿地面积y(m )与路宽x(m)之间的函数关系
思路1:绿地面积=矩形广场面积-等宽的十字形道路面积;思路2:绿地面积等于长为(200-x)m、宽为(80-x)m的新矩形的面积
y=x -280x+16000(0<x<80)
二次函数的图像和性质
定义
运用
应用
会利用二次函数的概念解决问题
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
理解、掌握二次函数的概念和一般形式
列二次函数表达式解决实际问题
布置作业
教科书第29页练习1、2
第41页习题22.1 第1、2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
