人教版九年级数学上册24.1.2《垂直于弦的直径》教学课件(共21张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.2《垂直于弦的直径》教学课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 12:15:43 | ||
图片预览


文档简介
(共21张PPT)
24.1.2 垂直于弦的直径
学习目标
1.探索圆的对称性,进而得到垂径定理及其推论;
2.能利用垂径定理及其推论解决相关证明、计算及实际问题;
3.经历探索垂径定理及其推论的过程,发展推理能力,让学生领会数学的严谨性,培养学生实事求是的科学态度;
4.进一步体会和理解研究几何图形的各种方法;培养学生独立探索,相互合作交流的精神,并体验发现的乐趣.
垂直于弦的直径
赵州桥
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
37m
7.23m
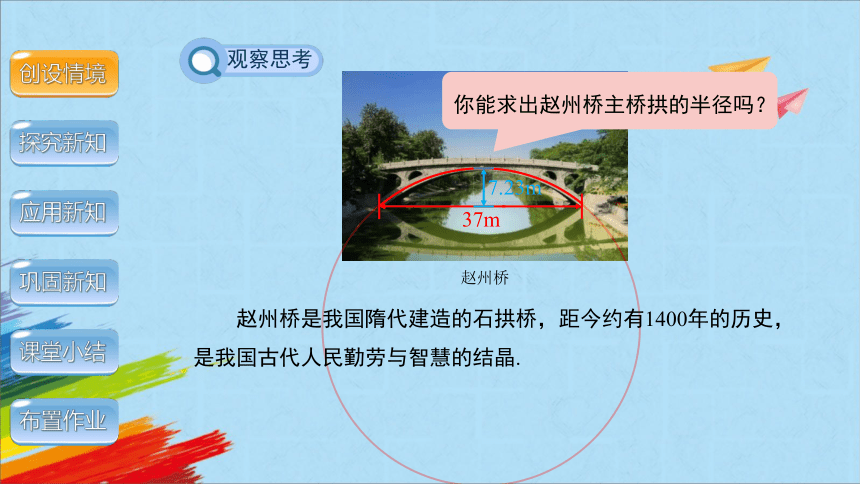
你能求出赵州桥主桥拱的半径吗?
观察思考
赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
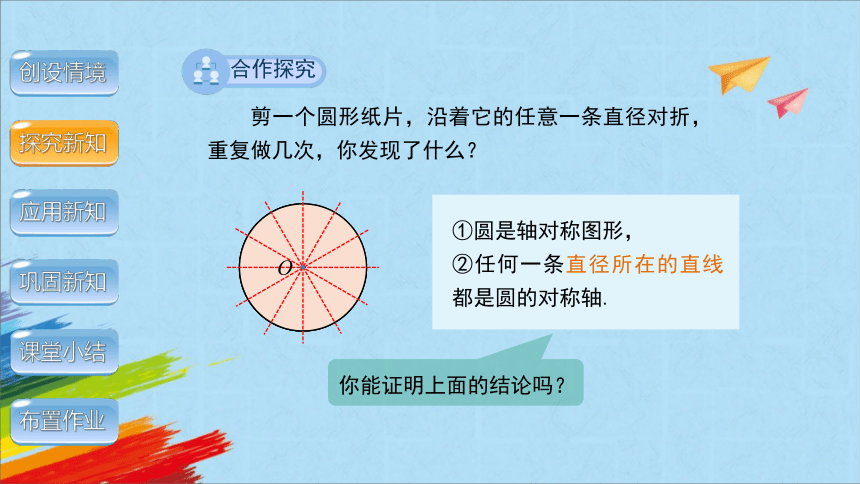
剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了什么?
O
①圆是轴对称图形,
②任何一条直径所在的直线都是圆的对称轴.
你能证明上面的结论吗?
合作探究
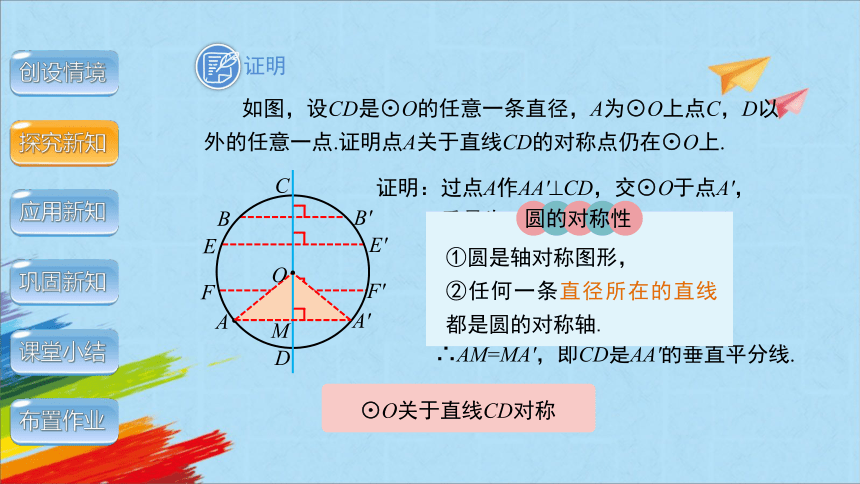
证明:过点A作AA' CD,交⊙O于点A',
垂足为M,连接OA,OA'
在△OAA'中,∵OA OA'
∴△OAA'是等腰三角形
又∵AA' CD
∴AM=MA',即CD是AA'的垂直平分线.
F
F'
E
E'
B
B'
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
证明
如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.证明点A关于直线CD的对称点仍在⊙O上.
C
D
A
A'
M
O
⊙O关于直线CD对称
圆的对称性
①圆是轴对称图形,
②任何一条直径所在的直线都是圆的对称轴.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
O
A
A'
M
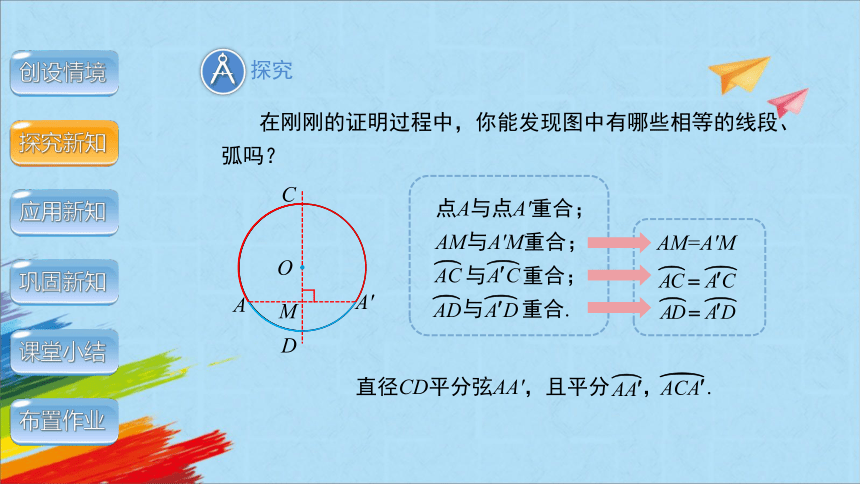
直径CD平分弦AA',且平分 , .
AM=A'M
C
D
点A与点A'重合;
AM与A'M重合;
与 重合;
与 重合.
在刚刚的证明过程中,你能发现图中有哪些相等的线段、弧吗?
题设:
①CD是⊙O直径
②CD AB
①直径
②垂直于弦
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
E
C
O
A
B
D
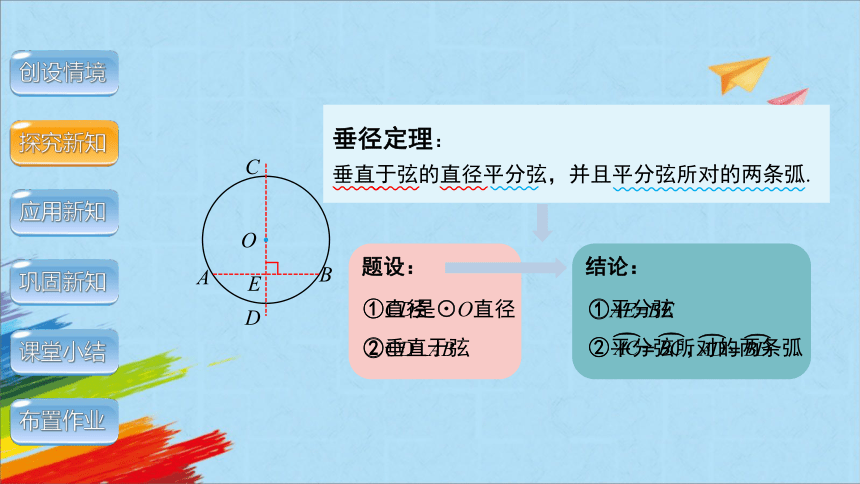
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
结论:
①平分弦
②平分弦所对的两条弧
①AE BE
② ,
想一想
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
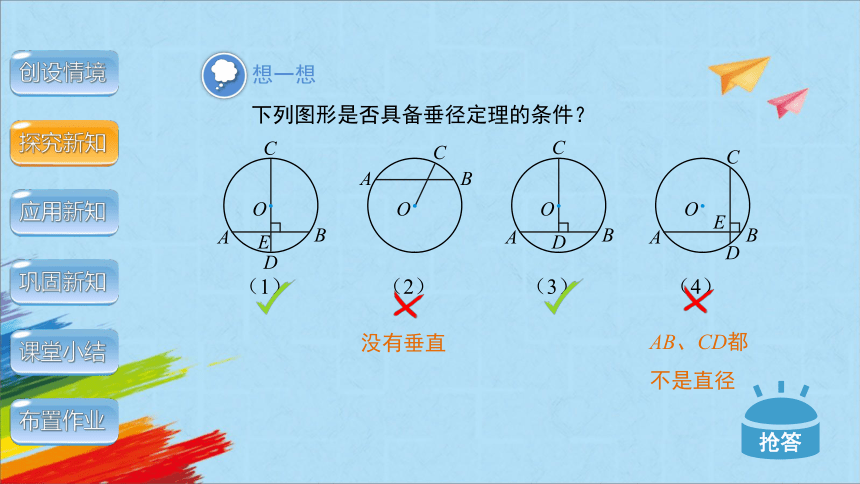
下列图形是否具备垂径定理的条件?
E
C
O
A
B
D
E
C
O
A
B
D
C
O
A
B
(1)
(2)
(3)
(4)
没有垂直
AB、CD都不是直径
D
O
A
B
C
抢答
想一想
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
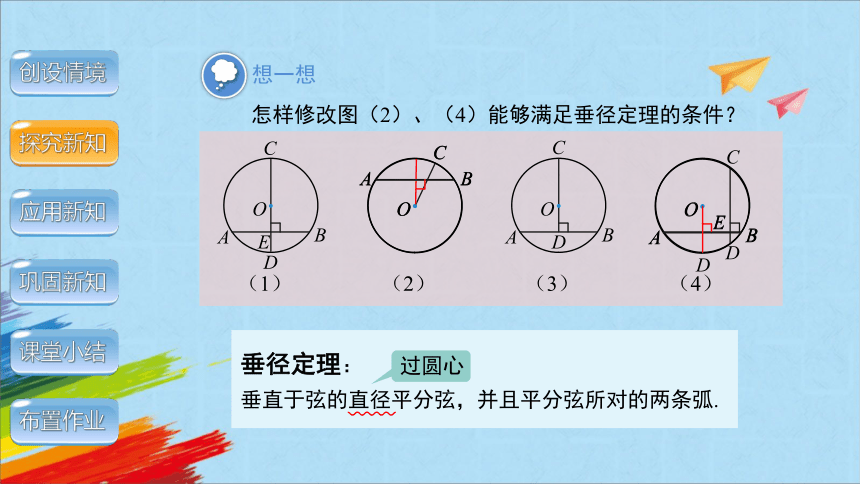
怎样修改图(2)、(4)能够满足垂径定理的条件?
E
C
O
A
B
D
E
C
O
A
B
D
C
O
A
B
(1)
(2)
(3)
(4)
D
O
A
B
C
C
O
A
B
E
O
A
B
D
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
过圆心
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
当直径CD平分一条弦AB(不是直径)时,能否得出CD AB
O
A
B
C
D
E
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
为什么?
圆的任意两条直径都互相平分,但它们不一定互相垂直.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
判断下列说法是否正确:
1.垂直于弦的直线平分弦,并且平分弦所对的两条弧.
2.平分弦的直径垂直于弦.
C
O
A
B
D
E
C
O
A
B
D
3.平分一条直径的弦必垂直于这条直径.
过圆心
不是直径
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
①过圆心,
②垂直于弦,
③平分弦,
④平分弦所对的优弧,
⑤平分弦所对的劣弧.
④平分弦所对的弧,
①②→③④⑤
①③→②④⑤
还有别的结论吗?
如:①④→②③⑤?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
①过圆心,②垂直于弦,③平分弦,
④平分弦所对的优弧,⑤平分弦所对的劣弧.
条件 结论
①②
③④⑤
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
①③
②④⑤
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
①④
②③⑤
①⑤
②③④
平分弦所对的一条弧的直径,垂直平分这条弦,并且平分弦所对的另一条弧.
②③
①⑤④
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
… …
… …
… …
知二推三
B
A
O
D
C
R
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1:赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱的半径(结果保留小数点后一位).
37m
7.23m
解:如图 表示主桥拱,设 所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,D为垂足,OC与 相交于点C,连接OA,
根据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
B
A
O
D
C
R
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1:赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱的半径(结果保留小数点后一位).
由题设可知:AB 37,CD 7.23,
∴AD AB 37 18.5,
OD OC CD R 7.23,
在Rt△OAD中,由勾股定理得:
OA2 AD2 OD2,即:R2 18.52 (R 7.23)2
解得:R 27.3.
因此,赵州桥的主桥拱半径约为27.3m.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
1. 在⊙O中,若CD AB于M,AB为直径,则下列结论不正确的是( )
A.
B.
C. AM OM
D. CM DM
M
A
O
C
D
B
C
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
2. 已知⊙O的直径AB 10,弦CD AB于M,OM 3,则CD .
M
A
O
C
D
B
8
5
3
4
3. 在⊙O中,弦CD AB于M,AB为直径,若CD 10, AM 1,则⊙O的半径为 .
M
B
O
C
D
A
r
1
5
r 1
(r 1)2 52 r2
13
解决有关弦的问题时,半径是常用的一种辅助线的添法.往往结合勾股定理计算.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
4.⊙O的半径为13cm,AB、CD是⊙O的两条弦,AB∥CD,AB=24cm,CD=10cm,求AB和CD之间的距离.
M
A
O
C
D
B
N
解:过点O向AB,CD作垂线,垂足分别为M,N,连接OB,OD.
由垂径定理可得:
BM AB 12cm,DN CD 5cm
又∵OB OD 13cm
在Rt△OBM, Rt△ODN中,
由勾股定理得:OM 5cm,ON 12cm
∴AB和CD之间的距离MN OM ON 7cm
或MN OM ON 17cm
M
N
O
A
C
D
B
分类讨论
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
垂径定理
简单计算
垂直于弦的直径
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
通常添加半径做辅助线,构造直角三角形,结合勾股定理进行计算或证明.
布置作业
教科书第83页
练习第1、2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
24.1.2 垂直于弦的直径
学习目标
1.探索圆的对称性,进而得到垂径定理及其推论;
2.能利用垂径定理及其推论解决相关证明、计算及实际问题;
3.经历探索垂径定理及其推论的过程,发展推理能力,让学生领会数学的严谨性,培养学生实事求是的科学态度;
4.进一步体会和理解研究几何图形的各种方法;培养学生独立探索,相互合作交流的精神,并体验发现的乐趣.
垂直于弦的直径
赵州桥
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
37m
7.23m
你能求出赵州桥主桥拱的半径吗?
观察思考
赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了什么?
O
①圆是轴对称图形,
②任何一条直径所在的直线都是圆的对称轴.
你能证明上面的结论吗?
合作探究
证明:过点A作AA' CD,交⊙O于点A',
垂足为M,连接OA,OA'
在△OAA'中,∵OA OA'
∴△OAA'是等腰三角形
又∵AA' CD
∴AM=MA',即CD是AA'的垂直平分线.
F
F'
E
E'
B
B'
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
证明
如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.证明点A关于直线CD的对称点仍在⊙O上.
C
D
A
A'
M
O
⊙O关于直线CD对称
圆的对称性
①圆是轴对称图形,
②任何一条直径所在的直线都是圆的对称轴.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
O
A
A'
M
直径CD平分弦AA',且平分 , .
AM=A'M
C
D
点A与点A'重合;
AM与A'M重合;
与 重合;
与 重合.
在刚刚的证明过程中,你能发现图中有哪些相等的线段、弧吗?
题设:
①CD是⊙O直径
②CD AB
①直径
②垂直于弦
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
E
C
O
A
B
D
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
结论:
①平分弦
②平分弦所对的两条弧
①AE BE
② ,
想一想
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
下列图形是否具备垂径定理的条件?
E
C
O
A
B
D
E
C
O
A
B
D
C
O
A
B
(1)
(2)
(3)
(4)
没有垂直
AB、CD都不是直径
D
O
A
B
C
抢答
想一想
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
怎样修改图(2)、(4)能够满足垂径定理的条件?
E
C
O
A
B
D
E
C
O
A
B
D
C
O
A
B
(1)
(2)
(3)
(4)
D
O
A
B
C
C
O
A
B
E
O
A
B
D
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
过圆心
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
当直径CD平分一条弦AB(不是直径)时,能否得出CD AB
O
A
B
C
D
E
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
为什么?
圆的任意两条直径都互相平分,但它们不一定互相垂直.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
判断下列说法是否正确:
1.垂直于弦的直线平分弦,并且平分弦所对的两条弧.
2.平分弦的直径垂直于弦.
C
O
A
B
D
E
C
O
A
B
D
3.平分一条直径的弦必垂直于这条直径.
过圆心
不是直径
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
①过圆心,
②垂直于弦,
③平分弦,
④平分弦所对的优弧,
⑤平分弦所对的劣弧.
④平分弦所对的弧,
①②→③④⑤
①③→②④⑤
还有别的结论吗?
如:①④→②③⑤?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
延伸
①过圆心,②垂直于弦,③平分弦,
④平分弦所对的优弧,⑤平分弦所对的劣弧.
条件 结论
①②
③④⑤
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
①③
②④⑤
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
①④
②③⑤
①⑤
②③④
平分弦所对的一条弧的直径,垂直平分这条弦,并且平分弦所对的另一条弧.
②③
①⑤④
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
… …
… …
… …
知二推三
B
A
O
D
C
R
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1:赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱的半径(结果保留小数点后一位).
37m
7.23m
解:如图 表示主桥拱,设 所在的圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC,D为垂足,OC与 相交于点C,连接OA,
根据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
B
A
O
D
C
R
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1:赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱的半径(结果保留小数点后一位).
由题设可知:AB 37,CD 7.23,
∴AD AB 37 18.5,
OD OC CD R 7.23,
在Rt△OAD中,由勾股定理得:
OA2 AD2 OD2,即:R2 18.52 (R 7.23)2
解得:R 27.3.
因此,赵州桥的主桥拱半径约为27.3m.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
1. 在⊙O中,若CD AB于M,AB为直径,则下列结论不正确的是( )
A.
B.
C. AM OM
D. CM DM
M
A
O
C
D
B
C
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
2. 已知⊙O的直径AB 10,弦CD AB于M,OM 3,则CD .
M
A
O
C
D
B
8
5
3
4
3. 在⊙O中,弦CD AB于M,AB为直径,若CD 10, AM 1,则⊙O的半径为 .
M
B
O
C
D
A
r
1
5
r 1
(r 1)2 52 r2
13
解决有关弦的问题时,半径是常用的一种辅助线的添法.往往结合勾股定理计算.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
4.⊙O的半径为13cm,AB、CD是⊙O的两条弦,AB∥CD,AB=24cm,CD=10cm,求AB和CD之间的距离.
M
A
O
C
D
B
N
解:过点O向AB,CD作垂线,垂足分别为M,N,连接OB,OD.
由垂径定理可得:
BM AB 12cm,DN CD 5cm
又∵OB OD 13cm
在Rt△OBM, Rt△ODN中,
由勾股定理得:OM 5cm,ON 12cm
∴AB和CD之间的距离MN OM ON 7cm
或MN OM ON 17cm
M
N
O
A
C
D
B
分类讨论
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
垂径定理
简单计算
垂直于弦的直径
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理的推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
通常添加半径做辅助线,构造直角三角形,结合勾股定理进行计算或证明.
布置作业
教科书第83页
练习第1、2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
