人教版九年级数学上册23.2.3关于原点对称的点的坐标 教学课件(共21张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.2.3关于原点对称的点的坐标 教学课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 13:57:15 | ||
图片预览





文档简介
(共21张PPT)
23.2.3关于原点对称的点的坐标
学习目标
1.能够正确认识关于原点对称的两点的坐标间的关系.
2.能够运用关于原点对称的两点的坐标间的关系,在平面直角坐标系中作图.
3.经历了观察、操作、交流、归纳等过程,培养学生探究问题的能力、动手能力、观察能力、以及与他人合作交流的能力.
4.通过学习平面直角坐标系内点的坐标对称的关系,培养学生善于归纳类比的学习精神.
关于原点对称的点的坐标
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
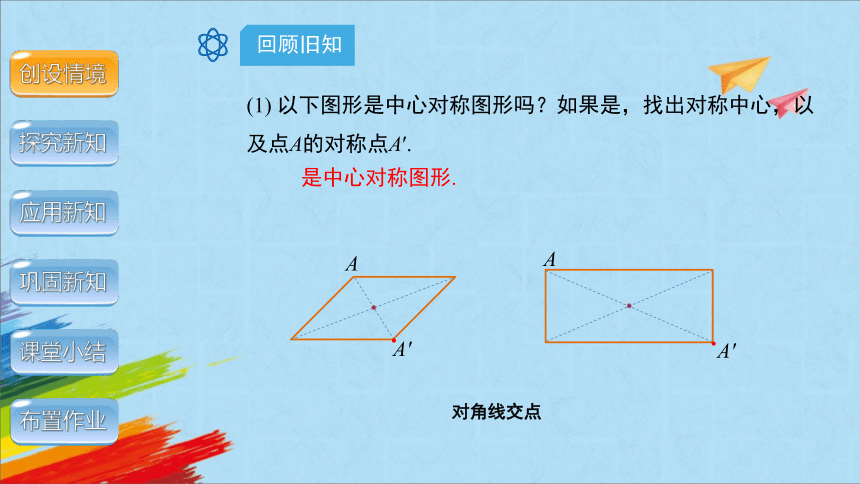
(1) 以下图形是中心对称图形吗?如果是,找出对称中心,以及点A的对称点A′.
对角线交点
是中心对称图形.
A
A′
A′
A
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
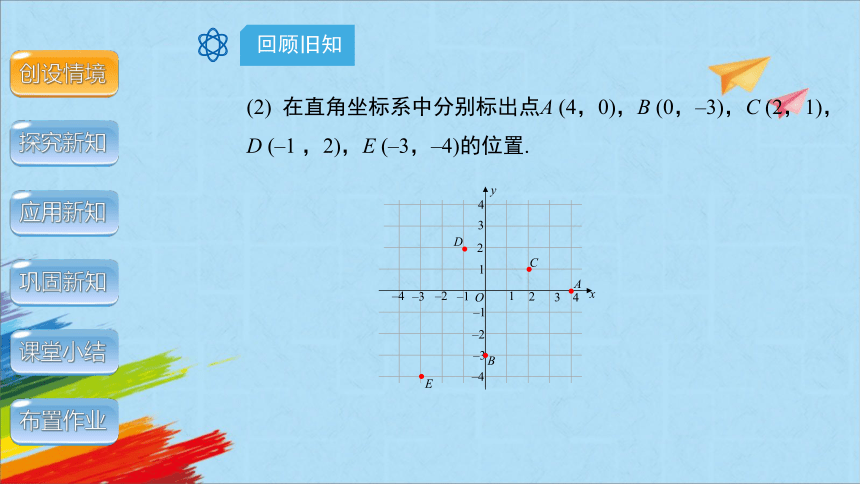
(2) 在直角坐标系中分别标出点A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4)的位置.
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
A
B
C
D
E
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
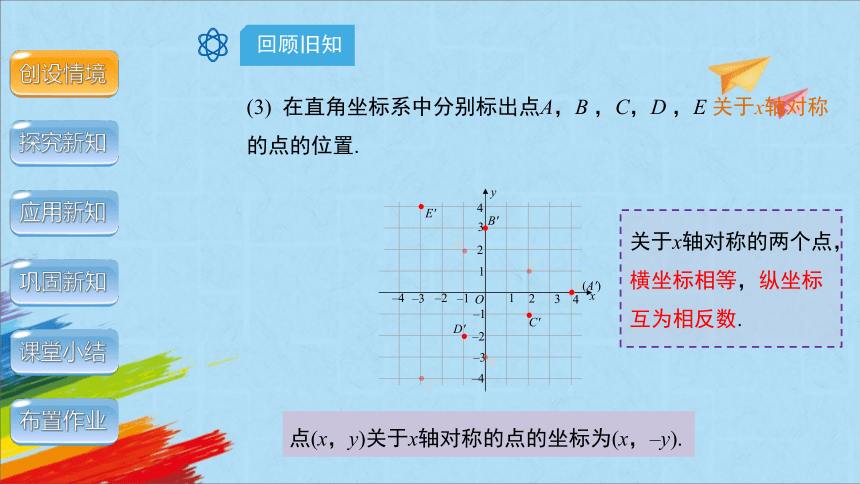
(3) 在直角坐标系中分别标出点A,B ,C,D ,E 关于x轴对称的点的位置.
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
A
B
C
D
E
D′
(A′)
B′
C′
E′
关于x轴对称的两个点,横坐标相等,纵坐标互为相反数.
点(x,y)关于x轴对称的点的坐标为(x,–y).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
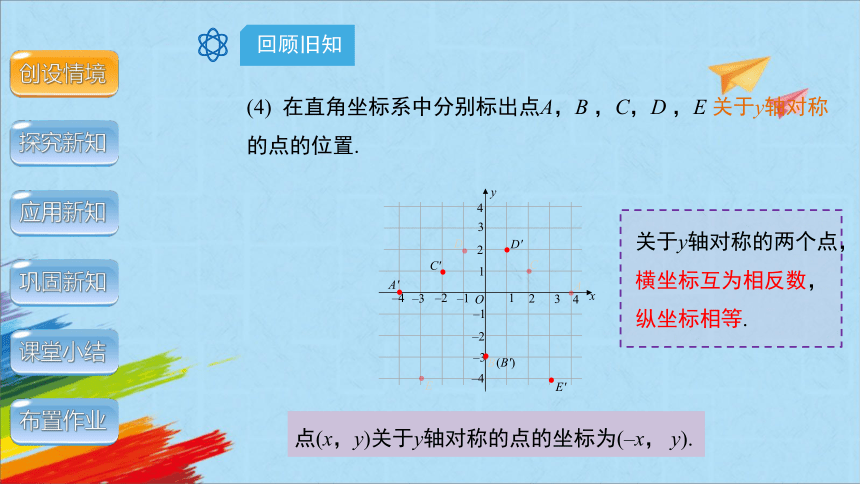
(4) 在直角坐标系中分别标出点A,B ,C,D ,E 关于y轴对称的点的位置.
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
A
B
C
D
E
D′
A′
(B′)
C′
E′
点(x,y)关于y轴对称的点的坐标为(–x, y).
关于y轴对称的两个点,横坐标互为相反数,纵坐标相等.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.
A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4).
探究
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
A
B
C
D
E
A′
A
O
D′
A′ (– 4,0),B ′ (0,3),C ′ (–2,–1),D ′(1 ,–2),E ′ (3,4).
(1,–2)
A′
(–4 ,0)
B′
(0 ,3)
C′
(–2 ,–1)
E′
(3,4)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题1:在直角坐标系中,关于原点对称的两个点,它们的横坐标什么关系?
探究
E ′ (3,4)
E (–3,–4)
A (4,0)
B (0,–3)
C (2,1)
D (–1 ,2)
A′ (– 4,0)
B ′ (0,3)
C ′ (–2,–1)
D ′(1 ,–2)
关于原点O的对称点
横坐标互为相反数
→
→
→
→
→
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题2:在直角坐标系中,关于原点对称的两个点,它们的纵坐标什么关系?
探究
E ′ (3,4)
E (–3,–4)
A (4,0)
B (0,–3)
C (2,1)
D (–1 ,2)
A′ (– 4,0)
B ′ (0,3)
C ′ (–2,–1)
D ′(1 ,–2)
纵坐标互为相反数
→
→
→
→
→
关于原点O的对称点
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
P(x,y)
P′ (–x,–y)
关于原点O的对称点
P(x,y)
P′ (x,–y)
关于x轴的对称点
P(x,y)
P′ (–x,y)
关于y轴的对称点
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
1. 写出下列各点关于原点的对称点的坐标:
(1)点A(3,1)关于原点对称的点的坐标A′( , );
(2)点B( – 2 ,3)关于原点对称的点的坐标B′( , );
(3)点C( – 1, – 2)关于原点对称的点的坐标C′( , );
(4)点D( 2, – 3)关于原点对称的点的坐标C′( , ).
–3
–1
2
–3
1
2
–2
3
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
2. 下列各点中哪两个点关于原点对称?
A(–5,0)、B(0,2)、C(2,–1)、D(2,0)、E(0,5)、 F(–2,1)、G (–2,–1).
解:C(2,–1)与 F(–2,1)关于原点对称.
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图所示,利用关于原点对称的点的坐标的关系,作出与△ABC 关于原点对称的图形.
解:点P(x,y) 关于原点的对称点为P′(–x,–y),
△ABC 的三个顶点A(–4,1),B(–1,–1),C(–3,2),
关于原点的对称点分别为
A′(4,–1),
B′(1,1),
C′(3,–2),
依次连接A′B′,B′C′,C′A′,就可得到与△ABC 关于原点对称的△A′B′C′.
A′
B′
C′
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
归纳
在直角坐标系中,画一个图形关于原点对称的图形的一般步骤:
1. 确定关键点(通常为图形顶点等特殊点)的坐标.
2. 求出关键点关于原点的对称点的坐标,并在直角坐标系中标出.
3. 顺次连接对称点,组成的图形为所求.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
填空:
若设点M(a,b),
点M关于x轴的对称点M1 ( , );
点M关于y轴的对称点M2 ( , );
点M关于O轴的对称点M3 ( , ).
a
–b
– a
b
– a
–b
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
填空:
已知点A(–1, – 3),
关于x轴对称的点的坐标是_________;
关于y轴对称的点的坐标是_________;
关于原点对称的点的坐标是________.
(–1,3)
(1, –3)
(1,3)
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
填空:
点A(m, – 2), B(1, n)关于x轴对称,则m=____,n=____.
点A(m, – 2), B(1, n)关于y轴对称,则m=_____,n=_____.
点A(m, – 2), B(1, n)关于原点对称,则m=_____,n=_____.
1
2
–1
–2
–1
2
应用新知
课堂小结
布置作业
创设情境
练习4
随堂练习
探究新知
巩固新知
在如图所示编号为①、②、③、④的四个三角形中,关于x轴对称的两个三角形的编号为_________;关于y轴对称的两个三角形的编号为_________;关于原点O对称的两个三角形的编号为__________.
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
①
②
③
④
①与③
①与②
②与③
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
关于原点对称的点的坐标
P(x, y)
P′ (–x, –y)
关于x轴的对称点
P(x, y)
P′ (–x, –y)
关于y轴的对称点
P(x, y)
P′ (–x, –y)
关于原点O的对称点
在直角坐标系中,画一个图形关于原点对称的图形的一般步骤:
1. 确定关键点(通常为图形顶点等特殊点)的坐标.
2. 求出关键点关于原点的对称点的坐标,并在直角坐标系中标出.
3. 顺次连接对称点,组成的图形为所求.
布置作业
教科书第69页,练习3.
第70页,习题3、4.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
23.2.3关于原点对称的点的坐标
学习目标
1.能够正确认识关于原点对称的两点的坐标间的关系.
2.能够运用关于原点对称的两点的坐标间的关系,在平面直角坐标系中作图.
3.经历了观察、操作、交流、归纳等过程,培养学生探究问题的能力、动手能力、观察能力、以及与他人合作交流的能力.
4.通过学习平面直角坐标系内点的坐标对称的关系,培养学生善于归纳类比的学习精神.
关于原点对称的点的坐标
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
(1) 以下图形是中心对称图形吗?如果是,找出对称中心,以及点A的对称点A′.
对角线交点
是中心对称图形.
A
A′
A′
A
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
(2) 在直角坐标系中分别标出点A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4)的位置.
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
A
B
C
D
E
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
(3) 在直角坐标系中分别标出点A,B ,C,D ,E 关于x轴对称的点的位置.
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
A
B
C
D
E
D′
(A′)
B′
C′
E′
关于x轴对称的两个点,横坐标相等,纵坐标互为相反数.
点(x,y)关于x轴对称的点的坐标为(x,–y).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
(4) 在直角坐标系中分别标出点A,B ,C,D ,E 关于y轴对称的点的位置.
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
A
B
C
D
E
D′
A′
(B′)
C′
E′
点(x,y)关于y轴对称的点的坐标为(–x, y).
关于y轴对称的两个点,横坐标互为相反数,纵坐标相等.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.
A (4,0),B (0,–3),C (2,1),D (–1 ,2),E (–3,–4).
探究
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
A
B
C
D
E
A′
A
O
D′
A′ (– 4,0),B ′ (0,3),C ′ (–2,–1),D ′(1 ,–2),E ′ (3,4).
(1,–2)
A′
(–4 ,0)
B′
(0 ,3)
C′
(–2 ,–1)
E′
(3,4)
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题1:在直角坐标系中,关于原点对称的两个点,它们的横坐标什么关系?
探究
E ′ (3,4)
E (–3,–4)
A (4,0)
B (0,–3)
C (2,1)
D (–1 ,2)
A′ (– 4,0)
B ′ (0,3)
C ′ (–2,–1)
D ′(1 ,–2)
关于原点O的对称点
横坐标互为相反数
→
→
→
→
→
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题2:在直角坐标系中,关于原点对称的两个点,它们的纵坐标什么关系?
探究
E ′ (3,4)
E (–3,–4)
A (4,0)
B (0,–3)
C (2,1)
D (–1 ,2)
A′ (– 4,0)
B ′ (0,3)
C ′ (–2,–1)
D ′(1 ,–2)
纵坐标互为相反数
→
→
→
→
→
关于原点O的对称点
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
P(x,y)
P′ (–x,–y)
关于原点O的对称点
P(x,y)
P′ (x,–y)
关于x轴的对称点
P(x,y)
P′ (–x,y)
关于y轴的对称点
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
1. 写出下列各点关于原点的对称点的坐标:
(1)点A(3,1)关于原点对称的点的坐标A′( , );
(2)点B( – 2 ,3)关于原点对称的点的坐标B′( , );
(3)点C( – 1, – 2)关于原点对称的点的坐标C′( , );
(4)点D( 2, – 3)关于原点对称的点的坐标C′( , ).
–3
–1
2
–3
1
2
–2
3
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
2. 下列各点中哪两个点关于原点对称?
A(–5,0)、B(0,2)、C(2,–1)、D(2,0)、E(0,5)、 F(–2,1)、G (–2,–1).
解:C(2,–1)与 F(–2,1)关于原点对称.
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图所示,利用关于原点对称的点的坐标的关系,作出与△ABC 关于原点对称的图形.
解:点P(x,y) 关于原点的对称点为P′(–x,–y),
△ABC 的三个顶点A(–4,1),B(–1,–1),C(–3,2),
关于原点的对称点分别为
A′(4,–1),
B′(1,1),
C′(3,–2),
依次连接A′B′,B′C′,C′A′,就可得到与△ABC 关于原点对称的△A′B′C′.
A′
B′
C′
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
归纳
在直角坐标系中,画一个图形关于原点对称的图形的一般步骤:
1. 确定关键点(通常为图形顶点等特殊点)的坐标.
2. 求出关键点关于原点的对称点的坐标,并在直角坐标系中标出.
3. 顺次连接对称点,组成的图形为所求.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
填空:
若设点M(a,b),
点M关于x轴的对称点M1 ( , );
点M关于y轴的对称点M2 ( , );
点M关于O轴的对称点M3 ( , ).
a
–b
– a
b
– a
–b
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
填空:
已知点A(–1, – 3),
关于x轴对称的点的坐标是_________;
关于y轴对称的点的坐标是_________;
关于原点对称的点的坐标是________.
(–1,3)
(1, –3)
(1,3)
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
填空:
点A(m, – 2), B(1, n)关于x轴对称,则m=____,n=____.
点A(m, – 2), B(1, n)关于y轴对称,则m=_____,n=_____.
点A(m, – 2), B(1, n)关于原点对称,则m=_____,n=_____.
1
2
–1
–2
–1
2
应用新知
课堂小结
布置作业
创设情境
练习4
随堂练习
探究新知
巩固新知
在如图所示编号为①、②、③、④的四个三角形中,关于x轴对称的两个三角形的编号为_________;关于y轴对称的两个三角形的编号为_________;关于原点O对称的两个三角形的编号为__________.
O
x
y
1
2
3
–1
–2
–3
–4
1
2
3
–1
–2
–3
–4
4
4
①
②
③
④
①与③
①与②
②与③
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
关于原点对称的点的坐标
P(x, y)
P′ (–x, –y)
关于x轴的对称点
P(x, y)
P′ (–x, –y)
关于y轴的对称点
P(x, y)
P′ (–x, –y)
关于原点O的对称点
在直角坐标系中,画一个图形关于原点对称的图形的一般步骤:
1. 确定关键点(通常为图形顶点等特殊点)的坐标.
2. 求出关键点关于原点的对称点的坐标,并在直角坐标系中标出.
3. 顺次连接对称点,组成的图形为所求.
布置作业
教科书第69页,练习3.
第70页,习题3、4.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
