人教版九年级数学上册22.3《实际问题与二次函数》第1课时 教学课件(共14张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.3《实际问题与二次函数》第1课时 教学课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 15:02:43 | ||
图片预览



文档简介
(共14张PPT)
22.3实际问题与二次函数
第1课时
学习目标
1.能根据具体几何问题中的数量关系,列出二次函数解析式,并能应用二次函数的相关性质解决面积问题;
2.经历运用二次函数的性质解决实际问题的过程,体会“数形结合”的思想;
3.通过建立实际问题与二次函数的联系,提高学生数学建模的能力;
4.通过用二次函数解决实际生活中的问题,体会函数知识的应用价值,感受数学与人类生活的密切联系.
面
积问题
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
二次函数
还记得如何求二次函数的最值吗?
一起去回顾一下吧!
最大高度
最大高度
二次函数的
最值
观察与思考
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
回顾与思考
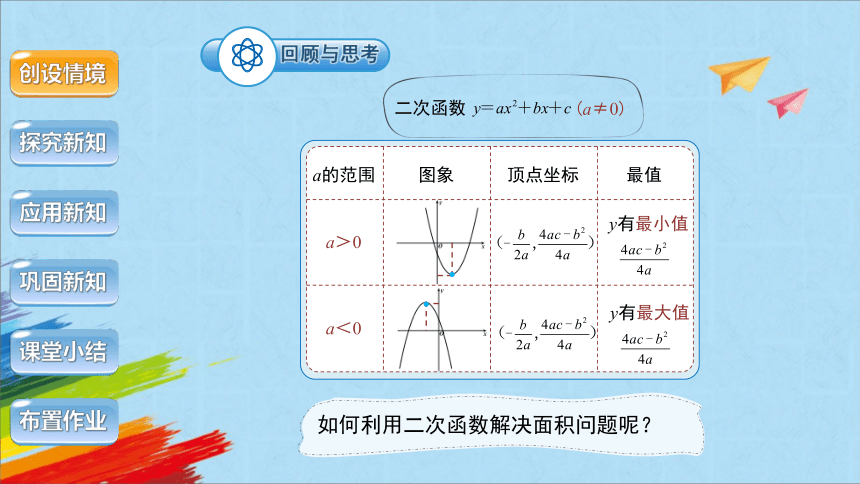
二次函数
a的范围
图象
最值
顶点坐标
a>0
a<0
( , )
y有最小值
( , )
y有最大值
(a≠0)
如何利用二次函数解决面积问题呢?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
你能画一个周长为60 cm的矩形吗?
这些矩形的面积一定相等吗?
不一定
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
当周长为60 cm时,你能画出一个面积最大的矩形吗?
分组交流讨论:
1.学生分组交流讨论;
2.各组展示方法过程;
3.教师带领大家完善探究过程.
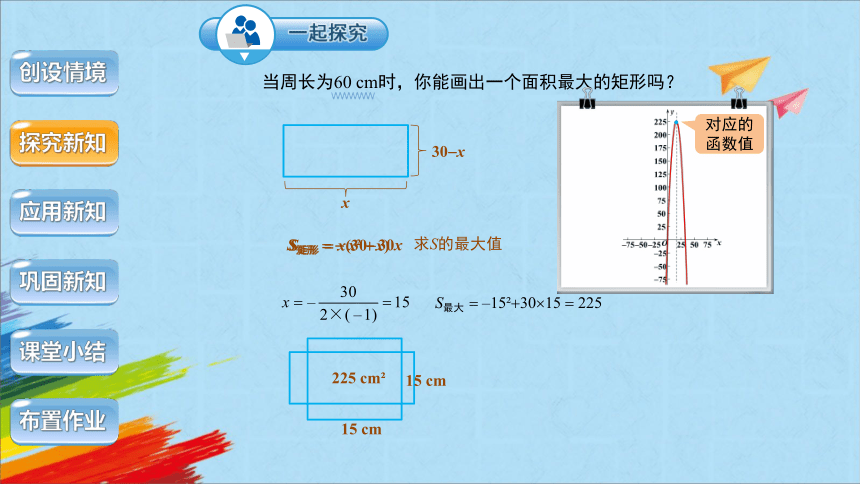
当周长为60 cm时,你能画出一个面积最大的矩形吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
x
30 x
S矩形 x(30 x)
S矩形 x 30x
S最大 –15 30 15 225
15 cm
15 cm
225 cm
求S的最大值
对应的函数值
例:如图,用一段长为60 m的篱笆围成一个一边靠墙的矩形菜园,墙长32 m,这个矩形与墙平行的一边长为x m,则当x为多少时,菜园的面积最大,最大面积是多少?
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
32m
(1)菜园另一边的长= m,菜园的面积= .
(2) x的取值范围是 .
(3) 当x= 时,菜园面积最大,最大面积= .
思考:
x
0<x≤32
30
450 m
创设情境
例:如图,用一段长为60 m的篱笆围成一个一边靠墙的矩形菜园,墙长32 m,这个矩形与墙平行的一边长为x m,则当x为多少时,菜园的面积最大,最大面积是多少?
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
32m
x
解:菜园的一边长为x m,则另一边的长为 m,所以菜园的面积为
当 时,菜园的面积最大,
所以菜园的最大面积为450 m .
(0<x≤32)
创设情境
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.已知一个直角三角形两直角边之和为20 cm,则这个直角
三角形的最大面积为( )
A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
B
2.在综合实践活动中,同学们借助如图所示的直角墙角(两边足够长),用24 m长的篱笆围成一个矩形花园ABCD,则矩形花园ABCD的最大面积为 .
144 m2
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.若把一根长为120 cm的铁丝分成两部分 ,每一部分均弯曲
成一个正方形,它们的面积和最小是多少?
解:设将铁丝分成长为x cm,(120-x )cm的两段,并分别围成正方形,则正方形的边长分别为 cm, cm.
设它们的面积和为y cm2,则
当x=60时,y的最小值为450.
所以,它们的面积和最小为450 cm2.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
实际问题与二次函数
—最大面积问题
实际问题
二次函数的最值
实际问题与二次函数的联系
二次函数
建立模型
二次函数的最值
(a≠0)
布置作业
教科书第51-52页
习题22.3
第1、4、5题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再 见
22.3实际问题与二次函数
第1课时
学习目标
1.能根据具体几何问题中的数量关系,列出二次函数解析式,并能应用二次函数的相关性质解决面积问题;
2.经历运用二次函数的性质解决实际问题的过程,体会“数形结合”的思想;
3.通过建立实际问题与二次函数的联系,提高学生数学建模的能力;
4.通过用二次函数解决实际生活中的问题,体会函数知识的应用价值,感受数学与人类生活的密切联系.
面
积问题
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
二次函数
还记得如何求二次函数的最值吗?
一起去回顾一下吧!
最大高度
最大高度
二次函数的
最值
观察与思考
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
回顾与思考
二次函数
a的范围
图象
最值
顶点坐标
a>0
a<0
( , )
y有最小值
( , )
y有最大值
(a≠0)
如何利用二次函数解决面积问题呢?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
你能画一个周长为60 cm的矩形吗?
这些矩形的面积一定相等吗?
不一定
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
当周长为60 cm时,你能画出一个面积最大的矩形吗?
分组交流讨论:
1.学生分组交流讨论;
2.各组展示方法过程;
3.教师带领大家完善探究过程.
当周长为60 cm时,你能画出一个面积最大的矩形吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
一起探究
x
30 x
S矩形 x(30 x)
S矩形 x 30x
S最大 –15 30 15 225
15 cm
15 cm
225 cm
求S的最大值
对应的函数值
例:如图,用一段长为60 m的篱笆围成一个一边靠墙的矩形菜园,墙长32 m,这个矩形与墙平行的一边长为x m,则当x为多少时,菜园的面积最大,最大面积是多少?
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
32m
(1)菜园另一边的长= m,菜园的面积= .
(2) x的取值范围是 .
(3) 当x= 时,菜园面积最大,最大面积= .
思考:
x
0<x≤32
30
450 m
创设情境
例:如图,用一段长为60 m的篱笆围成一个一边靠墙的矩形菜园,墙长32 m,这个矩形与墙平行的一边长为x m,则当x为多少时,菜园的面积最大,最大面积是多少?
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
32m
x
解:菜园的一边长为x m,则另一边的长为 m,所以菜园的面积为
当 时,菜园的面积最大,
所以菜园的最大面积为450 m .
(0<x≤32)
创设情境
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.已知一个直角三角形两直角边之和为20 cm,则这个直角
三角形的最大面积为( )
A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
B
2.在综合实践活动中,同学们借助如图所示的直角墙角(两边足够长),用24 m长的篱笆围成一个矩形花园ABCD,则矩形花园ABCD的最大面积为 .
144 m2
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.若把一根长为120 cm的铁丝分成两部分 ,每一部分均弯曲
成一个正方形,它们的面积和最小是多少?
解:设将铁丝分成长为x cm,(120-x )cm的两段,并分别围成正方形,则正方形的边长分别为 cm, cm.
设它们的面积和为y cm2,则
当x=60时,y的最小值为450.
所以,它们的面积和最小为450 cm2.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
实际问题与二次函数
—最大面积问题
实际问题
二次函数的最值
实际问题与二次函数的联系
二次函数
建立模型
二次函数的最值
(a≠0)
布置作业
教科书第51-52页
习题22.3
第1、4、5题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再 见
同课章节目录
