人教版九年级数学上册25.2用列举法求概率 第1课时教学课件(共25张PPT)
文档属性
| 名称 | 人教版九年级数学上册25.2用列举法求概率 第1课时教学课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 15:06:38 | ||
图片预览







文档简介
(共25张PPT)
25.2 用列举法求概率
第1课时
学习目标
1.会用直接列举法和列表法求简单事件的概率;
2.能利用概率知识解决涉及两个因素的事件的概率问题;
3.经历试验、列表、统计、运算等活动,渗透数形结合,分类讨论、特殊到一般的思想,培养学生在具体情境中分析问题和解决问题的能力;
4.通过数学活动,体会数学的应用价值,培养积极思考的学习习惯.
用直接列举法和列表法求概率
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都______,事件A包含其中的m种结果,那么事件A发生的概率P(A) =______;事件A的概率P(A)的取值范围是:_____________.
相等
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
掷一枚硬币,正面向上的概率是______.
掷一枚硬币,可能出现的结果有2种:
正面朝上,反面朝上.
这两个结果出现的可能性是相同的.
列举出来
探究
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫列举法.
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
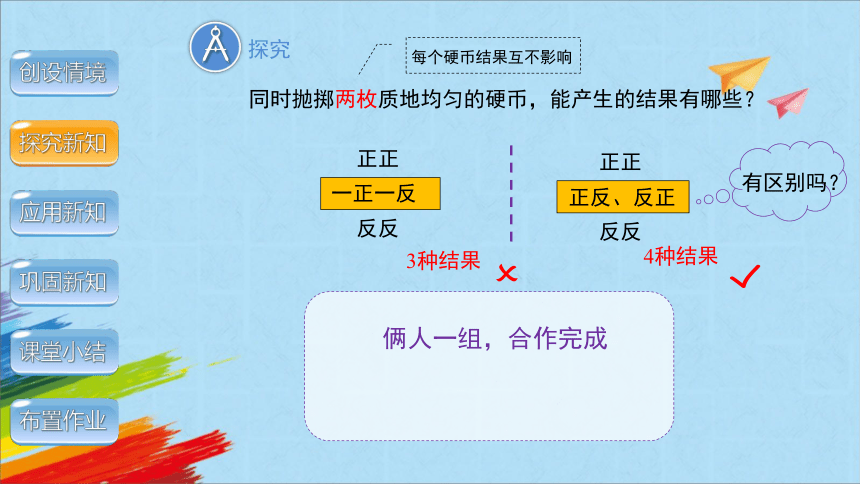
同时抛掷两枚质地均匀的硬币,能产生的结果有哪些?
俩人一组,合作完成
每个硬币结果互不影响
3种结果
4种结果
正正
一正一反
反反
正正
正反、反正
反反
有区别吗?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
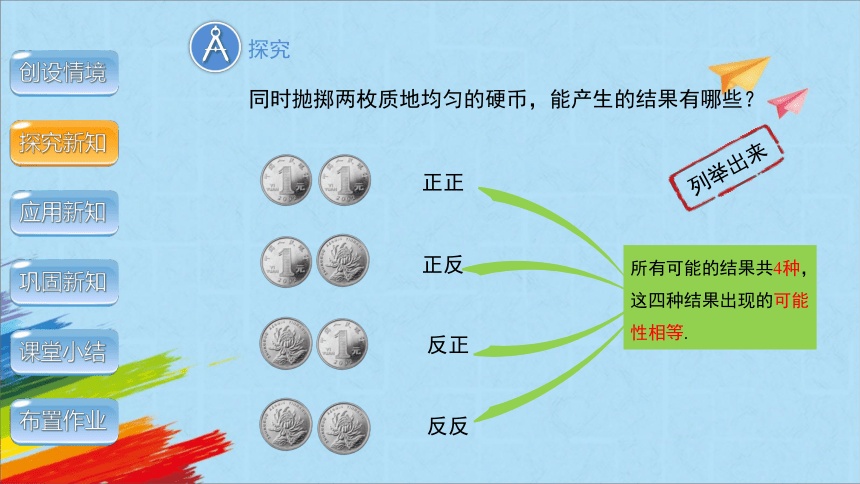
同时抛掷两枚质地均匀的硬币,能产生的结果有哪些?
正正
正反
反正
反反
所有可能的结果共4种,
这四种结果出现的可能性相等.
列举出来
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上;一枚硬币反面向上.
列举法
解:列举投掷两枚硬币所能产生的全部结果,它们是: .
所有可能的结果有 个,并且这些结果出现的 相等.
①满足两枚硬币全部正面向上(记为事件A) 的结果只有1种,即“正正”,所以P(A)= .
正正、正反、反正、反反
4
可能性
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上;一枚硬币反面向上.
列举法
解:列举投掷两枚硬币所能产生的全部结果,它们是: .
所有可能的结果有 个,并且这些结果出现的 相等.
②满足两枚硬币全部反面向上(记为事件B) 的结果只有1种,即“反反”, 所以P(B)= .
正正、正反、反正、反反
4
可能性
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面朝上;一枚硬币反面朝上.
列举法
解:列举投掷两枚硬币所能产生的全部结果,它们是: ,
所有可能的结果有 个,并且这些结果出现的 相等.
③满足一枚硬币正面向上;一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反” ,所以P(C)= .
正正、正反、反正、反反
4
可能性
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
先后两次抛掷一枚质地均匀的硬币,能产生的结果有哪些?
与同时抛掷两枚质地均匀的硬币产生的结果一样吗?
俩人一组,合作完成
正正
正反
反正
反反
所有可能的结果共4种,
这四种结果出现的可能性相等.
先抛掷的
后抛掷的
一样
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是 9;
(3)至少有一枚骰子的点数为 2.
当一次试验是掷两枚骰子时,为不重不漏地列出所有可能的结果,通常采用列表法.
两个因素
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
解:两枚骰子分别记为第 1 枚和第 2 枚,可以用下表列举出所有可能的结果.用(第1枚点数,第2枚点数)的形式表示结果.
第1枚
第2枚
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
列表法,分步进行
1 2 3 4 5 6
1 (3,1) (4,1) (5,1) (6,1)
2 (3,2) (4,2) (5,2) (6,2)
3 (3,3) (4,3) (5,3) (6,3)
4 (3,4) (4,4) (5,4) (6,4)
5 (3,5) (4,5) (5,5) (6,5)
6 (3,6) (4,6) (5,6) (6,6)
第1枚
第2枚
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
解:两枚骰子分别记为第 1 枚和第 2 枚,可以用下表列举出所有可能的结果.用(第1枚点数,第2枚点数)的形式表示结果.
可以看出,同时掷两枚骰子,可能出现的结果有36种,并且它们出现的可能性相等.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
两枚骰子点数相同(记为事件 A)的结果有 6种,即(1,1),
(2,2),(3,3),(4,4),(5,5),(6,6).
所以
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(2)两枚骰子点数的和是 9;
两枚骰子点数的和是 9 (记为事件 B)的结果有 4种,即
(3,6),(4,5),(5,4),(6,3).
所以
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(3)至少有一枚骰子的点数为2.
至少有一枚骰子的点数为2 (记为事件 C)的结果有 11种,即
(1,2),(2,2),(3,2),(4,2),(5,2),(6,2), (2,1),
(2,3),(2,4), ( 2,5),(2,6).
所以
归纳
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
1.用列举法(列表法)求简单随机事件的概率.
3.适用条件:
如果事件中各种结果出现的可能性相等,含有两次操作(如掷骰子两次)或两个条件(如掷两个骰子)的事件.
2.用列表法求概率的步骤:
①列表;
②通过表格计数,确定所有等可能的结果数n和关注的结果数m的值;
③利用概率公式 计算出事件的概率.
思考
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是 9;
(3)至少有一枚骰子的点数为 2.
俩人一组,合作完成
(1)两次骰子的点数相同;
(2)两次骰子点数的和是 9;
(3)至少有一次骰子的点数为 2.
把一枚掷质均匀的骰子投两次,
结果有变化吗?
没有变化
第1次
第2次
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
从1,2, 3三个数中,随机抽取两个数相乘,积是正数的概率是______.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为( )
A. B. C. D.
B
请用列表法写出所有可能的结果.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
随堂练习
小强
小华
剪刀
石头
布
剪刀
石头
布
(剪刀,剪刀)
(剪刀,石头)
(剪刀,布)
(石头,剪刀)
(石头,石头)
(石头,布)
(布,剪刀)
(布,石头)
(布,布)
小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
用直接列举法和列表法求概率
1.用列举法(列表法)求简单随机事件的概率.
3.适用条件:
如果事件中各种结果出现的可能性均等,含有两次操作(如掷骰子两次)或两个条件(如掷两个骰子)的事件.
2.用列表法求概率的步骤:
①列表;②通过表格计数,确定所有等可能的结果数n和关注的结果数m的值;③利用概率公式 计算出事件的概率.
布置作业
教科书第138页练习1、2.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
25.2 用列举法求概率
第1课时
学习目标
1.会用直接列举法和列表法求简单事件的概率;
2.能利用概率知识解决涉及两个因素的事件的概率问题;
3.经历试验、列表、统计、运算等活动,渗透数形结合,分类讨论、特殊到一般的思想,培养学生在具体情境中分析问题和解决问题的能力;
4.通过数学活动,体会数学的应用价值,培养积极思考的学习习惯.
用直接列举法和列表法求概率
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都______,事件A包含其中的m种结果,那么事件A发生的概率P(A) =______;事件A的概率P(A)的取值范围是:_____________.
相等
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
掷一枚硬币,正面向上的概率是______.
掷一枚硬币,可能出现的结果有2种:
正面朝上,反面朝上.
这两个结果出现的可能性是相同的.
列举出来
探究
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
在一次试验中,如果可能出现的结果只有有限个,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫列举法.
归纳
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
同时抛掷两枚质地均匀的硬币,能产生的结果有哪些?
俩人一组,合作完成
每个硬币结果互不影响
3种结果
4种结果
正正
一正一反
反反
正正
正反、反正
反反
有区别吗?
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
同时抛掷两枚质地均匀的硬币,能产生的结果有哪些?
正正
正反
反正
反反
所有可能的结果共4种,
这四种结果出现的可能性相等.
列举出来
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上;一枚硬币反面向上.
列举法
解:列举投掷两枚硬币所能产生的全部结果,它们是: .
所有可能的结果有 个,并且这些结果出现的 相等.
①满足两枚硬币全部正面向上(记为事件A) 的结果只有1种,即“正正”,所以P(A)= .
正正、正反、反正、反反
4
可能性
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上;一枚硬币反面向上.
列举法
解:列举投掷两枚硬币所能产生的全部结果,它们是: .
所有可能的结果有 个,并且这些结果出现的 相等.
②满足两枚硬币全部反面向上(记为事件B) 的结果只有1种,即“反反”, 所以P(B)= .
正正、正反、反正、反反
4
可能性
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
同时抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部正面向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面朝上;一枚硬币反面朝上.
列举法
解:列举投掷两枚硬币所能产生的全部结果,它们是: ,
所有可能的结果有 个,并且这些结果出现的 相等.
③满足一枚硬币正面向上;一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反” ,所以P(C)= .
正正、正反、反正、反反
4
可能性
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
探究
先后两次抛掷一枚质地均匀的硬币,能产生的结果有哪些?
与同时抛掷两枚质地均匀的硬币产生的结果一样吗?
俩人一组,合作完成
正正
正反
反正
反反
所有可能的结果共4种,
这四种结果出现的可能性相等.
先抛掷的
后抛掷的
一样
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是 9;
(3)至少有一枚骰子的点数为 2.
当一次试验是掷两枚骰子时,为不重不漏地列出所有可能的结果,通常采用列表法.
两个因素
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
解:两枚骰子分别记为第 1 枚和第 2 枚,可以用下表列举出所有可能的结果.用(第1枚点数,第2枚点数)的形式表示结果.
第1枚
第2枚
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
列表法,分步进行
1 2 3 4 5 6
1 (3,1) (4,1) (5,1) (6,1)
2 (3,2) (4,2) (5,2) (6,2)
3 (3,3) (4,3) (5,3) (6,3)
4 (3,4) (4,4) (5,4) (6,4)
5 (3,5) (4,5) (5,5) (6,5)
6 (3,6) (4,6) (5,6) (6,6)
第1枚
第2枚
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
解:两枚骰子分别记为第 1 枚和第 2 枚,可以用下表列举出所有可能的结果.用(第1枚点数,第2枚点数)的形式表示结果.
可以看出,同时掷两枚骰子,可能出现的结果有36种,并且它们出现的可能性相等.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
两枚骰子点数相同(记为事件 A)的结果有 6种,即(1,1),
(2,2),(3,3),(4,4),(5,5),(6,6).
所以
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(2)两枚骰子点数的和是 9;
两枚骰子点数的和是 9 (记为事件 B)的结果有 4种,即
(3,6),(4,5),(5,4),(6,3).
所以
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(3)至少有一枚骰子的点数为2.
至少有一枚骰子的点数为2 (记为事件 C)的结果有 11种,即
(1,2),(2,2),(3,2),(4,2),(5,2),(6,2), (2,1),
(2,3),(2,4), ( 2,5),(2,6).
所以
归纳
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
1.用列举法(列表法)求简单随机事件的概率.
3.适用条件:
如果事件中各种结果出现的可能性相等,含有两次操作(如掷骰子两次)或两个条件(如掷两个骰子)的事件.
2.用列表法求概率的步骤:
①列表;
②通过表格计数,确定所有等可能的结果数n和关注的结果数m的值;
③利用概率公式 计算出事件的概率.
思考
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子点数的和是 9;
(3)至少有一枚骰子的点数为 2.
俩人一组,合作完成
(1)两次骰子的点数相同;
(2)两次骰子点数的和是 9;
(3)至少有一次骰子的点数为 2.
把一枚掷质均匀的骰子投两次,
结果有变化吗?
没有变化
第1次
第2次
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
从1,2, 3三个数中,随机抽取两个数相乘,积是正数的概率是______.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为( )
A. B. C. D.
B
请用列表法写出所有可能的结果.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
随堂练习
小强
小华
剪刀
石头
布
剪刀
石头
布
(剪刀,剪刀)
(剪刀,石头)
(剪刀,布)
(石头,剪刀)
(石头,石头)
(石头,布)
(布,剪刀)
(布,石头)
(布,布)
小强和小华两人玩“剪刀、石头、布”游戏,随机出手一次,则两人平局的概率为
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
用直接列举法和列表法求概率
1.用列举法(列表法)求简单随机事件的概率.
3.适用条件:
如果事件中各种结果出现的可能性均等,含有两次操作(如掷骰子两次)或两个条件(如掷两个骰子)的事件.
2.用列表法求概率的步骤:
①列表;②通过表格计数,确定所有等可能的结果数n和关注的结果数m的值;③利用概率公式 计算出事件的概率.
布置作业
教科书第138页练习1、2.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
