人教版九年级数学上册24.1.4《圆周角》第2课时 教学课件(共16张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.4《圆周角》第2课时 教学课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 11:59:32 | ||
图片预览



文档简介
(共16张PPT)
24.1.4 圆周角
第2课时
学习目标
1.理解圆内接多边形的定义,掌握圆内接四边形的概念和性质;
2.能运用圆内接四边形的性质证明和计算;
3.经历圆内接四边形的性质的探究与证明,渗透“由特殊到一般”的数学思想方法;
4.通过学生自主探究、合作交流的学习过程,体验实现自身价值的愉悦和数学的应用.
圆周角
圆周角定理及其推论
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
回顾
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
直径是特殊的弦,对于一般的弦,它所对的圆周角是否也相等呢?
同圆或等圆中,同弦或等弦所对的圆周角相等吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
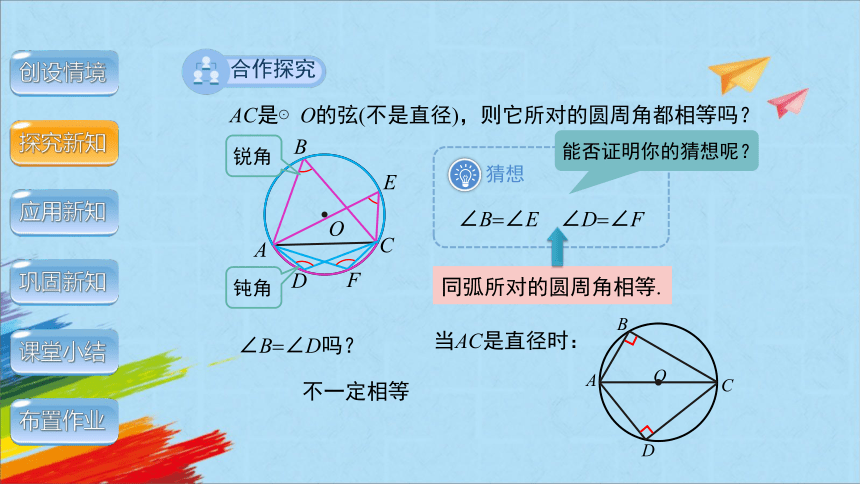
AC是⊙O的弦(不是直径),则它所对的圆周角都相等吗?
O
A
C
B
E
D
F
猜想
∠B ∠E
∠D ∠F
能否证明你的猜想呢?
同弧所对的圆周角相等.
∠B ∠D吗?
A
C
B
O
D
不一定相等
锐角
钝角
当AC是直径时:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
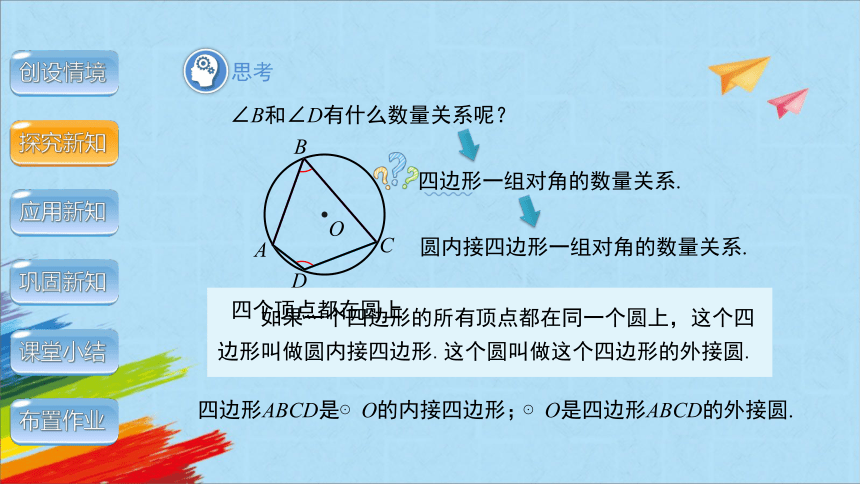
∠B和∠D有什么数量关系呢?
O
A
C
B
D
思考
四边形一组对角的数量关系.
四个顶点都在圆上
如果一个四边形的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.这个圆叫做这个四边形的外接圆.
圆内接四边形一组对角的数量关系.
四边形ABCD是⊙O的内接四边形;
⊙O是四边形ABCD的外接圆.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
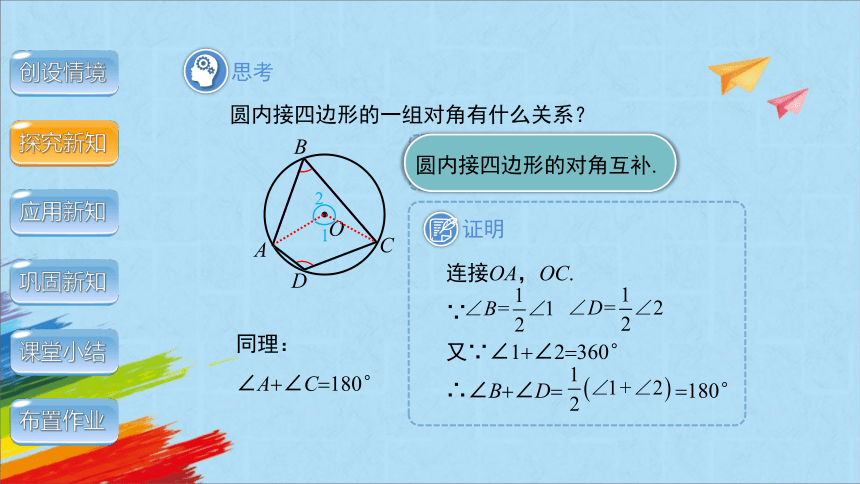
圆内接四边形的一组对角有什么关系?
O
A
C
B
D
思考
连接OA,OC.
∵
又∵∠1 ∠2 360°
∴∠B ∠D 180°
猜想
互补
1
2
证明
同理:
∠A ∠C 180°
圆内接四边形的对角互补.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
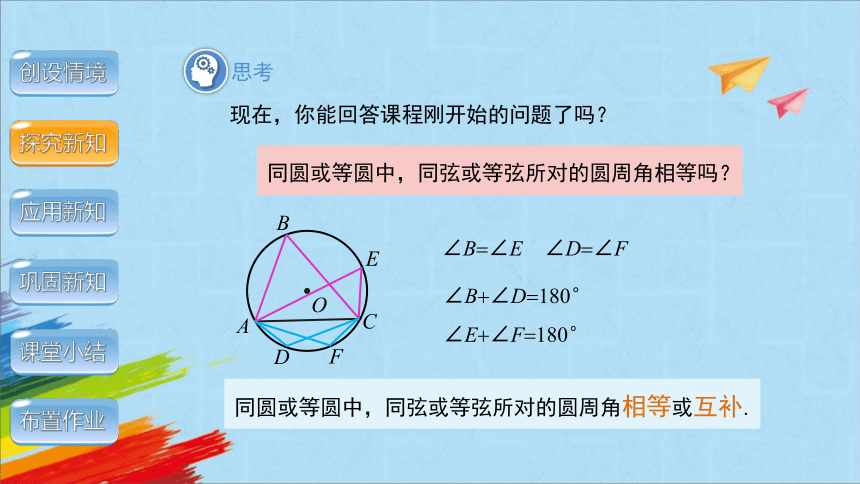
现在,你能回答课程刚开始的问题了吗?
思考
同圆或等圆中,同弦或等弦所对的圆周角相等吗?
O
A
C
B
E
D
F
∠B ∠E
∠D ∠F
∠B ∠D 180°
∠E ∠F 180°
同圆或等圆中,同弦或等弦所对的圆周角相等或互补.
延伸
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如图,四边形ABCD是⊙O的内接四边形;∠A与∠BCE有什么关系?
D
O
A
C
B
E
∠BCE ∠BCD 180°
∠BCD ∠A 180°
∠BCE ∠A
圆内接四边形的一个外角等于它的内对角.
延伸
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
圆内接四边形也可扩展到圆内接多边形.
D
O
A
C
B
E
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做这个多边形的外接圆.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1:如图,四边形ABCD是圆的内接四边形,且ABCD是平行四边形.求证:四边形ABCD是矩形.
解:∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
又∵四边形ABCD是圆的内接四边形
∴ ∠A ∠C 180°
∠B ∠D 180°
即:∠A=∠B ∠C=∠D 90°
∴四边形ABCD是矩形.
A
O
B
D
C
·
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
1.如图在圆内接四边形ABCD中,
(1)若∠B=30°,则∠D=_ _.
(2)若∠A∶∠C 5∶4,则∠A _ _.
150°
随堂练习
A
O
B
C
D
·
(1)∠B ∠D 180°
∠D 150°
100°
∠B 30°
(2)∠A ∠C 180°
∠A∶∠C 5∶4
∠A 180° 100°
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
2.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).
A.69° B.42° C.48° D.38°
随堂练习
∠BOD 138°
∠A 69°
∠A ∠DCB 180°
∠DCB ∠DCE 180°
∠A ∠DCE
A
O
B
C
D
·
E
69°
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
3.若ABCD为圆内接四边形,下列可能成立的是( )
A. ∠A∶∠B∶∠C∶∠D 1∶2∶3∶4
B. ∠A∶∠B∶∠C∶∠D 2∶1∶3∶4
C. ∠A∶∠B∶∠C∶∠D 3∶2∶1∶4
D. ∠A∶∠B∶∠C∶∠D 4∶3∶2∶1
随堂练习
A
O
B
C
D
·
B
比较∠A ∠C 和∠B ∠D所占的份数是否相等即可.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
概念
圆内接四边形
性质
延伸
圆内接四边形的对角互补.
圆内接四边形的一个外角等于它的内对角.
如果一个四边形的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.这个圆叫做这个四边形的外接圆.
布置作业
教科书第88页
练习第2、5题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
24.1.4 圆周角
第2课时
学习目标
1.理解圆内接多边形的定义,掌握圆内接四边形的概念和性质;
2.能运用圆内接四边形的性质证明和计算;
3.经历圆内接四边形的性质的探究与证明,渗透“由特殊到一般”的数学思想方法;
4.通过学生自主探究、合作交流的学习过程,体验实现自身价值的愉悦和数学的应用.
圆周角
圆周角定理及其推论
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
回顾
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
直径是特殊的弦,对于一般的弦,它所对的圆周角是否也相等呢?
同圆或等圆中,同弦或等弦所对的圆周角相等吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
AC是⊙O的弦(不是直径),则它所对的圆周角都相等吗?
O
A
C
B
E
D
F
猜想
∠B ∠E
∠D ∠F
能否证明你的猜想呢?
同弧所对的圆周角相等.
∠B ∠D吗?
A
C
B
O
D
不一定相等
锐角
钝角
当AC是直径时:
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
∠B和∠D有什么数量关系呢?
O
A
C
B
D
思考
四边形一组对角的数量关系.
四个顶点都在圆上
如果一个四边形的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.这个圆叫做这个四边形的外接圆.
圆内接四边形一组对角的数量关系.
四边形ABCD是⊙O的内接四边形;
⊙O是四边形ABCD的外接圆.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
圆内接四边形的一组对角有什么关系?
O
A
C
B
D
思考
连接OA,OC.
∵
又∵∠1 ∠2 360°
∴∠B ∠D 180°
猜想
互补
1
2
证明
同理:
∠A ∠C 180°
圆内接四边形的对角互补.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
现在,你能回答课程刚开始的问题了吗?
思考
同圆或等圆中,同弦或等弦所对的圆周角相等吗?
O
A
C
B
E
D
F
∠B ∠E
∠D ∠F
∠B ∠D 180°
∠E ∠F 180°
同圆或等圆中,同弦或等弦所对的圆周角相等或互补.
延伸
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如图,四边形ABCD是⊙O的内接四边形;∠A与∠BCE有什么关系?
D
O
A
C
B
E
∠BCE ∠BCD 180°
∠BCD ∠A 180°
∠BCE ∠A
圆内接四边形的一个外角等于它的内对角.
延伸
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
圆内接四边形也可扩展到圆内接多边形.
D
O
A
C
B
E
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做这个多边形的外接圆.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1:如图,四边形ABCD是圆的内接四边形,且ABCD是平行四边形.求证:四边形ABCD是矩形.
解:∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
又∵四边形ABCD是圆的内接四边形
∴ ∠A ∠C 180°
∠B ∠D 180°
即:∠A=∠B ∠C=∠D 90°
∴四边形ABCD是矩形.
A
O
B
D
C
·
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
1.如图在圆内接四边形ABCD中,
(1)若∠B=30°,则∠D=_ _.
(2)若∠A∶∠C 5∶4,则∠A _ _.
150°
随堂练习
A
O
B
C
D
·
(1)∠B ∠D 180°
∠D 150°
100°
∠B 30°
(2)∠A ∠C 180°
∠A∶∠C 5∶4
∠A 180° 100°
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
2.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).
A.69° B.42° C.48° D.38°
随堂练习
∠BOD 138°
∠A 69°
∠A ∠DCB 180°
∠DCB ∠DCE 180°
∠A ∠DCE
A
O
B
C
D
·
E
69°
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
3.若ABCD为圆内接四边形,下列可能成立的是( )
A. ∠A∶∠B∶∠C∶∠D 1∶2∶3∶4
B. ∠A∶∠B∶∠C∶∠D 2∶1∶3∶4
C. ∠A∶∠B∶∠C∶∠D 3∶2∶1∶4
D. ∠A∶∠B∶∠C∶∠D 4∶3∶2∶1
随堂练习
A
O
B
C
D
·
B
比较∠A ∠C 和∠B ∠D所占的份数是否相等即可.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
概念
圆内接四边形
性质
延伸
圆内接四边形的对角互补.
圆内接四边形的一个外角等于它的内对角.
如果一个四边形的所有顶点都在同一个圆上,这个四边形叫做圆内接四边形.这个圆叫做这个四边形的外接圆.
布置作业
教科书第88页
练习第2、5题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
