人教版九年级数学上册24.1.4《圆周角》第1课时 教学课件(共24张PPT)
文档属性
| 名称 | 人教版九年级数学上册24.1.4《圆周角》第1课时 教学课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
24.1.4 圆周角
第1课时
学习目标
1.了解圆周角的概念,会证明圆周角定理及其推论;
2.初步运用圆周角定理进行证明和计算;
3.经历圆周角定理的发现、探究与证明,使学生感悟分类讨论的数学思想,体会数学知识的一般形成过程;
4.通过学生自主探究圆周角的概念及定理,合作交流的学习过程,体验实现自身价值的愉悦和数学的应用.
圆周角
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
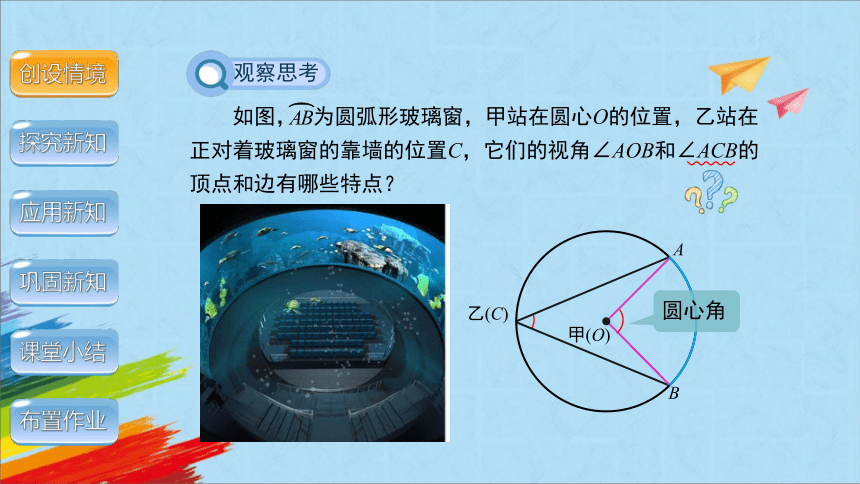
观察思考
如图, 为圆弧形玻璃窗,甲站在圆心O的位置,乙站在正对着玻璃窗的靠墙的位置C,它们的视角∠AOB和∠ACB的顶点和边有哪些特点?
A
B
甲(O)
乙(C)
圆心角
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
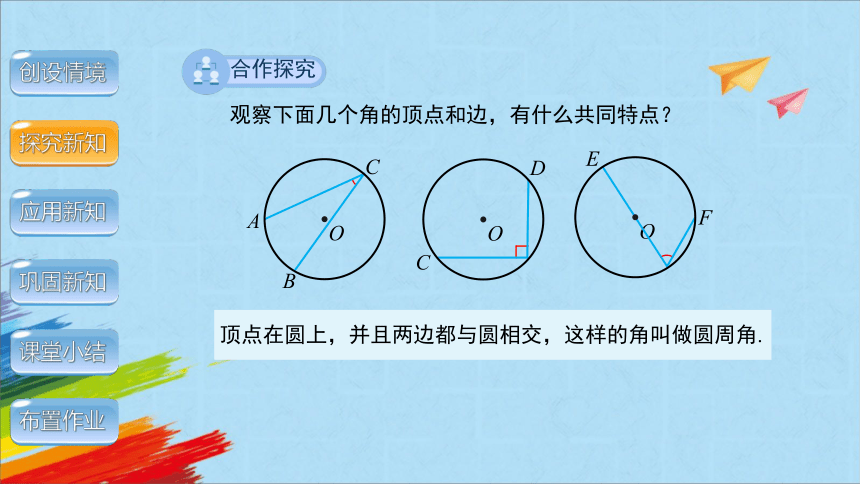
合作探究
观察下面几个角的顶点和边,有什么共同特点?
O
A
B
O
C
D
O
E
F
顶点在圆上,并且两边都与圆相交,这样的角叫做圆周角.
C
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
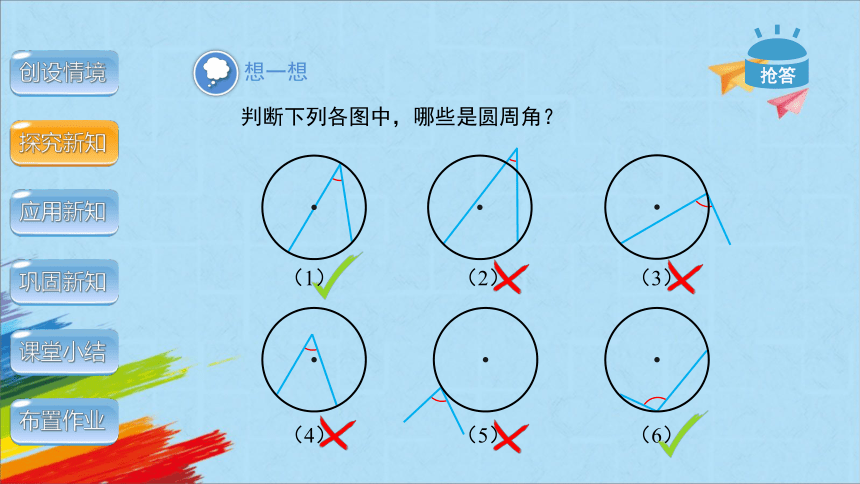
判断下列各图中,哪些是圆周角?
想一想
(1)
(2)
(3)
(4)
(5)
(6)
抢答
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
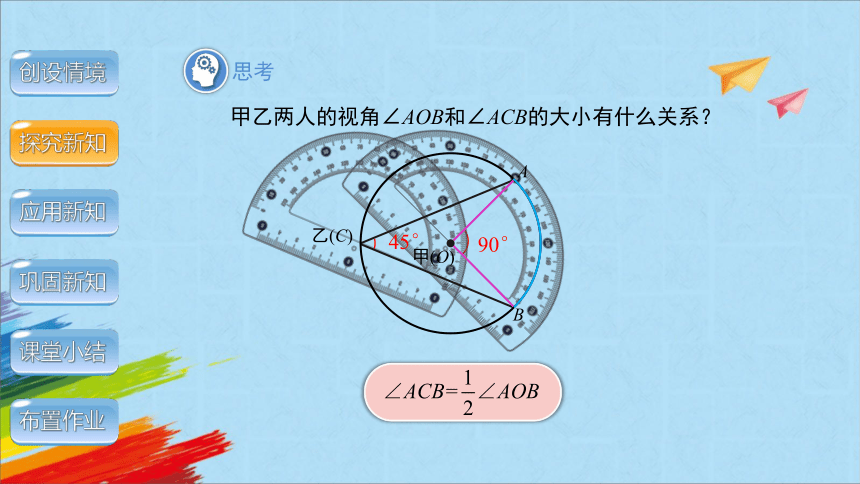
思考
甲乙两人的视角∠AOB和∠ACB的大小有什么关系?
90°
45°
A
B
甲(O)
乙(C)
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
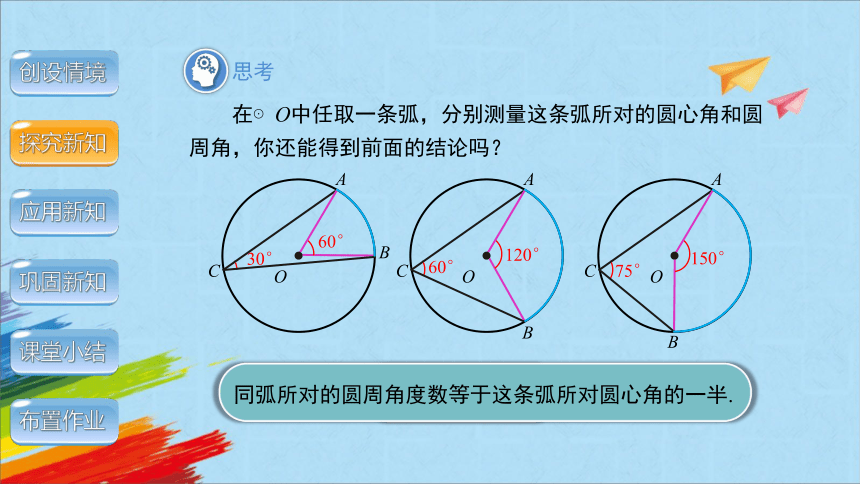
在⊙O中任取一条弧,分别测量这条弧所对的圆心角和圆周角,你还能得到前面的结论吗?
小组合作
1.两人一组,合作完成;
2.动手画图、测量,观察结果,总结规律.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
在⊙O中任取一条弧,分别测量这条弧所对的圆心角和圆周角,你还能得到前面的结论吗?
60°
30°
A
B
O
C
120°
60°
A
B
O
C
150°
75°
A
B
O
C
同弧所对的圆周角度数等于这条弧所对圆心角的一半.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
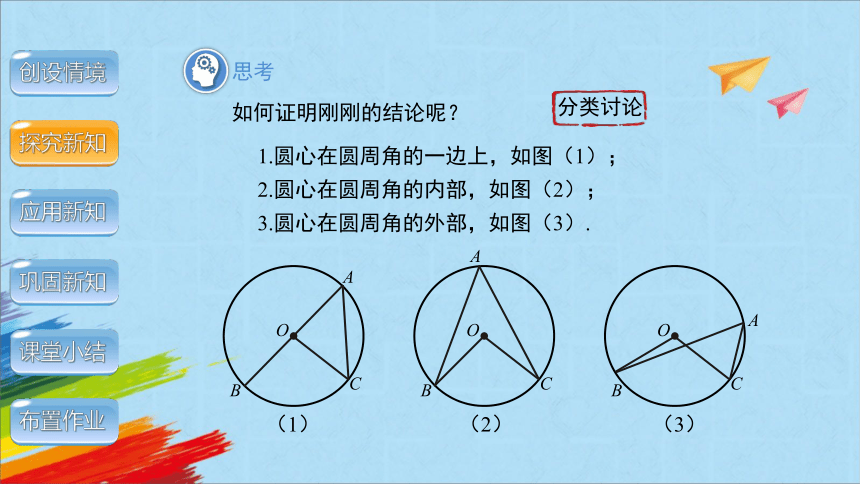
如何证明刚刚的结论呢?
1.圆心在圆周角的一边上,如图(1);
2.圆心在圆周角的内部,如图(2);
3.圆心在圆周角的外部,如图(3).
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
分类讨论
思考
证明
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
A
B
O
C
(1)
在第(1)种情况下,如何证明 ?
OA OC
∠A ∠C
∠BOC ∠A ∠C
尝试完成第(2)、(3)种情况的证明.
证明
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
A
B
O
C
(2)
D
OA OB OC
∠3 ∠4 ∠B ∠C
∠1 ∠B ∠3
1
2
3
4
2∠3
∠2 ∠C ∠4
2∠4
∠1 ∠2
2(∠3 ∠4)
2∠BAC
∠BOC
A
B
O
C
(3)
D
1
2
OA OB OC
∠2 ∠B,∠OAC ∠C
∠1 ∠B ∠2
2∠2
∠DOC
2∠OAC
∠DOC ∠1
2(∠OAC ∠2)
2∠BAC
∠BOC
∠C ∠OAC
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
A
B
C
O
D
E
小组合作
1.猜想可能的结果;
2.验证你的猜想.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
A
B
C
O
D
E
∠BAC ∠BDC ∠BEC
∠BAC ∠BDC ∠BEC
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
∠ADC ∠BAD
推论1:同弧或等弧所对的圆周角相等.
等弧
B
A
O
D
C
∠AOC ∠BOD
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如图,AB是直径,C是圆上任意一点(不与A、B重合),求∠ACB °.
A
B
C
O
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
做一做
90
180°
如果∠ACB 90°,能得出AB是直径吗?
圆周角定理及其推论
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1:如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
A
O
B
D
C
·
6
10
解:连接OD,∵AB是直径
∴∠ACB=∠ADB=90°.
在Rt△ABC中,
又∵CD平分∠ACB,∴∠ACD ∠BCD
∴AD BD
在Rt△ABD中,AD2 BD2 AB2
∴AD BD AB 10
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
1.如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=___.
50°
随堂练习
A
O
B
C
D
·
AB是直径
∠ADB 90°
∠BCD ∠BAD
∠ABD 40°
∠BAD 50°
50°
40°
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
2.在⊙O中,∠CBD=30°,∠BDC=20°,求∠A.
随堂练习
B
O
D
C
·
A
B
O
D
C
·
A
∠CAD=∠CBD=30°
∠BAC=∠BDC=20°
∠A ∠CAD ∠BAC=50°
∠BOC=2∠BDC=40°
∠COD=2∠CBD=60°
∠BOD ∠BOC ∠COD=100°
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
3.如图,在⊙O中,AB为直径, ,弦CG⊥AB,交AB于D,交BF于E.求证:BE=EC.
随堂练习
B
O
D
C
·
F
G
A
E
证明:连接CB,
∵AB为直径,弦CG⊥AB,
∴
又∵
∴
∴∠CBF=∠BCG
∴ BE=EC
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
概念
圆周角
圆周角定理
推论
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
布置作业
教科书第88页
练习第1、3题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
24.1.4 圆周角
第1课时
学习目标
1.了解圆周角的概念,会证明圆周角定理及其推论;
2.初步运用圆周角定理进行证明和计算;
3.经历圆周角定理的发现、探究与证明,使学生感悟分类讨论的数学思想,体会数学知识的一般形成过程;
4.通过学生自主探究圆周角的概念及定理,合作交流的学习过程,体验实现自身价值的愉悦和数学的应用.
圆周角
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察思考
如图, 为圆弧形玻璃窗,甲站在圆心O的位置,乙站在正对着玻璃窗的靠墙的位置C,它们的视角∠AOB和∠ACB的顶点和边有哪些特点?
A
B
甲(O)
乙(C)
圆心角
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
观察下面几个角的顶点和边,有什么共同特点?
O
A
B
O
C
D
O
E
F
顶点在圆上,并且两边都与圆相交,这样的角叫做圆周角.
C
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
判断下列各图中,哪些是圆周角?
想一想
(1)
(2)
(3)
(4)
(5)
(6)
抢答
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
甲乙两人的视角∠AOB和∠ACB的大小有什么关系?
90°
45°
A
B
甲(O)
乙(C)
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
在⊙O中任取一条弧,分别测量这条弧所对的圆心角和圆周角,你还能得到前面的结论吗?
小组合作
1.两人一组,合作完成;
2.动手画图、测量,观察结果,总结规律.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
在⊙O中任取一条弧,分别测量这条弧所对的圆心角和圆周角,你还能得到前面的结论吗?
60°
30°
A
B
O
C
120°
60°
A
B
O
C
150°
75°
A
B
O
C
同弧所对的圆周角度数等于这条弧所对圆心角的一半.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如何证明刚刚的结论呢?
1.圆心在圆周角的一边上,如图(1);
2.圆心在圆周角的内部,如图(2);
3.圆心在圆周角的外部,如图(3).
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
分类讨论
思考
证明
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
A
B
O
C
(1)
在第(1)种情况下,如何证明 ?
OA OC
∠A ∠C
∠BOC ∠A ∠C
尝试完成第(2)、(3)种情况的证明.
证明
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
A
B
O
C
(2)
D
OA OB OC
∠3 ∠4 ∠B ∠C
∠1 ∠B ∠3
1
2
3
4
2∠3
∠2 ∠C ∠4
2∠4
∠1 ∠2
2(∠3 ∠4)
2∠BAC
∠BOC
A
B
O
C
(3)
D
1
2
OA OB OC
∠2 ∠B,∠OAC ∠C
∠1 ∠B ∠2
2∠2
∠DOC
2∠OAC
∠DOC ∠1
2(∠OAC ∠2)
2∠BAC
∠BOC
∠C ∠OAC
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
O
C
(1)
A
B
O
C
(2)
A
B
O
C
(3)
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
A
B
C
O
D
E
小组合作
1.猜想可能的结果;
2.验证你的猜想.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
A
B
C
O
D
E
∠BAC ∠BDC ∠BEC
∠BAC ∠BDC ∠BEC
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
“在同圆或等圆中,同弧所对的圆心角相等”那么同弧所对的圆周角呢?
∠ADC ∠BAD
推论1:同弧或等弧所对的圆周角相等.
等弧
B
A
O
D
C
∠AOC ∠BOD
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如图,AB是直径,C是圆上任意一点(不与A、B重合),求∠ACB °.
A
B
C
O
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
做一做
90
180°
如果∠ACB 90°,能得出AB是直径吗?
圆周角定理及其推论
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1:如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
A
O
B
D
C
·
6
10
解:连接OD,∵AB是直径
∴∠ACB=∠ADB=90°.
在Rt△ABC中,
又∵CD平分∠ACB,∴∠ACD ∠BCD
∴AD BD
在Rt△ABD中,AD2 BD2 AB2
∴AD BD AB 10
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
1.如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=___.
50°
随堂练习
A
O
B
C
D
·
AB是直径
∠ADB 90°
∠BCD ∠BAD
∠ABD 40°
∠BAD 50°
50°
40°
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
2.在⊙O中,∠CBD=30°,∠BDC=20°,求∠A.
随堂练习
B
O
D
C
·
A
B
O
D
C
·
A
∠CAD=∠CBD=30°
∠BAC=∠BDC=20°
∠A ∠CAD ∠BAC=50°
∠BOC=2∠BDC=40°
∠COD=2∠CBD=60°
∠BOD ∠BOC ∠COD=100°
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
3.如图,在⊙O中,AB为直径, ,弦CG⊥AB,交AB于D,交BF于E.求证:BE=EC.
随堂练习
B
O
D
C
·
F
G
A
E
证明:连接CB,
∵AB为直径,弦CG⊥AB,
∴
又∵
∴
∴∠CBF=∠BCG
∴ BE=EC
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
概念
圆周角
圆周角定理
推论
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
一条弧所对的圆周角等于它所对的圆心角的一半.
推论1:同弧或等弧所对的圆周角相等.
推论2:半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
布置作业
教科书第88页
练习第1、3题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
