人教版九年级数学上册23.2.1《中心对称图形》教学课件(共25张PPT)
文档属性
| 名称 | 人教版九年级数学上册23.2.1《中心对称图形》教学课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 12:30:32 | ||
图片预览


文档简介
(共25张PPT)
23.2.2 中心对称图形
学习目标
1.了解中心对称图形的概念,能够判断一个图形是否为中心对称图形.
2.能够判断出中心对称图形的对称中心,能够区分中心对称图形.
3.通过观察、交流等活动,培养学生的概括能力和实践能力.
4.经历观察生活中的中心对称图形,让学生感受现实生活中数学的美,激发学生学习数学的兴趣,培养学生热爱生活的情操.
中心对称图形
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
A
C
A′
C′
O
B
B′
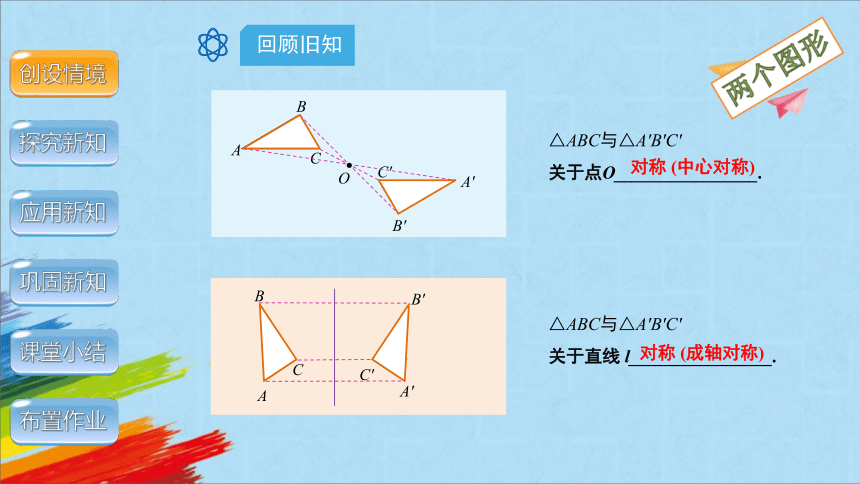
△ABC与△A′B′C′
关于点O________________.
△ABC与△A′B′C′
关于直线 l________________.
A
C
B
A′
C′
B′
对称 (中心对称)
对称 (成轴对称)
两个图形
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
A
C
B
D
E
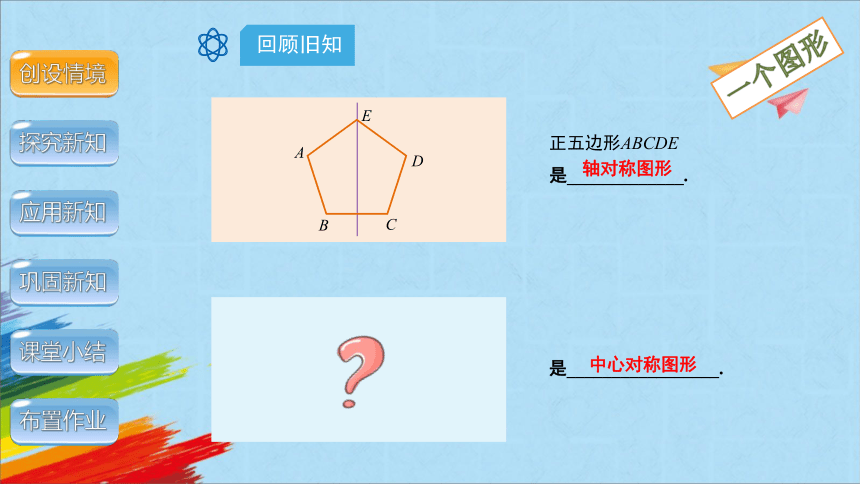
正五边形ABCDE
是_____________.
轴对称图形
是_________________.
一个图形
中心对称图形
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
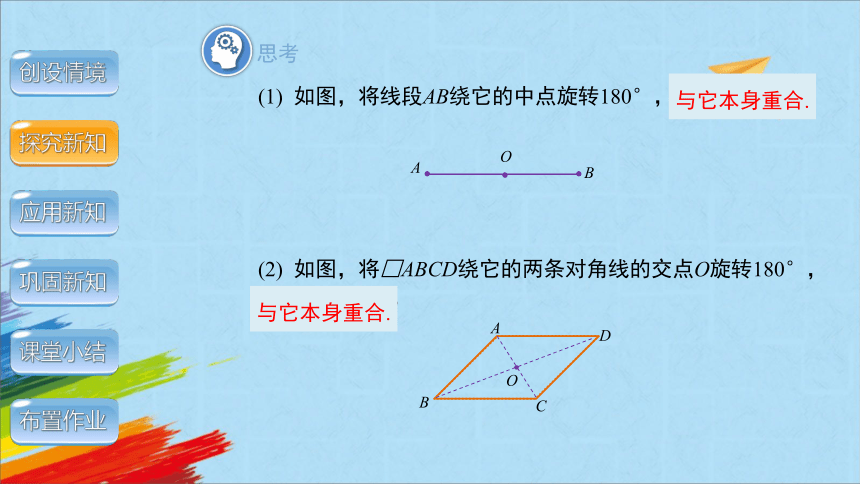
(1) 如图,将线段AB绕它的中点旋转180°,你有什么发现?
A
B
O
(2) 如图,将□ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
与它本身重合.
与它本身重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
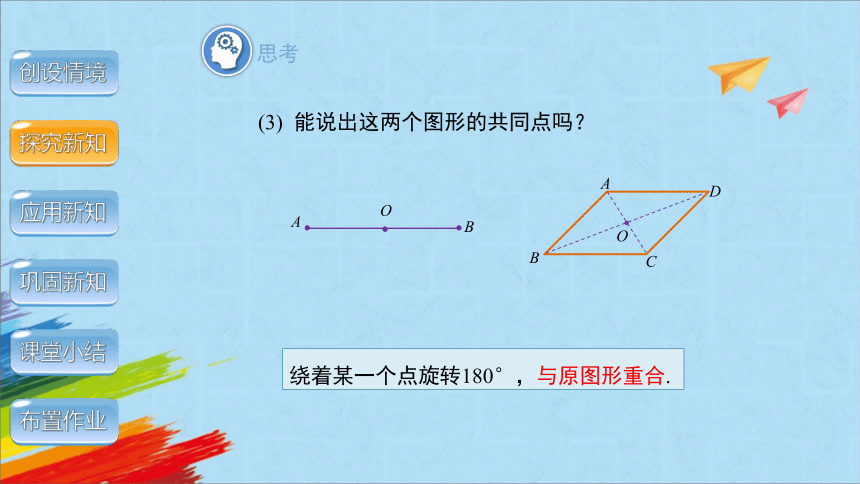
(3) 能说出这两个图形的共同点吗?
A
B
O
A
B
C
D
O
绕着某一个点旋转180°,与原图形重合.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
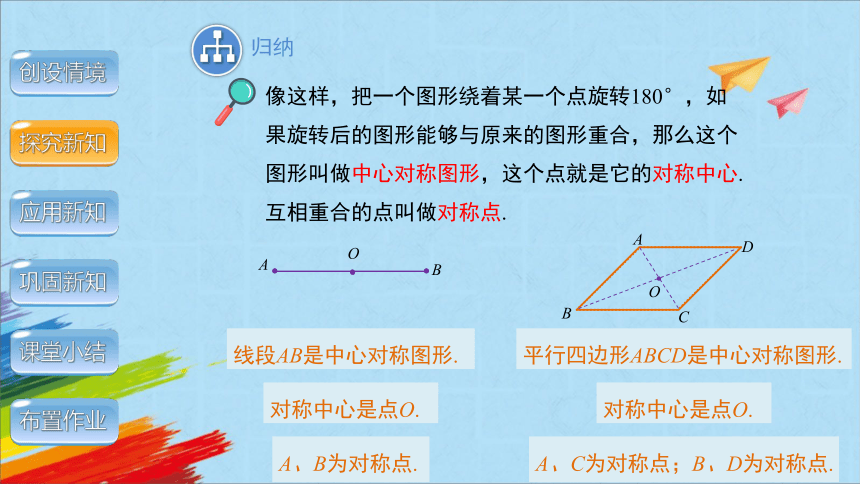
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
互相重合的点叫做对称点.
A
B
O
A
B
C
D
O
线段AB是中心对称图形.
对称中心是点O.
平行四边形ABCD是中心对称图形.
对称中心是点O.
A、B为对称点.
A、C为对称点;B、D为对称点.
应用新知
巩固新知
课堂小结
布置作业
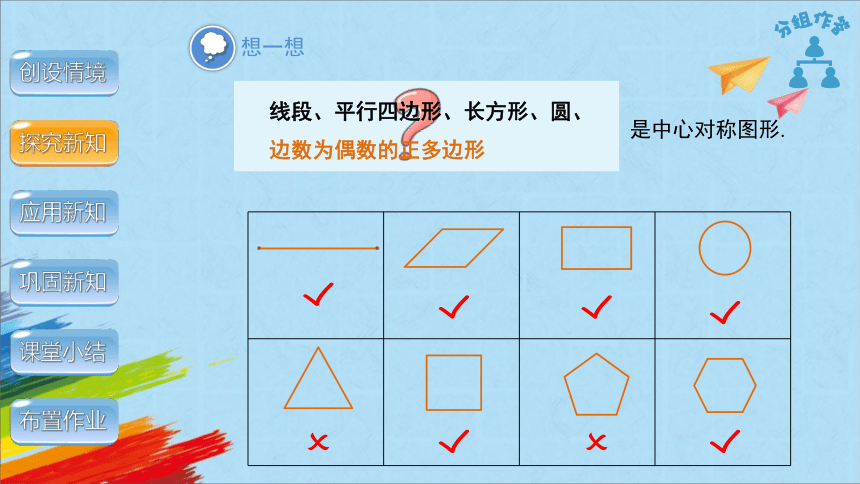
是中心对称图形.
想一想
线段、平行四边形、长方形、圆、
边数为偶数的正多边形
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
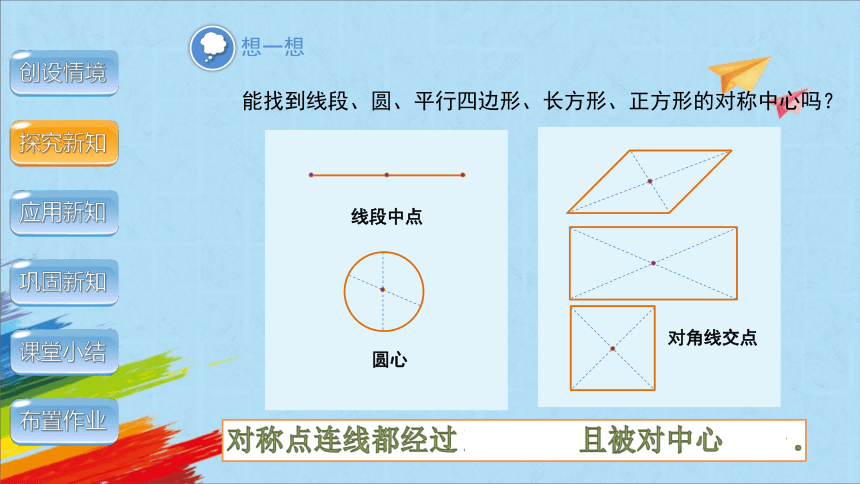
想一想
能找到线段、圆、平行四边形、长方形、正方形的对称中心吗?
线段中点
圆心
创设情境
探究新知
对角线交点
对称点连线都经过 对称中心且被对中心 平分 .
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
说说生活中常见到的中心对称图形
交流
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
判断下列图形是不是中心对称图形?
做一做
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
下列图形是中心对称图形吗?如果是,请指出对称中心.
做一做
(1)
(2)
(3)
(4)
中心对称图形顺时针、逆时针旋转180°都重合
都是中心对称图形.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
中心对称与中心对称图形的区别与联系?
中心对称图形
中心对称
____个图形之间的关系.
具有某种性质的___个图形.
若把中心对称图形的两部分分别看作两个图形,则它们成________.
区别
联系
对称点分别在___个图形上.
对称点在______个图形上.
若把中心对称的两个图形看作一个整体,则成为______________.
对称中心在___个图形之间.
对称中心在图形___或其_____.
中心对称和中心对称图形都是绕着某一点进行________后_____.
归纳
旋转180°
重合
中心对称
中心对称图形
两
一
两
同一
两
上
内部
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
中心对称图形与轴对称图形的区别与联系?
中心对称图形
轴对称图形
有一条对称轴——_____.
有一个对称中心——___.
图形沿_________________.
图形绕_______________________.
翻转后图形两部分________.
旋转前后的图形_________.
1
2
3
归纳
直线
点
轴对折(翻转180°)
对称中心旋转(旋转180°)
完全重合
完全重合
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
将两个大小相等的圆部分重合,其中重叠的部分(如下图的阴影部分)我们称之为一个“花瓣”,由一个“花瓣”及圆组成的图形称之为花瓣图形,下面是一些由“花瓣”和圆组成的图形.
A.
二瓣
B.
三瓣
C.
四瓣
D.
五瓣
E.
六瓣
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
(1) 以上5个图形中是轴对称图形的有_____________,是中心对称图形的有_______;(分别用图形的代号A、B、C、D、E填空).
(2) 若“花瓣”在圆中是均匀分布的,试根据上题的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)之间的规律:______________________________________________
A.
二瓣
B.
三瓣
C.
四瓣
D.
五瓣
E.
六瓣
A、B、C、D、E
A、C、E
“花瓣”个数为偶数时,这个图形既是轴对称图形又是中心对称图形;“花瓣”个数为奇数时,这个图形是轴对称图形.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
判断下列说法是否正确.
(1)轴对称图形也是中心对称图形.( )
(2)旋转对称图形也是中心对称图形.( )
(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交
点是它们的对称中心.( )
(4)角是轴对称图形也是中心对称图形.( )
(5)在成中心对称的两个图形中,对应线段平行(或在同一直线
上)且相等. ( )
×
√
×
√
×
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
选择题:
下列多边形中,是中心对称图形而不是轴对称图形的是( )
平行四边形
B. 矩形
C. 菱形
D. 正方形
A
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
下面的扑克牌中,哪些牌面是中心对称图形?
应用新知
课堂小结
布置作业
创设情境
练习4
随堂练习
探究新知
巩固新知
在26个英文大写正体字母中,哪些字母是中心对称图形?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
图形
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
互相重合的点叫做对称点.
对称点连线都经过对称中心且被对称中心平分 .
定义
性质
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
图形
中心对称与中心对称图形的区别与联系
中心对称图形
中心对称
两个图形之间的关系.
具有某种性质的一个图形.
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称.
区别
联系
对称点分别在两个图形上.
对称点在同一个图形上.
若把中心对称的两个图形看作一个整体,则成为中心对称图形.
对称中心在两个图形之间.
对称中心在图形上或其内部.
中心对称和中心对称图形都是绕着某一点进行旋转180°后重合.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
图形
中心对称图形与轴对称图形的区别与联系
中心对称图形
轴对称图形
有一条对称轴——直线.
有一个对称中心——点.
图形沿轴对折(翻转180°).
图形绕对称中心旋转(旋转180°).
翻转后图形两部分完全重合.
旋转前后的图形完全重合.
1
2
3
布置作业
教科书第69页,习题2.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
23.2.2 中心对称图形
学习目标
1.了解中心对称图形的概念,能够判断一个图形是否为中心对称图形.
2.能够判断出中心对称图形的对称中心,能够区分中心对称图形.
3.通过观察、交流等活动,培养学生的概括能力和实践能力.
4.经历观察生活中的中心对称图形,让学生感受现实生活中数学的美,激发学生学习数学的兴趣,培养学生热爱生活的情操.
中心对称图形
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
A
C
A′
C′
O
B
B′
△ABC与△A′B′C′
关于点O________________.
△ABC与△A′B′C′
关于直线 l________________.
A
C
B
A′
C′
B′
对称 (中心对称)
对称 (成轴对称)
两个图形
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾旧知
A
C
B
D
E
正五边形ABCDE
是_____________.
轴对称图形
是_________________.
一个图形
中心对称图形
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
(1) 如图,将线段AB绕它的中点旋转180°,你有什么发现?
A
B
O
(2) 如图,将□ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
与它本身重合.
与它本身重合.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
(3) 能说出这两个图形的共同点吗?
A
B
O
A
B
C
D
O
绕着某一个点旋转180°,与原图形重合.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
互相重合的点叫做对称点.
A
B
O
A
B
C
D
O
线段AB是中心对称图形.
对称中心是点O.
平行四边形ABCD是中心对称图形.
对称中心是点O.
A、B为对称点.
A、C为对称点;B、D为对称点.
应用新知
巩固新知
课堂小结
布置作业
是中心对称图形.
想一想
线段、平行四边形、长方形、圆、
边数为偶数的正多边形
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
想一想
能找到线段、圆、平行四边形、长方形、正方形的对称中心吗?
线段中点
圆心
创设情境
探究新知
对角线交点
对称点连线都经过 对称中心且被对中心 平分 .
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
说说生活中常见到的中心对称图形
交流
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
判断下列图形是不是中心对称图形?
做一做
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
下列图形是中心对称图形吗?如果是,请指出对称中心.
做一做
(1)
(2)
(3)
(4)
中心对称图形顺时针、逆时针旋转180°都重合
都是中心对称图形.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
中心对称与中心对称图形的区别与联系?
中心对称图形
中心对称
____个图形之间的关系.
具有某种性质的___个图形.
若把中心对称图形的两部分分别看作两个图形,则它们成________.
区别
联系
对称点分别在___个图形上.
对称点在______个图形上.
若把中心对称的两个图形看作一个整体,则成为______________.
对称中心在___个图形之间.
对称中心在图形___或其_____.
中心对称和中心对称图形都是绕着某一点进行________后_____.
归纳
旋转180°
重合
中心对称
中心对称图形
两
一
两
同一
两
上
内部
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
中心对称图形与轴对称图形的区别与联系?
中心对称图形
轴对称图形
有一条对称轴——_____.
有一个对称中心——___.
图形沿_________________.
图形绕_______________________.
翻转后图形两部分________.
旋转前后的图形_________.
1
2
3
归纳
直线
点
轴对折(翻转180°)
对称中心旋转(旋转180°)
完全重合
完全重合
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
将两个大小相等的圆部分重合,其中重叠的部分(如下图的阴影部分)我们称之为一个“花瓣”,由一个“花瓣”及圆组成的图形称之为花瓣图形,下面是一些由“花瓣”和圆组成的图形.
A.
二瓣
B.
三瓣
C.
四瓣
D.
五瓣
E.
六瓣
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
(1) 以上5个图形中是轴对称图形的有_____________,是中心对称图形的有_______;(分别用图形的代号A、B、C、D、E填空).
(2) 若“花瓣”在圆中是均匀分布的,试根据上题的结果总结“花瓣”的个数与花瓣图形的对称性(轴对称或中心对称)之间的规律:______________________________________________
A.
二瓣
B.
三瓣
C.
四瓣
D.
五瓣
E.
六瓣
A、B、C、D、E
A、C、E
“花瓣”个数为偶数时,这个图形既是轴对称图形又是中心对称图形;“花瓣”个数为奇数时,这个图形是轴对称图形.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
判断下列说法是否正确.
(1)轴对称图形也是中心对称图形.( )
(2)旋转对称图形也是中心对称图形.( )
(3)平行四边形、长方形和正方形都是中心对称图形,对角线的交
点是它们的对称中心.( )
(4)角是轴对称图形也是中心对称图形.( )
(5)在成中心对称的两个图形中,对应线段平行(或在同一直线
上)且相等. ( )
×
√
×
√
×
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
选择题:
下列多边形中,是中心对称图形而不是轴对称图形的是( )
平行四边形
B. 矩形
C. 菱形
D. 正方形
A
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
下面的扑克牌中,哪些牌面是中心对称图形?
应用新知
课堂小结
布置作业
创设情境
练习4
随堂练习
探究新知
巩固新知
在26个英文大写正体字母中,哪些字母是中心对称图形?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
图形
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
互相重合的点叫做对称点.
对称点连线都经过对称中心且被对称中心平分 .
定义
性质
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
图形
中心对称与中心对称图形的区别与联系
中心对称图形
中心对称
两个图形之间的关系.
具有某种性质的一个图形.
若把中心对称图形的两部分分别看作两个图形,则它们成中心对称.
区别
联系
对称点分别在两个图形上.
对称点在同一个图形上.
若把中心对称的两个图形看作一个整体,则成为中心对称图形.
对称中心在两个图形之间.
对称中心在图形上或其内部.
中心对称和中心对称图形都是绕着某一点进行旋转180°后重合.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
中心对称
图形
中心对称图形与轴对称图形的区别与联系
中心对称图形
轴对称图形
有一条对称轴——直线.
有一个对称中心——点.
图形沿轴对折(翻转180°).
图形绕对称中心旋转(旋转180°).
翻转后图形两部分完全重合.
旋转前后的图形完全重合.
1
2
3
布置作业
教科书第69页,习题2.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
