人教版八年级数学上册13.2.1画轴对称图形 第2课时 教案(表格式)
文档属性
| 名称 | 人教版八年级数学上册13.2.1画轴对称图形 第2课时 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 572.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 16:12:59 | ||
图片预览


文档简介
第十三章 轴对称
13. 2画轴对称图形
第2课时
一、教学目标
1. 探究直角坐标系中关于x轴、y轴对称点的坐标变化规律;
2. 如何利用坐标的变化规律在平面直角坐标系中画出一个图形的轴对称图形;
3. 培养学生观察归纳能力,运用数形结合的方法,把坐标与图形的变换联系起来,体味几何图形的趣味性和数学内容的深刻性.
二、教学重难点
重点:探究直角坐标系中关于x轴、y轴对称点的坐标变化规律.
难点:如何利用坐标的变化规律在平面直角坐标系中画出一个图形的轴对称图形.
三、教学用具
直尺,白纸,多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
环节一创设情境 【观察思考】 下图是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,根据如图所示的东直门的坐标,你能说出西直门的坐标吗? 答:因为西直门和东直门是关于中轴线对称的,根据轴对称的性质,西直门的坐标为(3.5,4) 回答问题 回顾旧知识,对下一步探索新知识作铺垫
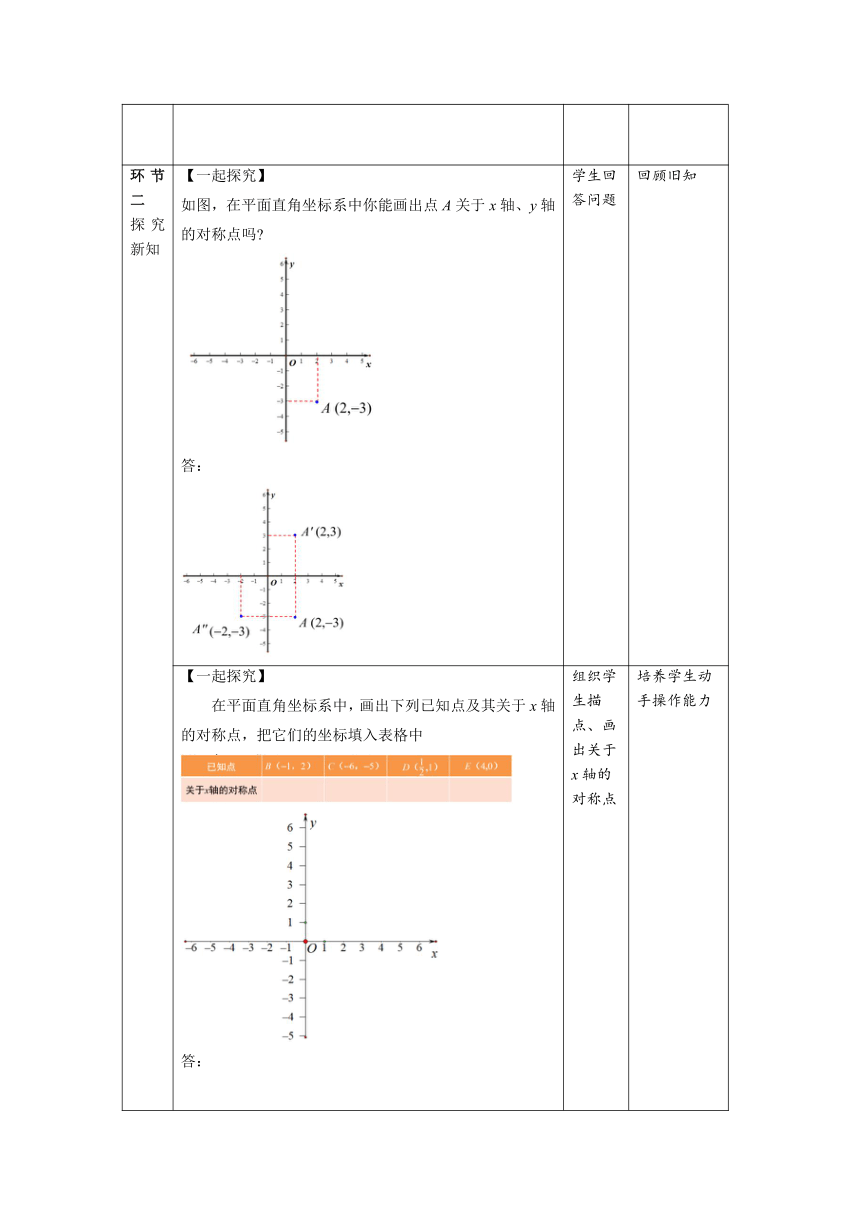
环节二 探究新知 【一起探究】 如图,在平面直角坐标系中你能画出点A关于x轴、y轴的对称点吗 答: 学生回答问题 回顾旧知
【一起探究】 在平面直角坐标系中,画出下列已知点及其关于x轴的对称点,把它们的坐标填入表格中 答: 【想一想】 观察下图中关于x轴对称的每对对称点的坐标有怎样的变化规律? 答:关于x轴对称的每对对称点的横坐标相等,纵坐标互为相反数。 【一起探究】 在平面直角坐标系中,画出下列已知点及其关于y轴的对称点,把它们的坐标填入表格中? 答: 【想一想】 观察下图中关于y轴对称的每对对称点的坐标有怎样的变化规律? 答:关于y轴对称的每对对称点的纵坐标相等,横坐标互为相反数。 【一起探究】 再找几个点,分别画出它们的对称点,检验一下你发现的规律 总结:点(x,y)关于x轴对称的点的坐标为(x,-y) 点(x,y)关于y轴对称的点的坐标为(-x,y) 【随堂练习】 1.点P(,6)与点Q关于x轴对称,则点Q的坐标为_ ______. 2.点M(a,5)与点N(2,b)关于x轴对称,则a= ___,b =_ __. 3.点P(5, 6)与点Q关于y轴对称,则点Q的坐标___ ____ 4.点M(a, 5)与点N(2, b)关于y轴对称,则a= ____, b =_ ____. 组织学生描点、画出关于x轴的对称点 小组讨论,观察各个对称点与原来点之间的坐标之间的关系 组织学生描点、画出关于y轴的对称点 小组讨论,观察各个对称点与原来点之间的坐标之间的关系 总结归纳,关于x轴、y轴对称的点的坐标特点 学生抢答 培养学生动手操作能力 培养学生运用数形结合的方法,及观察归纳能力. 培养学生动手操作能力 巩固所讲规律
环节三 应用新知 【典型例题】 例:如图,四边形ABCD 的四个顶点的坐标分别为 A(5,1),B(2,1),C(2,5),D(5,4),分别画出与四边形ABCD 关于y轴和x轴对称的图形. 解:点(x,y)关于y轴对称的点的坐标为(x,y),因此四边形ABCD 的顶点A,B,C,D 关于y轴对称的点分别为: A'(5,1) B'(2,1) C'(2,5) D'(5,4) 依次连接_____,_____ , _____, _____,就可得到与四边形ABCD关于y轴对称的四边形_________ 应用规律,进行解题,求出关于y轴对称点的坐标,并连线. 应用结论解决问题,培养学生独立思考的能力 教师引导学生,四边形由四个顶点连线形成,作出点关于坐标轴的对称点后,进行连线,即可求解。
环节三 应用新知 解:点(x,y)关于x轴对称的点的坐标为(x,y),因此四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为: A′'(5,1)B′'(2,1)C′'(2,5)D′'(5,4) 依次连接_____,______ , _____, _____,就可得到与四边形ABCD关于x轴对称的四边形_________ 应用规律,求出关于x轴点的坐标,并连线. 对本节课总结的规律,进行应用,巩固所学知识,让学生深入理解关于x轴、y轴对称点的特点
环节四 巩固新知 如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C'的坐标是(A) A.(3,1) B. (3,1) C.(1,3) D.(3,1) 学生回答问题 培养学生对知识的迁移能力,学会对问题进行转化的思维
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 教科书第70、71页习题1、2、3 71、72页第2、3、4题 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
13. 2画轴对称图形
第2课时
一、教学目标
1. 探究直角坐标系中关于x轴、y轴对称点的坐标变化规律;
2. 如何利用坐标的变化规律在平面直角坐标系中画出一个图形的轴对称图形;
3. 培养学生观察归纳能力,运用数形结合的方法,把坐标与图形的变换联系起来,体味几何图形的趣味性和数学内容的深刻性.
二、教学重难点
重点:探究直角坐标系中关于x轴、y轴对称点的坐标变化规律.
难点:如何利用坐标的变化规律在平面直角坐标系中画出一个图形的轴对称图形.
三、教学用具
直尺,白纸,多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
环节一创设情境 【观察思考】 下图是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,根据如图所示的东直门的坐标,你能说出西直门的坐标吗? 答:因为西直门和东直门是关于中轴线对称的,根据轴对称的性质,西直门的坐标为(3.5,4) 回答问题 回顾旧知识,对下一步探索新知识作铺垫
环节二 探究新知 【一起探究】 如图,在平面直角坐标系中你能画出点A关于x轴、y轴的对称点吗 答: 学生回答问题 回顾旧知
【一起探究】 在平面直角坐标系中,画出下列已知点及其关于x轴的对称点,把它们的坐标填入表格中 答: 【想一想】 观察下图中关于x轴对称的每对对称点的坐标有怎样的变化规律? 答:关于x轴对称的每对对称点的横坐标相等,纵坐标互为相反数。 【一起探究】 在平面直角坐标系中,画出下列已知点及其关于y轴的对称点,把它们的坐标填入表格中? 答: 【想一想】 观察下图中关于y轴对称的每对对称点的坐标有怎样的变化规律? 答:关于y轴对称的每对对称点的纵坐标相等,横坐标互为相反数。 【一起探究】 再找几个点,分别画出它们的对称点,检验一下你发现的规律 总结:点(x,y)关于x轴对称的点的坐标为(x,-y) 点(x,y)关于y轴对称的点的坐标为(-x,y) 【随堂练习】 1.点P(,6)与点Q关于x轴对称,则点Q的坐标为_ ______. 2.点M(a,5)与点N(2,b)关于x轴对称,则a= ___,b =_ __. 3.点P(5, 6)与点Q关于y轴对称,则点Q的坐标___ ____ 4.点M(a, 5)与点N(2, b)关于y轴对称,则a= ____, b =_ ____. 组织学生描点、画出关于x轴的对称点 小组讨论,观察各个对称点与原来点之间的坐标之间的关系 组织学生描点、画出关于y轴的对称点 小组讨论,观察各个对称点与原来点之间的坐标之间的关系 总结归纳,关于x轴、y轴对称的点的坐标特点 学生抢答 培养学生动手操作能力 培养学生运用数形结合的方法,及观察归纳能力. 培养学生动手操作能力 巩固所讲规律
环节三 应用新知 【典型例题】 例:如图,四边形ABCD 的四个顶点的坐标分别为 A(5,1),B(2,1),C(2,5),D(5,4),分别画出与四边形ABCD 关于y轴和x轴对称的图形. 解:点(x,y)关于y轴对称的点的坐标为(x,y),因此四边形ABCD 的顶点A,B,C,D 关于y轴对称的点分别为: A'(5,1) B'(2,1) C'(2,5) D'(5,4) 依次连接_____,_____ , _____, _____,就可得到与四边形ABCD关于y轴对称的四边形_________ 应用规律,进行解题,求出关于y轴对称点的坐标,并连线. 应用结论解决问题,培养学生独立思考的能力 教师引导学生,四边形由四个顶点连线形成,作出点关于坐标轴的对称点后,进行连线,即可求解。
环节三 应用新知 解:点(x,y)关于x轴对称的点的坐标为(x,y),因此四边形ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为: A′'(5,1)B′'(2,1)C′'(2,5)D′'(5,4) 依次连接_____,______ , _____, _____,就可得到与四边形ABCD关于x轴对称的四边形_________ 应用规律,求出关于x轴点的坐标,并连线. 对本节课总结的规律,进行应用,巩固所学知识,让学生深入理解关于x轴、y轴对称点的特点
环节四 巩固新知 如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C'的坐标是(A) A.(3,1) B. (3,1) C.(1,3) D.(3,1) 学生回答问题 培养学生对知识的迁移能力,学会对问题进行转化的思维
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 教科书第70、71页习题1、2、3 71、72页第2、3、4题 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
