人教版八年级数学上册 15.1.1 从分数到分式 教学课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册 15.1.1 从分数到分式 教学课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 16:34:52 | ||
图片预览






文档简介
(共20张PPT)
15.1.1 从分数到分式
学习目标
1.了解分式的概念,能识别分式;在现实情境中进一步理解用字母表示数的意义.
2.会判断分式中的字母满足什么条件时分式有意义,分式值为零.
3.经历从分数到分式概念的形成过程,体会从特殊到一般、从一般到特殊的数学思想方法;通过从具体情境中抽象出数量关系和变化规律,培养学生的符号感.
4.感悟数学在实际生活中的应用,增强数学应用意识,认识到数学的学习价值,激发学习数学的兴趣.
从分数到分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题1:下列各式哪些是整式?
回顾
整式
单个数、单个字母、数与字母的积,字母与字母的积.
几个单项式的和.
单项式
多项式
整式:
不是整式,那么它们是什么呢?
应用新知
巩固新知
课堂小结
布置作业
5÷3=________, 2 ÷ 3=________.
问题3:试用类似分数的形式表示下列两个整式相除:
(1) 90÷x 可以用式子 来表示.
(2) (x+3) ÷(x–6)可以用式子 来表示.
问题2:将下列两个整数相除表示成分数的形式:
创设情境
探究新知
两个整式相除也可以有类似地表示.
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
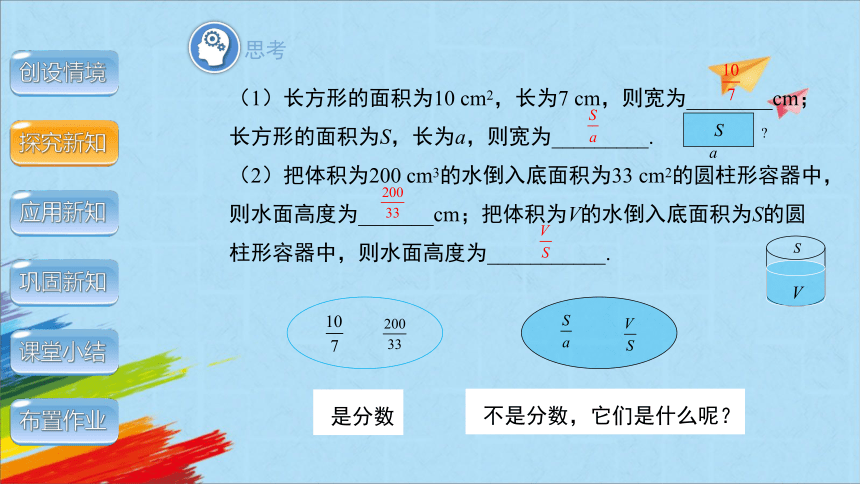
(1)长方形的面积为10 cm2,长为7 cm,则宽为________cm;长方形的面积为S,长为a,则宽为_________.
(2)把体积为200 cm3的水倒入底面积为33 cm2的圆柱形容器中,则水面高度为_______cm;把体积为V的水倒入底面积为S的圆柱形容器中,则水面高度为___________.
思考
是分数
不是分数,它们是什么呢?
S
a
V
S
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
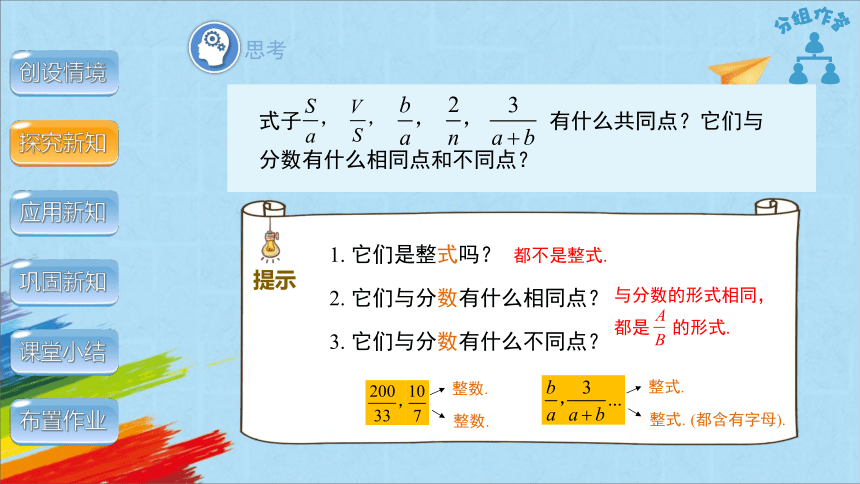
式子 有什么共同点?它们与分数有什么相同点和不同点?
思考
1. 它们是整式吗?
2. 它们与分数有什么相同点?
3. 它们与分数有什么不同点?
都不是整式.
与分数的形式相同,
都是 的形式.
整数.
整数.
整式.
整式.
(都含有字母).
提示
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
一般地,如果A,B表示两个整式,并且B中含有字母,那么式子 叫做分式.A叫做分子,B叫做分母.
1. 分式是不同于整式的另一类式子,两类式子的区别是分母是否含有字母.
2. 分式的分子A可以含有字母,也可以不含字母,分母B中必须含有字母.
3. 由于字母可以表示不同的数,所以分式比分数更具有一般性.
仅表示2÷3的商,而分式 既可以表示2÷3,又可表示(– 5)÷2,8÷(– 9)等.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
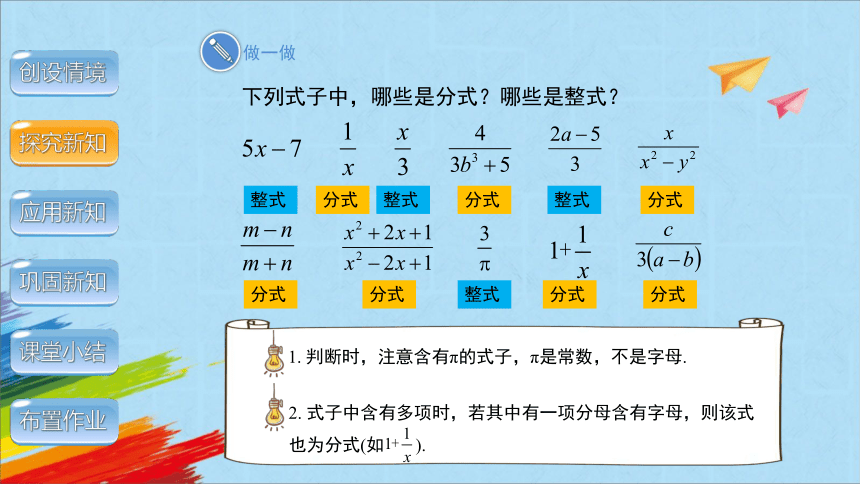
下列式子中,哪些是分式?哪些是整式?
1. 判断时,注意含有π的式子,π是常数,不是字母.
整式
2. 式子中含有多项时,若其中有一项分母含有字母,则该式也为分式(如 ).
整式
整式
整式
分式
分式
分式
分式
分式
分式
分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
提示
1. 分数 有意义吗?
没有意义
分数有意义的条件是分母不为0.
2. 类似地分式 有意义的条件是什么呢?
分式有意义的条件是分母B≠0.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
分式 中,
当分母B=0时, 分式 无意义.
当分母B≠0时,分式 有意义.
(与分子A无关)
当x是什么值时,分式 有意义?
要使分式 有意义,则分母x+3≠0,即x ≠ –3.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
提示
= ( )
在什么条件下,分式 的值为0?
= ( )
时,即A=0
,且B≠0时.
0
0
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
当 =0时,
A=0且B≠0
当x是什么值时,分式 的值是0?
要使分式 的值是0 ,则分子x–1= 0且分母x+3≠0,即x =1.
巩固新知
课堂小结
布置作业
创设情境
下列分式中的字母满足什么条件时分式有意义?
探究新知
应用新知
典型例题
(1)
(2)
(3)
(4)
解:(1)要使分式 有意义,
(2)要使分式 有意义,
(3)要使分式 有意义,
(4)要使分式 有意义,
则分母3x≠0,即x ≠ 0;
则分母x–1≠0,即x ≠ 1;
则分母5–3b≠0,即b ≠ ;
则分母x–y≠0,即x ≠ y.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
下列各式: 其中分式共有( )
A. 1个 B. 2个 C. 3个 D. 4个
B
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
已知分式 ,
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
(3) 当x为何值时,分式的值为零
(2) 分式有意义,即分母 x+2≠0,得 x ≠ –2.
解:
(1) 分式无意义,即分母 x+2=0,得 x= –2.
(3) 分式的值为零,即分母 x+2 ≠0 且分子x2–4=0,
由x+2≠0,可知 x≠–2,
即当x= –2时,分式 无意义.
由x2–4=0,得 x=±2,
综上所述: x=2.
即当x ≠–2时,分式 有意义.
即当x =2时,分式 的值为零.
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习3
无论x为何值,下列分式一定有意义的是( )
A. B. C. D.
D
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习4
在分式 中,如果x= –a,则下列结论中正确的是( )
不论a为何值,分式都无意义.
不论a为何值,分式的值均为零.
若a≠ ,则分式的值是零.
若a≠ ,则分式的值是零.
D
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
从分数到分式
一般地,如果A,B表示两个整式,并且B中含有字母,那么式子 叫做分式.A叫做分子,B叫做分母.
分式 中,
当分母B=0时, 分式 无意义.
当分母B≠0时,分式 有意义.
(与分子A无关)
当A=0且B≠0时,分式 的值为零.
布置作业
教科书第128页,习题1、2 、3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
15.1.1 从分数到分式
学习目标
1.了解分式的概念,能识别分式;在现实情境中进一步理解用字母表示数的意义.
2.会判断分式中的字母满足什么条件时分式有意义,分式值为零.
3.经历从分数到分式概念的形成过程,体会从特殊到一般、从一般到特殊的数学思想方法;通过从具体情境中抽象出数量关系和变化规律,培养学生的符号感.
4.感悟数学在实际生活中的应用,增强数学应用意识,认识到数学的学习价值,激发学习数学的兴趣.
从分数到分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
问题1:下列各式哪些是整式?
回顾
整式
单个数、单个字母、数与字母的积,字母与字母的积.
几个单项式的和.
单项式
多项式
整式:
不是整式,那么它们是什么呢?
应用新知
巩固新知
课堂小结
布置作业
5÷3=________, 2 ÷ 3=________.
问题3:试用类似分数的形式表示下列两个整式相除:
(1) 90÷x 可以用式子 来表示.
(2) (x+3) ÷(x–6)可以用式子 来表示.
问题2:将下列两个整数相除表示成分数的形式:
创设情境
探究新知
两个整式相除也可以有类似地表示.
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
(1)长方形的面积为10 cm2,长为7 cm,则宽为________cm;长方形的面积为S,长为a,则宽为_________.
(2)把体积为200 cm3的水倒入底面积为33 cm2的圆柱形容器中,则水面高度为_______cm;把体积为V的水倒入底面积为S的圆柱形容器中,则水面高度为___________.
思考
是分数
不是分数,它们是什么呢?
S
a
V
S
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
式子 有什么共同点?它们与分数有什么相同点和不同点?
思考
1. 它们是整式吗?
2. 它们与分数有什么相同点?
3. 它们与分数有什么不同点?
都不是整式.
与分数的形式相同,
都是 的形式.
整数.
整数.
整式.
整式.
(都含有字母).
提示
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
一般地,如果A,B表示两个整式,并且B中含有字母,那么式子 叫做分式.A叫做分子,B叫做分母.
1. 分式是不同于整式的另一类式子,两类式子的区别是分母是否含有字母.
2. 分式的分子A可以含有字母,也可以不含字母,分母B中必须含有字母.
3. 由于字母可以表示不同的数,所以分式比分数更具有一般性.
仅表示2÷3的商,而分式 既可以表示2÷3,又可表示(– 5)÷2,8÷(– 9)等.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
做一做
下列式子中,哪些是分式?哪些是整式?
1. 判断时,注意含有π的式子,π是常数,不是字母.
整式
2. 式子中含有多项时,若其中有一项分母含有字母,则该式也为分式(如 ).
整式
整式
整式
分式
分式
分式
分式
分式
分式
分式
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意义,分式中的分母应满足什么条件?
提示
1. 分数 有意义吗?
没有意义
分数有意义的条件是分母不为0.
2. 类似地分式 有意义的条件是什么呢?
分式有意义的条件是分母B≠0.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
分式 中,
当分母B=0时, 分式 无意义.
当分母B≠0时,分式 有意义.
(与分子A无关)
当x是什么值时,分式 有意义?
要使分式 有意义,则分母x+3≠0,即x ≠ –3.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
提示
= ( )
在什么条件下,分式 的值为0?
= ( )
时,即A=0
,且B≠0时.
0
0
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
当 =0时,
A=0且B≠0
当x是什么值时,分式 的值是0?
要使分式 的值是0 ,则分子x–1= 0且分母x+3≠0,即x =1.
巩固新知
课堂小结
布置作业
创设情境
下列分式中的字母满足什么条件时分式有意义?
探究新知
应用新知
典型例题
(1)
(2)
(3)
(4)
解:(1)要使分式 有意义,
(2)要使分式 有意义,
(3)要使分式 有意义,
(4)要使分式 有意义,
则分母3x≠0,即x ≠ 0;
则分母x–1≠0,即x ≠ 1;
则分母5–3b≠0,即b ≠ ;
则分母x–y≠0,即x ≠ y.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
下列各式: 其中分式共有( )
A. 1个 B. 2个 C. 3个 D. 4个
B
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
已知分式 ,
(2) 当x为何值时,分式有意义
(1) 当x为何值时,分式无意义
(3) 当x为何值时,分式的值为零
(2) 分式有意义,即分母 x+2≠0,得 x ≠ –2.
解:
(1) 分式无意义,即分母 x+2=0,得 x= –2.
(3) 分式的值为零,即分母 x+2 ≠0 且分子x2–4=0,
由x+2≠0,可知 x≠–2,
即当x= –2时,分式 无意义.
由x2–4=0,得 x=±2,
综上所述: x=2.
即当x ≠–2时,分式 有意义.
即当x =2时,分式 的值为零.
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习3
无论x为何值,下列分式一定有意义的是( )
A. B. C. D.
D
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习4
在分式 中,如果x= –a,则下列结论中正确的是( )
不论a为何值,分式都无意义.
不论a为何值,分式的值均为零.
若a≠ ,则分式的值是零.
若a≠ ,则分式的值是零.
D
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
从分数到分式
一般地,如果A,B表示两个整式,并且B中含有字母,那么式子 叫做分式.A叫做分子,B叫做分母.
分式 中,
当分母B=0时, 分式 无意义.
当分母B≠0时,分式 有意义.
(与分子A无关)
当A=0且B≠0时,分式 的值为零.
布置作业
教科书第128页,习题1、2 、3.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
