人教版八年级数学上册14.1.4 整式的乘法 第二课时 教学课件 (共18张PPT)
文档属性
| 名称 | 人教版八年级数学上册14.1.4 整式的乘法 第二课时 教学课件 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 16:28:20 | ||
图片预览



文档简介
(共18张PPT)
14.1.4 整式的乘法
第2课时
1.掌握单项式乘多项式的法则,并能运用它进行运算;
2.掌握整式的加、减、乘、乘方等较简单的混合运算,并能灵活运用运算律简化计算;
3.经历探索单项式乘多项式的运算法则的过程,通过类比学习,利用乘法分配律将问题转化,培养学生转化的数学思想;
4.让学生主动参与到探索过程中,培养学生思维的严密性和初步解决问题的能力.
学习目标
单项式乘多项式
思考
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
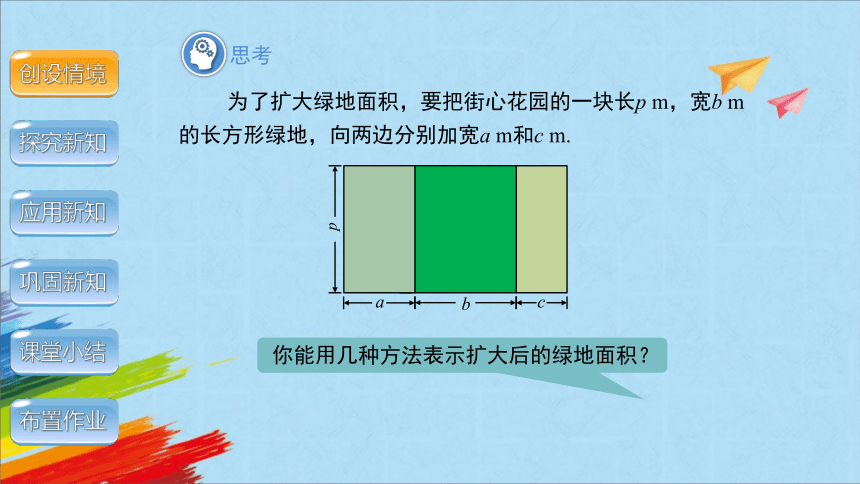
为了扩大绿地面积,要把街心花园的一块长p m,宽b m的长方形绿地,向两边分别加宽a m和c m.
c
b
p
p
a
你能用几种方法表示扩大后的绿地面积?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
b
p
p
a
c
b
p
a
c
p
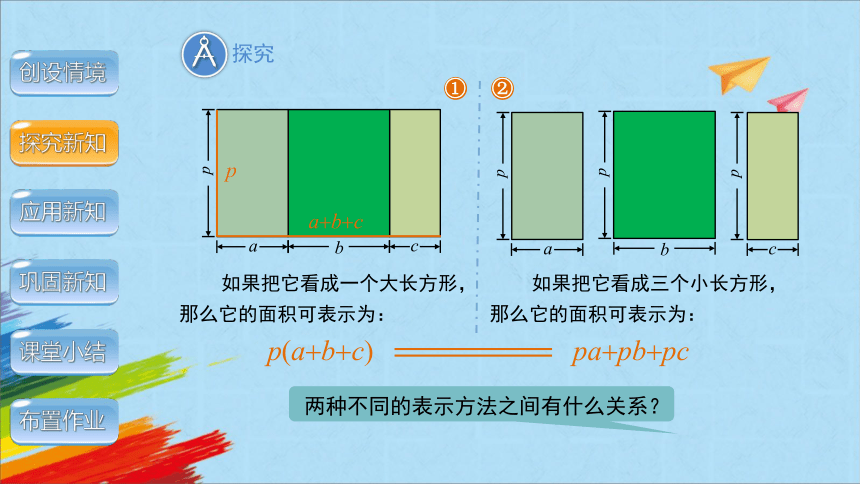
如果把它看成一个大长方形,
那么它的面积可表示为:
a b c
p
p(a b c)
如果把它看成三个小长方形,
那么它的面积可表示为:
pa pb pc
①
②
两种不同的表示方法之间有什么关系?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
你还能通过别的方法得到等式p(a b c) pa pb pc吗?
p(a b c)
pa
pb
pc
类比单项式乘单项式,说说这是什么运算?
乘法分配律
单项式乘多项式
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
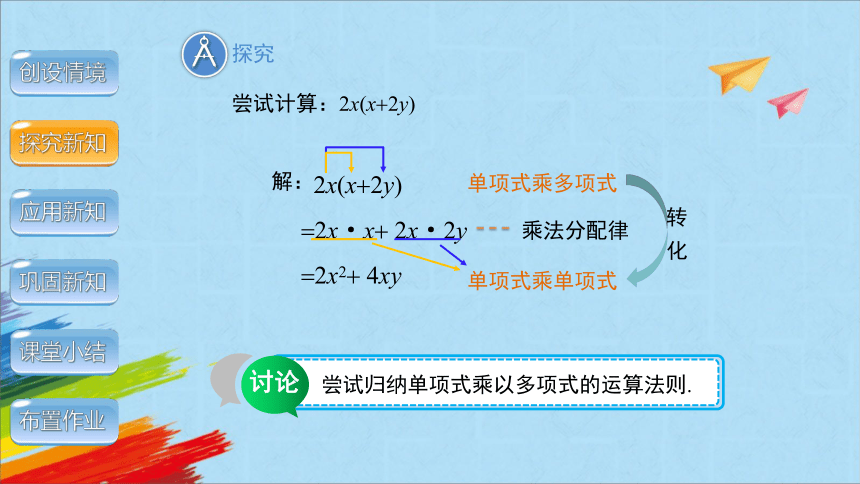
尝试计算:2x(x 2y)
2x(x 2y)
2x·x 2x·2y
2x2 4xy
乘法分配律
单项式乘单项式
讨论
尝试归纳单项式乘以多项式的运算法则.
单项式乘多项式
解:
转化
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
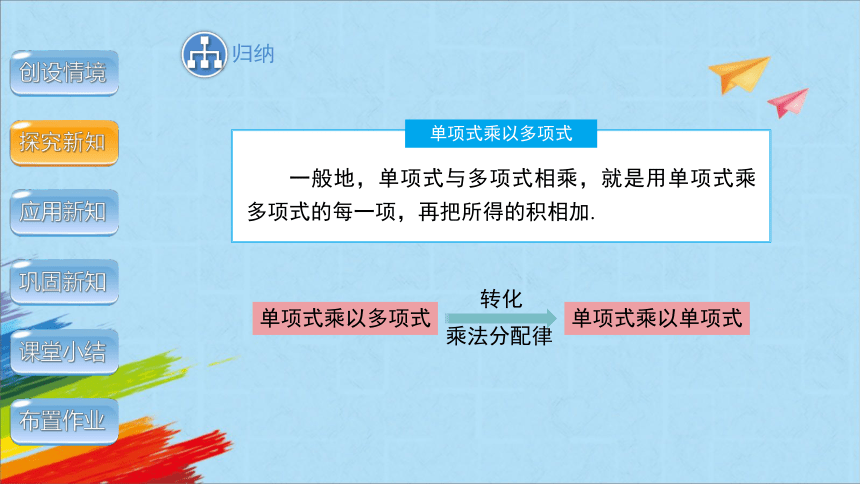
单项式乘以多项式
一般地,单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.
归纳
单项式乘以多项式
单项式乘以单项式
转化
乘法分配律
解:(1) 原式 ( 4x2)·(3x) ( 4x2) 1
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1 计算:
(1) ( 4x2)(3x 1); (2) .
(2) 原式
( 4x2)·(3x) 4x2 1
1.底数不变;
2.指数相加.
1.非零单项式乘多项式,结果是一个多项式.
2.结果的项数与所乘多项式的项数相等;
3.正确确定积的符号:多项式的每一项包括前面的符号,要注意积的各项符号的确定,同号相乘得正,异号相乘得负.
12x3 4x2
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
做一做
1.计算:
(1) 3a(5a 2b); (2) (x 3y)( 6x)
解:(1) 3a(5a 2b)
3a·5a 3a·2b
15a2 6ab
异号得负
同号得正
(2) (x 3y)( 6x)
x·6x 3y·6x
6x2 18xy
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
做一做
2.判断下面的计算是否正确,如果不对,请改正.
(1) (x 2y)( 2x) 2x2 4xy
(2)
(3) 4xy(3x2 2xy 1) 12x3y 8x2y2
(x 2y)( 2x) 2x2 4xy
4xy(3x2 2xy 1) 12x3y 8x2y2 4xy
1.底数不变;
2.指数相加.
1.注意符号;
2.不要漏乘,尤其是“1, 1”.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2 先化简,再求值:3a(4a2 4a 3) (2a)2(3a 2),
其中a 2.
解:原式 3a(4a2 4a 3) 4a2(3a 2)
12a3 12a2 9a 12a3 8a2
20a2 9a.
当a 2时,
原式 20 4 9 2 98.
.
先算乘方,再算单项式乘多项式.
【选讲】
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例3 如果( 3x)2(x2 2nx 2)的展开式中不含x3项,求n的值.
解:( 3x)2(x2 2nx 2)
9x2(x2 2nx 2)
9x4 18nx3 18x2.
∵展开式中不含x3项,
∴n 0.
.
多项式中不含哪一项,则表示这一项的系数为0.
【选讲】
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
1.填空:
(1) 5(m n 5) .
(2) ( 2a 3b)( 4ab) .
(3) 2x( 4x2 6x 8) .
(4) (a 2b)( c) .
抢答
5m 5n 25
8a2b 12ab2
8x3 12x2 16x
ac 2bc
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
2.若m x2 2y2,n 2x2 y2 1,那么2m 4n化简后为( )
A. 6x2 8y2 4 B. 10x2 8y2 4
C. 6x2 8y2 4 D. 10x2 8y2 4
解:2m 4n 2(x2 2y2) 4(2x2 y2 1)
2x2 4y2 8x2 4y2 4
6x2 8y2 4
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
3.计算:
(1) am(am a2 7) (2) ( 2x2y)2(xy2 x2y x2)
解:(1)原式 am·am am·a2 7am
a2m am 2 7am
(2)原式 4x4y2(xy2 x2y x2)
4x4y2·xy2 4x4y2·x2y 4x4y2·x2
4x5y4 4x6y3 4x6y2
带 的为选做题
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
注意事项:
①单项式与多项式中的项勿漏乘,尤其是1或 1;
②注意符号:多项式的每一项都包括前面的符号,还要注意单项式的符号,从而正确确定积的符号;
③注意运算顺序:有乘方先算乘方,再算单项式乘多项式;
④多项式中不含哪一项,则表示这一项的系数为0.
单项式乘多项式
运算法则:
单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.
带 的为选讲内容
布置作业
教科书第100页练习题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
14.1.4 整式的乘法
第2课时
1.掌握单项式乘多项式的法则,并能运用它进行运算;
2.掌握整式的加、减、乘、乘方等较简单的混合运算,并能灵活运用运算律简化计算;
3.经历探索单项式乘多项式的运算法则的过程,通过类比学习,利用乘法分配律将问题转化,培养学生转化的数学思想;
4.让学生主动参与到探索过程中,培养学生思维的严密性和初步解决问题的能力.
学习目标
单项式乘多项式
思考
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
为了扩大绿地面积,要把街心花园的一块长p m,宽b m的长方形绿地,向两边分别加宽a m和c m.
c
b
p
p
a
你能用几种方法表示扩大后的绿地面积?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
b
p
p
a
c
b
p
a
c
p
如果把它看成一个大长方形,
那么它的面积可表示为:
a b c
p
p(a b c)
如果把它看成三个小长方形,
那么它的面积可表示为:
pa pb pc
①
②
两种不同的表示方法之间有什么关系?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
你还能通过别的方法得到等式p(a b c) pa pb pc吗?
p(a b c)
pa
pb
pc
类比单项式乘单项式,说说这是什么运算?
乘法分配律
单项式乘多项式
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
尝试计算:2x(x 2y)
2x(x 2y)
2x·x 2x·2y
2x2 4xy
乘法分配律
单项式乘单项式
讨论
尝试归纳单项式乘以多项式的运算法则.
单项式乘多项式
解:
转化
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
单项式乘以多项式
一般地,单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.
归纳
单项式乘以多项式
单项式乘以单项式
转化
乘法分配律
解:(1) 原式 ( 4x2)·(3x) ( 4x2) 1
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1 计算:
(1) ( 4x2)(3x 1); (2) .
(2) 原式
( 4x2)·(3x) 4x2 1
1.底数不变;
2.指数相加.
1.非零单项式乘多项式,结果是一个多项式.
2.结果的项数与所乘多项式的项数相等;
3.正确确定积的符号:多项式的每一项包括前面的符号,要注意积的各项符号的确定,同号相乘得正,异号相乘得负.
12x3 4x2
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
做一做
1.计算:
(1) 3a(5a 2b); (2) (x 3y)( 6x)
解:(1) 3a(5a 2b)
3a·5a 3a·2b
15a2 6ab
异号得负
同号得正
(2) (x 3y)( 6x)
x·6x 3y·6x
6x2 18xy
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
做一做
2.判断下面的计算是否正确,如果不对,请改正.
(1) (x 2y)( 2x) 2x2 4xy
(2)
(3) 4xy(3x2 2xy 1) 12x3y 8x2y2
(x 2y)( 2x) 2x2 4xy
4xy(3x2 2xy 1) 12x3y 8x2y2 4xy
1.底数不变;
2.指数相加.
1.注意符号;
2.不要漏乘,尤其是“1, 1”.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2 先化简,再求值:3a(4a2 4a 3) (2a)2(3a 2),
其中a 2.
解:原式 3a(4a2 4a 3) 4a2(3a 2)
12a3 12a2 9a 12a3 8a2
20a2 9a.
当a 2时,
原式 20 4 9 2 98.
.
先算乘方,再算单项式乘多项式.
【选讲】
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
典型例题
例3 如果( 3x)2(x2 2nx 2)的展开式中不含x3项,求n的值.
解:( 3x)2(x2 2nx 2)
9x2(x2 2nx 2)
9x4 18nx3 18x2.
∵展开式中不含x3项,
∴n 0.
.
多项式中不含哪一项,则表示这一项的系数为0.
【选讲】
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
1.填空:
(1) 5(m n 5) .
(2) ( 2a 3b)( 4ab) .
(3) 2x( 4x2 6x 8) .
(4) (a 2b)( c) .
抢答
5m 5n 25
8a2b 12ab2
8x3 12x2 16x
ac 2bc
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
2.若m x2 2y2,n 2x2 y2 1,那么2m 4n化简后为( )
A. 6x2 8y2 4 B. 10x2 8y2 4
C. 6x2 8y2 4 D. 10x2 8y2 4
解:2m 4n 2(x2 2y2) 4(2x2 y2 1)
2x2 4y2 8x2 4y2 4
6x2 8y2 4
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
3.计算:
(1) am(am a2 7) (2) ( 2x2y)2(xy2 x2y x2)
解:(1)原式 am·am am·a2 7am
a2m am 2 7am
(2)原式 4x4y2(xy2 x2y x2)
4x4y2·xy2 4x4y2·x2y 4x4y2·x2
4x5y4 4x6y3 4x6y2
带 的为选做题
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
注意事项:
①单项式与多项式中的项勿漏乘,尤其是1或 1;
②注意符号:多项式的每一项都包括前面的符号,还要注意单项式的符号,从而正确确定积的符号;
③注意运算顺序:有乘方先算乘方,再算单项式乘多项式;
④多项式中不含哪一项,则表示这一项的系数为0.
单项式乘多项式
运算法则:
单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.
带 的为选讲内容
布置作业
教科书第100页练习题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
