人教版八年级数学上册15.1.2《分式的基本性质》第1课时 教学课件(共17张PPT)
文档属性
| 名称 | 人教版八年级数学上册15.1.2《分式的基本性质》第1课时 教学课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 15:27:19 | ||
图片预览






文档简介
(共17张PPT)
15.1.2 分式的基本性质
第1课时
学习目标
1.理解分式的基本性质.
2.能够运用分式的基本性质进行分式的变形.
3.通过类比分数的基本性质,探索分式的基本性质,初步掌握类比的思想方法.
4.通过研究解决问题的过程,培养学生合作交流意识与探究精神.
分式的基本性质
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
分数的基本性质是什么?
一个分数的分子、分母乘(或除以)同一个不为0的数,分数的值不变.
如果c≠0,
=
=
一般地,对于任意一个分数 ,有 、
(c≠0) ,其中a,b,c是数.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
思考
俩人一组
合作完成
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.
分式的基本性质
归纳
(C≠0),
其中A,B,C是整式.
式子表示
1. 分子,分母同乘(除以)同一个数.
2.乘(除以)对象为非零整式.
巩固新知
课堂小结
布置作业
创设情境
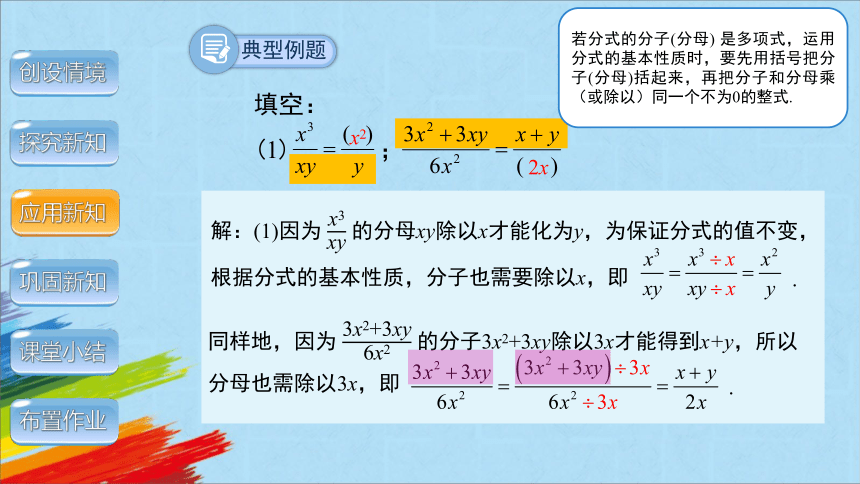
根据分式的基本性质,我们可以进行分式的恒等变形.
填空:
(1) ;
解:(1)因为 的分母xy除以x才能化为y,为保证分式的值不变,根据分式的基本性质,分子也需要除以x,即
.
看分母如何变化,想分子如何变化.
同样地,因为 的分子3x2+3xy除以3x才能得到x+y,所以分母也需除以3x,即
.
看分子如何变化,想分母如何变化.
探究新知
应用新知
若分式的分子(分母) 是多项式,运用分式的基本性质时,要先用括号把分子(分母)括起来,再把分子和分母乘(或除以)同一个不为0的整式.
典型例题
巩固新知
课堂小结
布置作业
创设情境
填空:
(2) ;
解:(2)因为 的分母ab乘a才能化为a2b,为保证分式的值不变,根据分式的基本性质,分子也需要乘a,即
.
同样地,因为的分母a2乘b才能化为a2b ,所以分子也需乘b,即
看分母如何变化,想分子如何变化.
=.
探究新知
应用新知
典型例题
课堂小结
布置作业
创设情境
填空:
(1)
(2)
(3)
(4)
分析:解决分式的恒等变形有关的题目,一般从分子或分母的已知部分入手,先观察等号两边的分子(或分母)发生了怎样的变化,再通过对分母(或分子)作相同的变形求解.
探究新知
应用新知
巩固新知
练习1
随堂练习
课堂小结
布置作业
创设情境
(2)
(3)
(4)
探究新知
(1)
分母乘以a
分子乘以a
分母除以x
分子除以x
分母乘以(x+y)
分子乘以(x+y)
分母乘以(m-n)
分子乘以(m-n)
应用新知
巩固新知
随堂练习
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
D
减2
加2
乘2
分子除以a,分母除以b
若a≠b,则下列分式化简正确的是( )
A.
B.
C.
D.
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
不改变分式的值,使下列分式的分子分母都不含“– ”号.
(1) ; (2) ; (3) .
解:(1)
(2)
(3)
应用新知
课堂小结
布置作业
创设情境
探究新知
巩固新知
归纳
分式的分子、分母与分式本身这三处的正负号,同时改变两处,分式的值不变.
分式的符号法则
式子表示:
,
当分式的分子、分母是多项式时,不要把分子或分母第一项的符号误认为是分子或分母的符号.
应用新知
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习4
分析:先按照题目的要求计算出变化后的分式,然后与原分式进行比较,看结果是否等于原来的分式即可解答.
若x,y的值均扩大为原来的3倍,则下列分式的值保持不变的是( )
A. B. C. D.
课堂小结
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
D
若x,y的值均扩大为原来的3倍,则下列分式的值保持不变的是( )
A. B. C. D.
练习4
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式的基本性质
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.
分式的基本性质
(C≠0),其中A,B,C是整式.
分式的分子、分母与分式本身这三处的正负号,同时改变两处,分式的值不变.
用式子表示:
或
分式的符号法则
布置作业
教科书第133页习题15.1
1题、4题 、5题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
15.1.2 分式的基本性质
第1课时
学习目标
1.理解分式的基本性质.
2.能够运用分式的基本性质进行分式的变形.
3.通过类比分数的基本性质,探索分式的基本性质,初步掌握类比的思想方法.
4.通过研究解决问题的过程,培养学生合作交流意识与探究精神.
分式的基本性质
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
回顾
分数的基本性质是什么?
一个分数的分子、分母乘(或除以)同一个不为0的数,分数的值不变.
如果c≠0,
=
=
一般地,对于任意一个分数 ,有 、
(c≠0) ,其中a,b,c是数.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
类比分数的基本性质,你能猜想分式有什么性质吗?
思考
俩人一组
合作完成
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.
分式的基本性质
归纳
(C≠0),
其中A,B,C是整式.
式子表示
1. 分子,分母同乘(除以)同一个数.
2.乘(除以)对象为非零整式.
巩固新知
课堂小结
布置作业
创设情境
根据分式的基本性质,我们可以进行分式的恒等变形.
填空:
(1) ;
解:(1)因为 的分母xy除以x才能化为y,为保证分式的值不变,根据分式的基本性质,分子也需要除以x,即
.
看分母如何变化,想分子如何变化.
同样地,因为 的分子3x2+3xy除以3x才能得到x+y,所以分母也需除以3x,即
.
看分子如何变化,想分母如何变化.
探究新知
应用新知
若分式的分子(分母) 是多项式,运用分式的基本性质时,要先用括号把分子(分母)括起来,再把分子和分母乘(或除以)同一个不为0的整式.
典型例题
巩固新知
课堂小结
布置作业
创设情境
填空:
(2) ;
解:(2)因为 的分母ab乘a才能化为a2b,为保证分式的值不变,根据分式的基本性质,分子也需要乘a,即
.
同样地,因为的分母a2乘b才能化为a2b ,所以分子也需乘b,即
看分母如何变化,想分子如何变化.
=.
探究新知
应用新知
典型例题
课堂小结
布置作业
创设情境
填空:
(1)
(2)
(3)
(4)
分析:解决分式的恒等变形有关的题目,一般从分子或分母的已知部分入手,先观察等号两边的分子(或分母)发生了怎样的变化,再通过对分母(或分子)作相同的变形求解.
探究新知
应用新知
巩固新知
练习1
随堂练习
课堂小结
布置作业
创设情境
(2)
(3)
(4)
探究新知
(1)
分母乘以a
分子乘以a
分母除以x
分子除以x
分母乘以(x+y)
分子乘以(x+y)
分母乘以(m-n)
分子乘以(m-n)
应用新知
巩固新知
随堂练习
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
D
减2
加2
乘2
分子除以a,分母除以b
若a≠b,则下列分式化简正确的是( )
A.
B.
C.
D.
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
不改变分式的值,使下列分式的分子分母都不含“– ”号.
(1) ; (2) ; (3) .
解:(1)
(2)
(3)
应用新知
课堂小结
布置作业
创设情境
探究新知
巩固新知
归纳
分式的分子、分母与分式本身这三处的正负号,同时改变两处,分式的值不变.
分式的符号法则
式子表示:
,
当分式的分子、分母是多项式时,不要把分子或分母第一项的符号误认为是分子或分母的符号.
应用新知
布置作业
创设情境
随堂练习
探究新知
巩固新知
练习4
分析:先按照题目的要求计算出变化后的分式,然后与原分式进行比较,看结果是否等于原来的分式即可解答.
若x,y的值均扩大为原来的3倍,则下列分式的值保持不变的是( )
A. B. C. D.
课堂小结
应用新知
课堂小结
布置作业
创设情境
随堂练习
探究新知
巩固新知
D
若x,y的值均扩大为原来的3倍,则下列分式的值保持不变的是( )
A. B. C. D.
练习4
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式的基本性质
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.
分式的基本性质
(C≠0),其中A,B,C是整式.
分式的分子、分母与分式本身这三处的正负号,同时改变两处,分式的值不变.
用式子表示:
或
分式的符号法则
布置作业
教科书第133页习题15.1
1题、4题 、5题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
