人教版八年级数学上册15.3《分式方程》第2课时 教学课件(共17张PPT)
文档属性
| 名称 | 人教版八年级数学上册15.3《分式方程》第2课时 教学课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 15:32:00 | ||
图片预览






文档简介
(共17张PPT)
15.3 分式方程
第2课时
学习目标
1.会列分式方程解决实际问题;
2.能根据题意找出正确的等量关系,列出分式方程并求解,会根据实际意义验证结果是否合理;
3.通过分式方程的应用学习,培养学生的数学应用意识,提高分析问题解决问题的能力;
4.通过解决实际问题,使学生感受到数学知识能够解决生活中的问题,提升学生对数学的热爱.
分式方程的应用
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
一艘轮船在静水中的最大航速为30 km/h,它以最大航速沿江顺流航行90 km所用的时间,与以最大航速逆流航行60 km所用的时间相等,则江水的流速为多少?
V顺水= V船速+ V水速
V逆水= V船速 – V水速
S= v·t
路程= 速度·时间
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
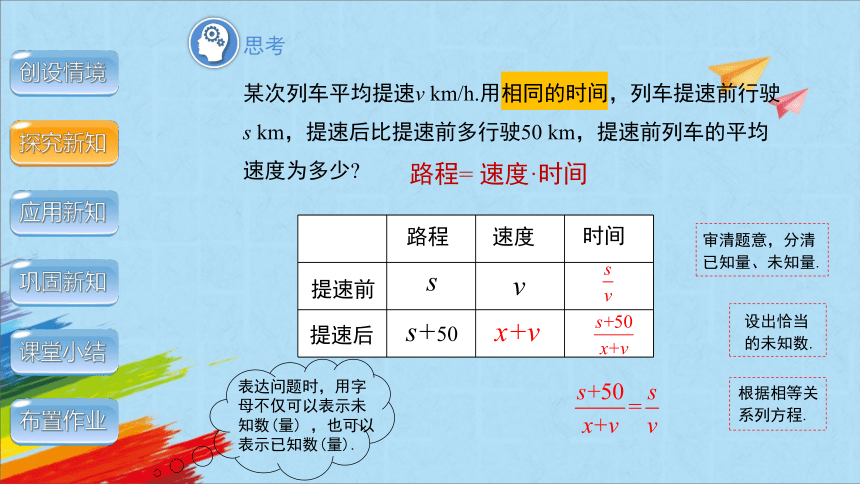
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少
思考
路程= 速度·时间
提速前
提速后
路程
速度
时间
s
s+50
x+v
v
审清题意,分清已知量、未知量.
设出恰当的未知数.
根据相等关系列方程.
表达问题时,用字母不仅可以表示未知数(量) ,也可以表示已知数(量).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少
思考
解方程.
解:设提速前这次列车的平均速度为x km/h,则提速前它行驶s km所用时间为 h;提速后列车的平均速度为(x+v)km/h,提速后它行驶(s+50)km所用时间为 h.
根据行驶时间的等量关系,得
方程两边乘x(x+v),得
s(x+v)=x(s+50)
解得:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少
思考
检验.
答.
检验:由v,s都是正数,得 时,x(x+v)≠0.
所以,原分式方程的解为
答:提速前列车的平均速度为 km/h.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
审:审清题意,找出题中的相等关系,分清题中的已知量、未知量;
设:设出恰当的未知数,注意单位和语言的完整性;
列:根据题中的相等关系,正确列出分式方程;
解:解所列分式方程;
验:既要检验所得的解是否为所列分式方程的解,又要检验所得的
解是否符合实际问题的要求;
答:写出答案.
列分式方程解决实际问题的一般步骤
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
分析:甲队1个月完成总工程的 ,设乙队单独施工一个月能完成总工程的 ,那么甲队半个月完成总工程的___,乙队半个月完成总工程的____,两队半个月完成总工程的_____.
工程问题:工作总量=工作效率×工作时间
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
甲队施工1个月的工程量+甲队施工半个月的工程量+乙队施工半个月的工程量=总工程量(记为1).
找相等关系.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
解:设乙队单独施工1个月能完成总工程的 ,记总工程量为1,
根据工程的实际进度,得 .
方程两边同时乘以6x,得2x+x+3=6x.解得x=1.
检验:当x=1时,6x≠0.
所以原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队的施工速度快.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
施工队要铺设1000米的管道,因在中考期间需停工2天,每天要比原计划多施工30米才能按时完成任务.设原计划每天施工x米,所列方程正确的是( )
A.
B.
C.
D.
A
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
甲、乙二人做某种机械零件,已知每小时甲比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,设乙每小时做x个零件,以下所列方程正确的是( )
A.
B.
C.
D.
C
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
某市区一条主要街道的改造工程有甲、乙两个工程队投标,经测算,若由两个工程队共同工作,则恰好12天能够完成任务;若两个工程队共同工作9天后,剩下的任务由甲工程队单独完成,则还需5天.现要从这两个工程队中选出一个工程队单独完成,从缩短工期的角度考虑,你认为应该选择哪个工程队?
分析:
“甲、乙两个工程队共同工作9天的工作量+甲工程队单独工作5天的工作量=总工作量(记为1)”.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
解:设甲工程队单独完成工程需要x天.
方程两边同时乘以x ,得 ,解得 x=20.
根据题意,得 .
经检验:x=20是原分式方程的解.
因为 ,所以乙工程队单独完成工程需要30天.
因为20<30,所以选择甲队.
答:从缩短工期的角度考虑,应该选择甲工程队.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式方程的应用
审:审清题意,找出题中的相等关系,分清题中的已知量、未知量;
设:设出恰当的未知数,注意单位和语言的完整性;
列:根据题中的相等关系,正确列出分式方程;
解:解所列分式方程;
验:既要检验所得的解是否为所列分式方程的解,又要检验所得的解是否符合实际问题的要求;
答:写出答案.
列分式方程解决实际问题的一般步骤
布置作业
教科书第154页练习1、2.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
15.3 分式方程
第2课时
学习目标
1.会列分式方程解决实际问题;
2.能根据题意找出正确的等量关系,列出分式方程并求解,会根据实际意义验证结果是否合理;
3.通过分式方程的应用学习,培养学生的数学应用意识,提高分析问题解决问题的能力;
4.通过解决实际问题,使学生感受到数学知识能够解决生活中的问题,提升学生对数学的热爱.
分式方程的应用
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
一艘轮船在静水中的最大航速为30 km/h,它以最大航速沿江顺流航行90 km所用的时间,与以最大航速逆流航行60 km所用的时间相等,则江水的流速为多少?
V顺水= V船速+ V水速
V逆水= V船速 – V水速
S= v·t
路程= 速度·时间
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少
思考
路程= 速度·时间
提速前
提速后
路程
速度
时间
s
s+50
x+v
v
审清题意,分清已知量、未知量.
设出恰当的未知数.
根据相等关系列方程.
表达问题时,用字母不仅可以表示未知数(量) ,也可以表示已知数(量).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少
思考
解方程.
解:设提速前这次列车的平均速度为x km/h,则提速前它行驶s km所用时间为 h;提速后列车的平均速度为(x+v)km/h,提速后它行驶(s+50)km所用时间为 h.
根据行驶时间的等量关系,得
方程两边乘x(x+v),得
s(x+v)=x(s+50)
解得:
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少
思考
检验.
答.
检验:由v,s都是正数,得 时,x(x+v)≠0.
所以,原分式方程的解为
答:提速前列车的平均速度为 km/h.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
审:审清题意,找出题中的相等关系,分清题中的已知量、未知量;
设:设出恰当的未知数,注意单位和语言的完整性;
列:根据题中的相等关系,正确列出分式方程;
解:解所列分式方程;
验:既要检验所得的解是否为所列分式方程的解,又要检验所得的
解是否符合实际问题的要求;
答:写出答案.
列分式方程解决实际问题的一般步骤
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
分析:甲队1个月完成总工程的 ,设乙队单独施工一个月能完成总工程的 ,那么甲队半个月完成总工程的___,乙队半个月完成总工程的____,两队半个月完成总工程的_____.
工程问题:工作总量=工作效率×工作时间
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
甲队施工1个月的工程量+甲队施工半个月的工程量+乙队施工半个月的工程量=总工程量(记为1).
找相等关系.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
解:设乙队单独施工1个月能完成总工程的 ,记总工程量为1,
根据工程的实际进度,得 .
方程两边同时乘以6x,得2x+x+3=6x.解得x=1.
检验:当x=1时,6x≠0.
所以原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队的施工速度快.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
施工队要铺设1000米的管道,因在中考期间需停工2天,每天要比原计划多施工30米才能按时完成任务.设原计划每天施工x米,所列方程正确的是( )
A.
B.
C.
D.
A
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
甲、乙二人做某种机械零件,已知每小时甲比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等,设乙每小时做x个零件,以下所列方程正确的是( )
A.
B.
C.
D.
C
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
某市区一条主要街道的改造工程有甲、乙两个工程队投标,经测算,若由两个工程队共同工作,则恰好12天能够完成任务;若两个工程队共同工作9天后,剩下的任务由甲工程队单独完成,则还需5天.现要从这两个工程队中选出一个工程队单独完成,从缩短工期的角度考虑,你认为应该选择哪个工程队?
分析:
“甲、乙两个工程队共同工作9天的工作量+甲工程队单独工作5天的工作量=总工作量(记为1)”.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
解:设甲工程队单独完成工程需要x天.
方程两边同时乘以x ,得 ,解得 x=20.
根据题意,得 .
经检验:x=20是原分式方程的解.
因为 ,所以乙工程队单独完成工程需要30天.
因为20<30,所以选择甲队.
答:从缩短工期的角度考虑,应该选择甲工程队.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
分式方程的应用
审:审清题意,找出题中的相等关系,分清题中的已知量、未知量;
设:设出恰当的未知数,注意单位和语言的完整性;
列:根据题中的相等关系,正确列出分式方程;
解:解所列分式方程;
验:既要检验所得的解是否为所列分式方程的解,又要检验所得的解是否符合实际问题的要求;
答:写出答案.
列分式方程解决实际问题的一般步骤
布置作业
教科书第154页练习1、2.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
