人教版八年级数学上册14.3.2公式法 第1课时 教学课件(共15张PPT)
文档属性
| 名称 | 人教版八年级数学上册14.3.2公式法 第1课时 教学课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 16:55:22 | ||
图片预览






文档简介
(共15张PPT)
14.3.2 公式法
第1课时
学习目标
1. 能够理解并熟练运用平方差公式分解因式,体会转化思想;
重点
公式法
难点
3. 能够综合运用提公因式法、平方差公式法分解因式;
2.理解并探索平方差公式的几何意义;
4. 培养学生灵活运用公式,勇于探索科学规律的意识.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察思考
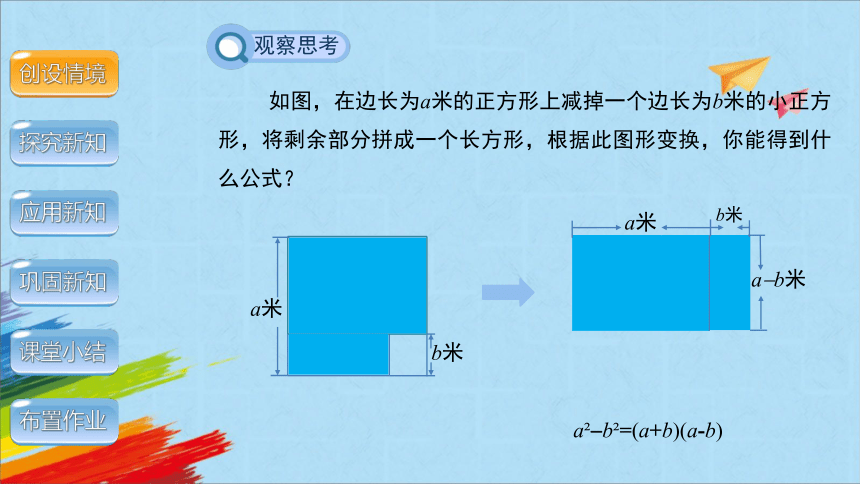
如图,在边长为a米的正方形上减掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a b =(a+b)(a-b)
a米
b米
a米
b米
a b米
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
多项式a -b 有什么特点?你能将它分解因式吗?依据是什么?
这个多项式是两个数的平方差的形式
a b =(a+b)(a-b)
两个数的平方差,等于这两个数的和与这两个数的差的积
(a+b)(a-b)=a b
整式的乘法
因式分解
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
做一做
1 x y
下列多项式能否用平方差公式因式分解?为什么?
2 x y
3 x y
4 x y
这是两数平方和;
x y =(x+y)(x y);
x y =(y+x)(y x);
这是两数平方和的相反数.
判断依据:1.各项能否写成平方项2.确定两数平方是否相减
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
1 4x 9
典型例题
例1 分解因式:
1 原式 2x 3
2x+3 2x 3
2 x+p x+q
分析:
(2) x+p x+q =
x+p + x+q
x+p x+q
注意:公式a b (a + b)(a b)中的a,b可以表示数、单项式、多项式.
2x+p+q p q
a b (a + b)(a b)
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
做一做
(1)(a+b) 4a
(2)9(m+n) (m n)
解:(1)原式= a+b+2a a+b 2a
= 3a+b b a
(2)原式= 3m+3n m+n 3m+3n m n
= 2m+4n 4m+2n
=4 m+2n 2m+n
若用平方差公式分解后的结果中有公因式,一定要再用提公因式法继续分解.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
1 x4 y4
典型例题
2 a b ab
例2 分解因式:
= x y x y
ab a+1 a 1
x y x y x y
ab a 1
(1)原式=
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解,直到不能分解为止.
分解因式时,一般有公因式先用提公因式法进行分解,然后再用公式法最后进行检查.
(x ) (y )
(2)原式
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
做一做
=5m (a4 b4)
=5m a2+b2 a2 b2
= 5m a2+b2 a+b (a b)
(2)原式=a 4b a+2b
= a+2b a 2b a+2b
= a+2b a 2b 1
(1)5m a4 5m b4
2 a 4b a 2b
解: (1)原式
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
拓展
例3 计算下列各题:
(1)101 99
(2)53.5 ×4 46.5 ×4
解:(1)原式=(101+99) (101 99)
=400
(2)原式=4 (53.5 46.5 )
=4× (53.5+46.5)×(53.5 46.5)
=4×100×7
=2800
方法总结:较为复杂的有理数运算,可以运用因式分解对其进行变形,使运算得以简化.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
拓展
例4 已知x y = 2,x+y 1,求x y,x,y的值
解:∵ x y =(x+y)(x y) 2,
x+y 1①,
∴ x y 2②
联立①②组成二元一次方程组,
解得:
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.多项式4a a 分解因式的结果是
A.a(4 a ) B. a(2 a)(2+a) C. a(a 2)(a+2) D. a(2 a)
1.把下列各式分解因式:
(1)16a 9b =______________
4a+3b 4a 3b
(2)(a+b) (a b) =_______
4ab
(3)2x 8=__________
2(x+2)(x 2)
(4) a4+16=______________
(4+a )(2+a)(2 a)
B
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
1. 提取公因式
平方差公式:
公式法
解题一般步骤:
2.套用平方差公式解题
a b =(a+b)(a-b)
注意事项:
多项式的因式分解是否分解到不能再分解为止.
布置作业
教科书第117页练习第2题
14.3第2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
14.3.2 公式法
第1课时
学习目标
1. 能够理解并熟练运用平方差公式分解因式,体会转化思想;
重点
公式法
难点
3. 能够综合运用提公因式法、平方差公式法分解因式;
2.理解并探索平方差公式的几何意义;
4. 培养学生灵活运用公式,勇于探索科学规律的意识.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察思考
如图,在边长为a米的正方形上减掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a b =(a+b)(a-b)
a米
b米
a米
b米
a b米
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
想一想
多项式a -b 有什么特点?你能将它分解因式吗?依据是什么?
这个多项式是两个数的平方差的形式
a b =(a+b)(a-b)
两个数的平方差,等于这两个数的和与这两个数的差的积
(a+b)(a-b)=a b
整式的乘法
因式分解
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
做一做
1 x y
下列多项式能否用平方差公式因式分解?为什么?
2 x y
3 x y
4 x y
这是两数平方和;
x y =(x+y)(x y);
x y =(y+x)(y x);
这是两数平方和的相反数.
判断依据:1.各项能否写成平方项2.确定两数平方是否相减
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
1 4x 9
典型例题
例1 分解因式:
1 原式 2x 3
2x+3 2x 3
2 x+p x+q
分析:
(2) x+p x+q =
x+p + x+q
x+p x+q
注意:公式a b (a + b)(a b)中的a,b可以表示数、单项式、多项式.
2x+p+q p q
a b (a + b)(a b)
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
做一做
(1)(a+b) 4a
(2)9(m+n) (m n)
解:(1)原式= a+b+2a a+b 2a
= 3a+b b a
(2)原式= 3m+3n m+n 3m+3n m n
= 2m+4n 4m+2n
=4 m+2n 2m+n
若用平方差公式分解后的结果中有公因式,一定要再用提公因式法继续分解.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
1 x4 y4
典型例题
2 a b ab
例2 分解因式:
= x y x y
ab a+1 a 1
x y x y x y
ab a 1
(1)原式=
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解,直到不能分解为止.
分解因式时,一般有公因式先用提公因式法进行分解,然后再用公式法最后进行检查.
(x ) (y )
(2)原式
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
做一做
=5m (a4 b4)
=5m a2+b2 a2 b2
= 5m a2+b2 a+b (a b)
(2)原式=a 4b a+2b
= a+2b a 2b a+2b
= a+2b a 2b 1
(1)5m a4 5m b4
2 a 4b a 2b
解: (1)原式
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
拓展
例3 计算下列各题:
(1)101 99
(2)53.5 ×4 46.5 ×4
解:(1)原式=(101+99) (101 99)
=400
(2)原式=4 (53.5 46.5 )
=4× (53.5+46.5)×(53.5 46.5)
=4×100×7
=2800
方法总结:较为复杂的有理数运算,可以运用因式分解对其进行变形,使运算得以简化.
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
拓展
例4 已知x y = 2,x+y 1,求x y,x,y的值
解:∵ x y =(x+y)(x y) 2,
x+y 1①,
∴ x y 2②
联立①②组成二元一次方程组,
解得:
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.多项式4a a 分解因式的结果是
A.a(4 a ) B. a(2 a)(2+a) C. a(a 2)(a+2) D. a(2 a)
1.把下列各式分解因式:
(1)16a 9b =______________
4a+3b 4a 3b
(2)(a+b) (a b) =_______
4ab
(3)2x 8=__________
2(x+2)(x 2)
(4) a4+16=______________
(4+a )(2+a)(2 a)
B
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
1. 提取公因式
平方差公式:
公式法
解题一般步骤:
2.套用平方差公式解题
a b =(a+b)(a-b)
注意事项:
多项式的因式分解是否分解到不能再分解为止.
布置作业
教科书第117页练习第2题
14.3第2题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
