人教版八年级数学上册 12.3角的平分线的性质 教学课件(共20张PPT))
文档属性
| 名称 | 人教版八年级数学上册 12.3角的平分线的性质 教学课件(共20张PPT)) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 16:55:53 | ||
图片预览



文档简介
(共20张PPT)
角的平分线的性质
学习目标
有理数的加法
1.学会尺规作图—画角平分线,并运用三角形全等的判定方法证明;
2.学会用角平分线的性质定理进行推理证明,培养学生的推理能力;
3.学会用角平分线的判定定理进行推理证明,拓宽学生几何证明的思路;
4.通过对角平分线相关知识的探究,培养学生逻辑推理能力,增强学生的严谨性.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
情景导入
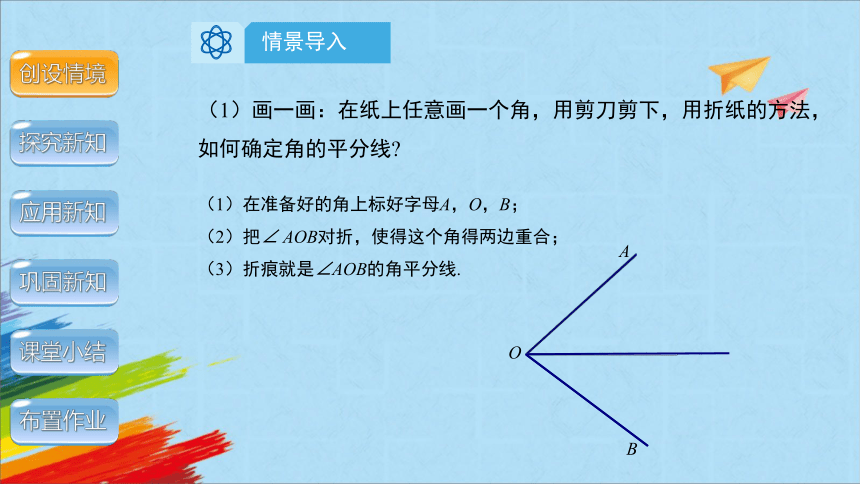
(1)画一画:在纸上任意画一个角,用剪刀剪下,用折纸的方法,如何确定角的平分线
(1)在准备好的角上标好字母A,O,B;
(2)把∠ AOB对折,使得这个角得两边重合;
(3)折痕就是∠AOB的角平分线.
A
O
B
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
情景导入
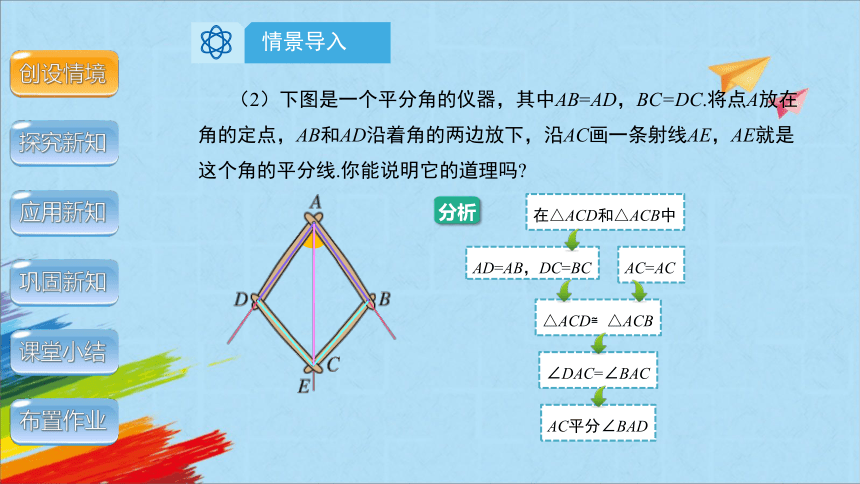
(2)下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的定点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线.你能说明它的道理吗
分析
在△ACD和△ACB中
AD=AB,DC=BC
△ACD≌△ACB
∠DAC=∠BAC
AC平分∠BAD
AC=AC
应用新知
巩固新知
课堂小结
布置作业
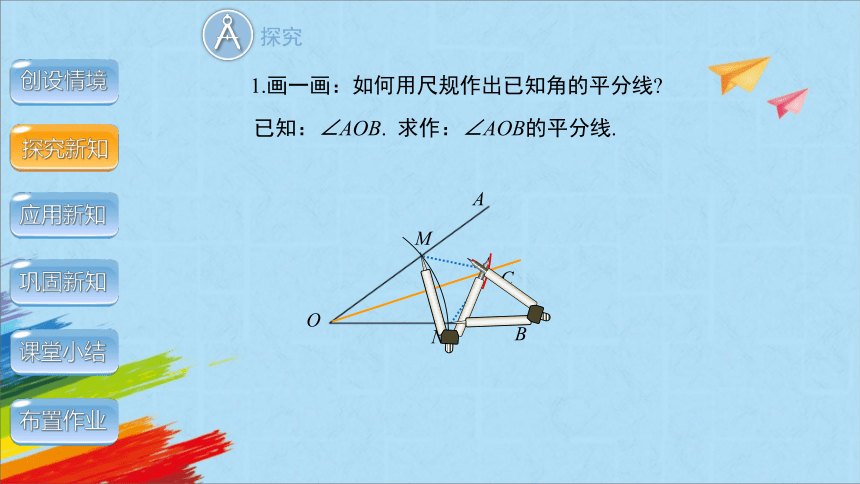
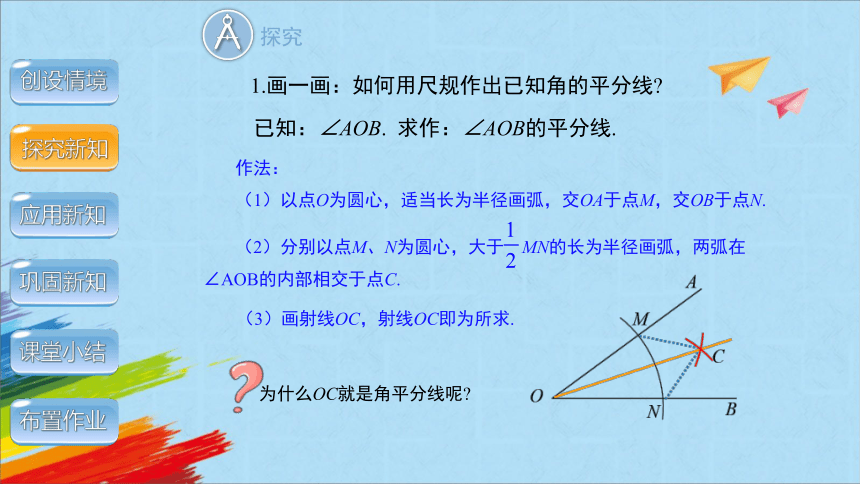
1.画一画:如何用尺规作出已知角的平分线
已知:∠AOB. 求作:∠AOB的平分线.
探究新知
创设情境
A
B
O
M
N
C
探究
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
为什么OC就是角平分线呢
探究
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
1.画一画:如何用尺规作出已知角的平分线
已知:∠AOB. 求作:∠AOB的平分线.
(2)分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC,射线OC即为所求.
应用新知
巩固新知
课堂小结
布置作业
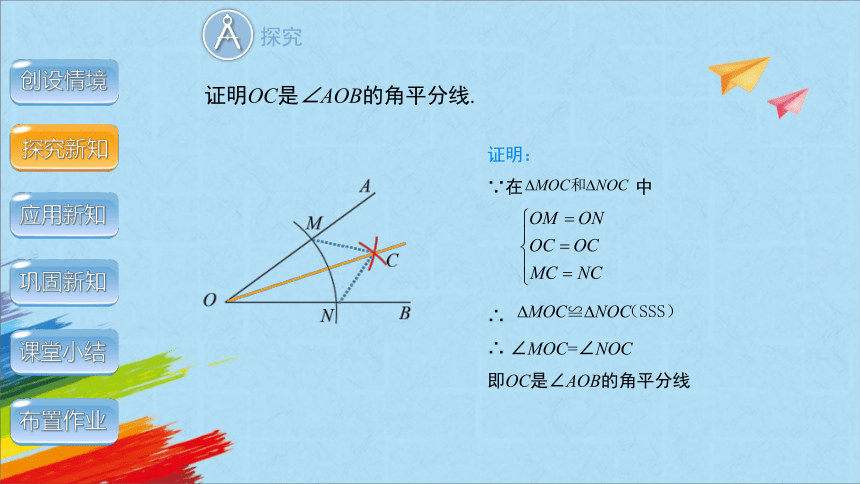
证明OC是∠AOB的角平分线.
探究新知
创设情境
证明:
∵在 中
∴
∴ ∠MOC=∠NOC
即OC是∠AOB的角平分线
探究
应用新知
巩固新知
课堂小结
布置作业
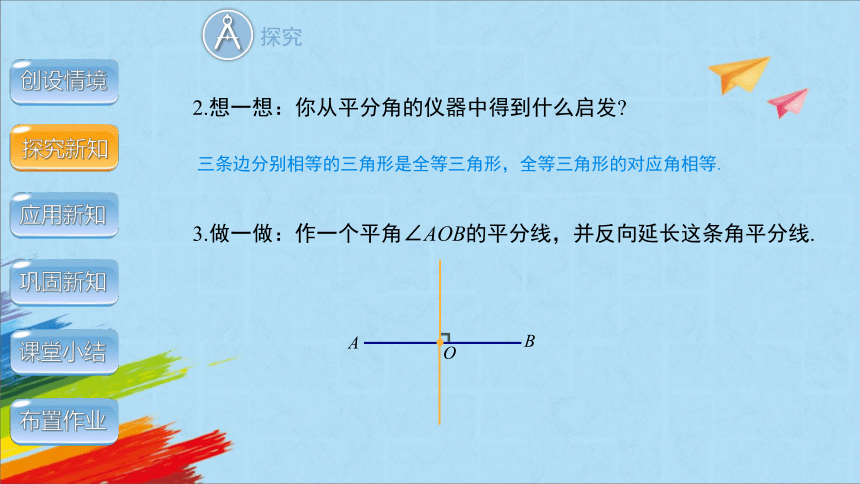
2.想一想:你从平分角的仪器中得到什么启发
3.做一做:作一个平角∠AOB的平分线,并反向延长这条角平分线.
三条边分别相等的三角形是全等三角形,全等三角形的对应角相等.
探究新知
创设情境
探究
A
O
B
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
例1:如图,任意作一个角∠AOB,作出∠AOB 的平分线OC.在OC上任意取一点P,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.
同学甲
同学乙
同学甲、乙谁的画法是正确的
PD=PE
探究
规律
角的平分线上的点到角的两边的距离相等.
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
做一做:你能用三角形全等证明这个结论吗
已知:如图,OC是∠AOB的平分线,P是OC上任意一点,做PD⊥OA,PE⊥OB,垂足分别是D,E.求证:PD=PE.
要证明PD=PE,只要证明它们所在的△OPD≌△OPE,而△OPD≌△OPE的条件由已知容易得到它满足公理(AAS).故结论可证.
分析:
思考
创设情境
巩固新知
课堂小结
布置作业
探究新知
如图,△ABC的角平分线BM,CN相交于点P.求证:点P到三边AB,BC,CA的距离相等.
应用新知
证明:
过点P作PD,PE,PF分别垂直于AB,BC,CA垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理 PE=PF
∴PD=PE=PF
即点P到三边AB,BC,CA的距离相等.
D
E
F
典型例题
创设情境
巩固新知
课堂小结
布置作业
探究新知
想一想:点P在∠A的平分线上吗 这说明三角形的三条角平分线有什么关系
应用新知
在
由上面可知:PD=PE=PF
在Rt△PDA和Rt△PFA中,
PD=PF,PA=PA
∴ Rt△PDA≌Rt△PFA(HL)
∴∠PAD=∠PAF
∴PA平分∠BAC
三角形的三条角平分线交于一点.
典型例题
创设情境
巩固新知
课堂小结
布置作业
探究新知
例2:如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)
应用新知
B
A
S
C
D
M
N
AB:500=1: 20 000
AB=2.5cm
典型例题
规律
创设情境
巩固新知
课堂小结
布置作业
探究新知
应用新知
角的内部到角的两边的距离相等的点在角的平分线上.
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1∶20 000)
B
A
S
C
D
在Rt△ABC与Rt△ABD中:
∴ Rt△ABC ≌ Rt△ABD(HL).
AB=AB
BC=BD
∠CAB=∠DAB
点B在∠CAD的角平分线上
AB:500=1: 20 000
AB=2.5cm
M
N
典型例题
创设情境
巩固新知
课堂小结
布置作业
探究新知
归纳
角的平分线的性质
角的平分线上的点到角的两边的距离相等.
应用新知
角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等.
如上右图,作∠AOB的角平分线,与MN交于点,点P即为所求.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P.
求证:点P到三边AB,BC,CA所在直线的距离相等.
证明:
∵ △ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P,作PF⊥AC, PG⊥BC,PH⊥AB,
H
F
G
∴PF=PG,PG=PH
∴PF=PG=PH,
∴点P到三边AB,BC,CA所在直线的距离相等.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
三角形的角平分线
尺规作图
性质定理
判定定理
角的平分线上的点到角的两边的距离相等.
角的内部到角的两边的距离相等的点在角的平分线上.
布置作业
习题12.3第1~5题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
角的平分线的性质
学习目标
有理数的加法
1.学会尺规作图—画角平分线,并运用三角形全等的判定方法证明;
2.学会用角平分线的性质定理进行推理证明,培养学生的推理能力;
3.学会用角平分线的判定定理进行推理证明,拓宽学生几何证明的思路;
4.通过对角平分线相关知识的探究,培养学生逻辑推理能力,增强学生的严谨性.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
情景导入
(1)画一画:在纸上任意画一个角,用剪刀剪下,用折纸的方法,如何确定角的平分线
(1)在准备好的角上标好字母A,O,B;
(2)把∠ AOB对折,使得这个角得两边重合;
(3)折痕就是∠AOB的角平分线.
A
O
B
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
情景导入
(2)下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的定点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线.你能说明它的道理吗
分析
在△ACD和△ACB中
AD=AB,DC=BC
△ACD≌△ACB
∠DAC=∠BAC
AC平分∠BAD
AC=AC
应用新知
巩固新知
课堂小结
布置作业
1.画一画:如何用尺规作出已知角的平分线
已知:∠AOB. 求作:∠AOB的平分线.
探究新知
创设情境
A
B
O
M
N
C
探究
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
为什么OC就是角平分线呢
探究
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
1.画一画:如何用尺规作出已知角的平分线
已知:∠AOB. 求作:∠AOB的平分线.
(2)分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC,射线OC即为所求.
应用新知
巩固新知
课堂小结
布置作业
证明OC是∠AOB的角平分线.
探究新知
创设情境
证明:
∵在 中
∴
∴ ∠MOC=∠NOC
即OC是∠AOB的角平分线
探究
应用新知
巩固新知
课堂小结
布置作业
2.想一想:你从平分角的仪器中得到什么启发
3.做一做:作一个平角∠AOB的平分线,并反向延长这条角平分线.
三条边分别相等的三角形是全等三角形,全等三角形的对应角相等.
探究新知
创设情境
探究
A
O
B
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
例1:如图,任意作一个角∠AOB,作出∠AOB 的平分线OC.在OC上任意取一点P,过点P画出OA,OB的垂线,分别记垂足为D,E,测量PD,PE并作比较,你得到什么结论?在OC上再取几个点试一试.
同学甲
同学乙
同学甲、乙谁的画法是正确的
PD=PE
探究
规律
角的平分线上的点到角的两边的距离相等.
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
做一做:你能用三角形全等证明这个结论吗
已知:如图,OC是∠AOB的平分线,P是OC上任意一点,做PD⊥OA,PE⊥OB,垂足分别是D,E.求证:PD=PE.
要证明PD=PE,只要证明它们所在的△OPD≌△OPE,而△OPD≌△OPE的条件由已知容易得到它满足公理(AAS).故结论可证.
分析:
思考
创设情境
巩固新知
课堂小结
布置作业
探究新知
如图,△ABC的角平分线BM,CN相交于点P.求证:点P到三边AB,BC,CA的距离相等.
应用新知
证明:
过点P作PD,PE,PF分别垂直于AB,BC,CA垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理 PE=PF
∴PD=PE=PF
即点P到三边AB,BC,CA的距离相等.
D
E
F
典型例题
创设情境
巩固新知
课堂小结
布置作业
探究新知
想一想:点P在∠A的平分线上吗 这说明三角形的三条角平分线有什么关系
应用新知
在
由上面可知:PD=PE=PF
在Rt△PDA和Rt△PFA中,
PD=PF,PA=PA
∴ Rt△PDA≌Rt△PFA(HL)
∴∠PAD=∠PAF
∴PA平分∠BAC
三角形的三条角平分线交于一点.
典型例题
创设情境
巩固新知
课堂小结
布置作业
探究新知
例2:如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)
应用新知
B
A
S
C
D
M
N
AB:500=1: 20 000
AB=2.5cm
典型例题
规律
创设情境
巩固新知
课堂小结
布置作业
探究新知
应用新知
角的内部到角的两边的距离相等的点在角的平分线上.
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1∶20 000)
B
A
S
C
D
在Rt△ABC与Rt△ABD中:
∴ Rt△ABC ≌ Rt△ABD(HL).
AB=AB
BC=BD
∠CAB=∠DAB
点B在∠CAD的角平分线上
AB:500=1: 20 000
AB=2.5cm
M
N
典型例题
创设情境
巩固新知
课堂小结
布置作业
探究新知
归纳
角的平分线的性质
角的平分线上的点到角的两边的距离相等.
应用新知
角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等.
如上右图,作∠AOB的角平分线,与MN交于点,点P即为所求.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P.
求证:点P到三边AB,BC,CA所在直线的距离相等.
证明:
∵ △ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P,作PF⊥AC, PG⊥BC,PH⊥AB,
H
F
G
∴PF=PG,PG=PH
∴PF=PG=PH,
∴点P到三边AB,BC,CA所在直线的距离相等.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
三角形的角平分线
尺规作图
性质定理
判定定理
角的平分线上的点到角的两边的距离相等.
角的内部到角的两边的距离相等的点在角的平分线上.
布置作业
习题12.3第1~5题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
