人教版八年级数学上册12.2三角形全等的判定 第2课时 教学课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.2三角形全等的判定 第2课时 教学课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
三角形全等的判定
第二课时
学习目标
三角形全等的判定
掌握全等三角形的判定方法(SAS);
了解利用SSA不一定能证明三角形全等;
经历动手操作(已知两边及夹角能确定唯一三角形)这一过程,培养学生直观想象的思维能力;
通过探究对给定的两边及一角来确定三角形的形状和大小是否唯一这一过程,培养学生分析问题、解决问题的能力。
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
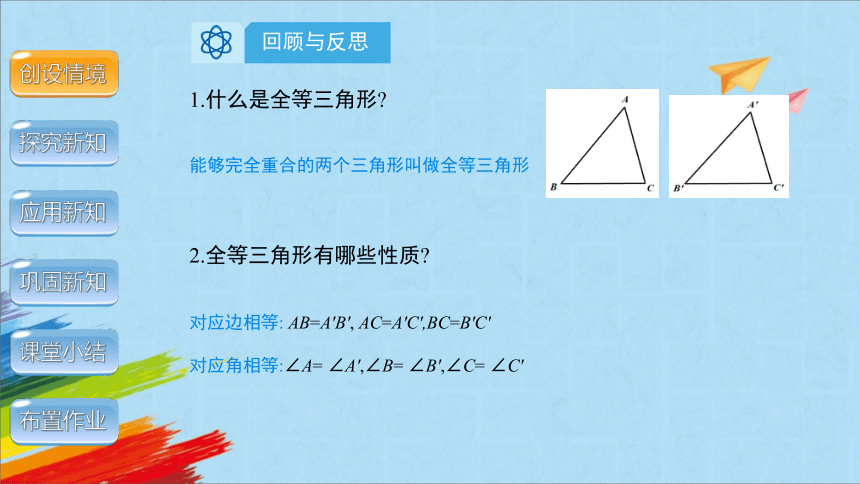
1.什么是全等三角形
2.全等三角形有哪些性质
回顾与反思
对应边相等: AB=A'B', AC=A'C',BC=B'C'
对应角相等:∠A= ∠A',∠B= ∠B',∠C= ∠C'
能够完全重合的两个三角形叫做全等三角形
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
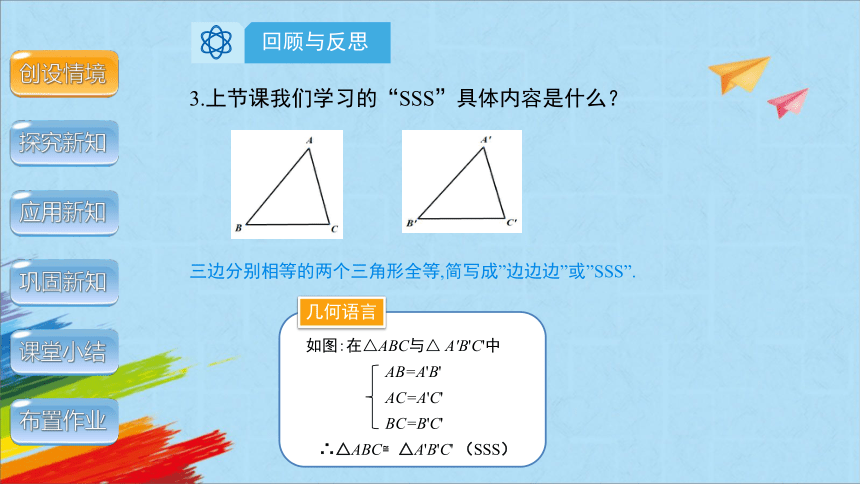
3.上节课我们学习的“SSS”具体内容是什么?
回顾与反思
三边分别相等的两个三角形全等,简写成”边边边”或”SSS”.
几何语言
如图:在△ABC与△ A'B'C'中
AB=A'B'
AC=A'C'
BC=B'C'
∴△ABC≌△A'B'C' (SSS)
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
已知△ABC,你能再画一个△A'B'C',使AB=A'B',∠B=∠B',BC=B'C'吗
(2)在射线A′D上截取A′B′=AB,
在射线A′E上截取A′C′=AC;
A′
C′
B′
画法:
(3)连接B′C′.
(1)画∠DA′E=∠A;
E
D
A
B
C
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
操作
(1)把画好的三角形剪下和原三角形重叠,观察能重合在一起吗
A′
C′
B′
E
D
A
B
C
完全重合
结论
两边和它们的夹角分别相等的两个三角形全等.
边角边
SAS
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC .固定住长木棍,转动短木棍,得到△ABD ,这个实验说明了什么?
结论
A
B
C
D
A
B
C
D
两边和其中一边的对角分别相等的两个三角形
不一定全等.
SSA
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
结论:
两边和它们的夹角分别相等的两个三角形全等,简写成”边角边”或”SAS”.
几何语言:
如图,在△ABC与△ A'B'C'中:
∴△ABC≌△A'B'C'(SAS)
AB=A'B'
∠A=∠A'
AC=A'C'
两边和其中一边的对角分别相等的两个三角形不一定全等.
探究新知
新课导入
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2 如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离,为什么
分析:如果能够证明△ABC≌△DEC,就可以得出AB=DE
探究新知
新课导入
巩固新知
课堂小结
布置作业
应用新知
典型例题
分析实际问题,按要求画出图形,根据图形及已知条件选择对应的方法.
对顶角相等
证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS)
∴AB=DE
∠1=∠2
解决实际问题的一般方法是:
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,AD=AE,若利用“SAS”证明△ABE和△ACD全等,则需要添加的条件是( )
A.AD=AE
B.∠B=∠C
C.∠AEB=∠ADC
D.∠A=∠B
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,BC⊥AC, BD⊥AD,且AB平分∠CAD,则利用( )可证明△ABC和△ABD全等.
A.AAS
B.ASA
C.SAS
D.SSA
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,已知AB=AC,点D,E分别是AB和AC上的点,且DB=EC.求证:∠B=∠C.
证明:
∵AB=AC,DB=EC
∴AD=AE
在△ABE和△ACD中,
∴ △ABE≌△ACD (SAS)
∴∠B=∠C
两边和其中一边的对角分别相等的两个三角形不一定全等.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
三角形全等的判定SAS
SAS
SSA
两边和它们的夹角分别相等的两个三角形全等
布置作业
教科书习题12.2
第3,4题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
三角形全等的判定
第二课时
学习目标
三角形全等的判定
掌握全等三角形的判定方法(SAS);
了解利用SSA不一定能证明三角形全等;
经历动手操作(已知两边及夹角能确定唯一三角形)这一过程,培养学生直观想象的思维能力;
通过探究对给定的两边及一角来确定三角形的形状和大小是否唯一这一过程,培养学生分析问题、解决问题的能力。
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
1.什么是全等三角形
2.全等三角形有哪些性质
回顾与反思
对应边相等: AB=A'B', AC=A'C',BC=B'C'
对应角相等:∠A= ∠A',∠B= ∠B',∠C= ∠C'
能够完全重合的两个三角形叫做全等三角形
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
3.上节课我们学习的“SSS”具体内容是什么?
回顾与反思
三边分别相等的两个三角形全等,简写成”边边边”或”SSS”.
几何语言
如图:在△ABC与△ A'B'C'中
AB=A'B'
AC=A'C'
BC=B'C'
∴△ABC≌△A'B'C' (SSS)
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
已知△ABC,你能再画一个△A'B'C',使AB=A'B',∠B=∠B',BC=B'C'吗
(2)在射线A′D上截取A′B′=AB,
在射线A′E上截取A′C′=AC;
A′
C′
B′
画法:
(3)连接B′C′.
(1)画∠DA′E=∠A;
E
D
A
B
C
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
操作
(1)把画好的三角形剪下和原三角形重叠,观察能重合在一起吗
A′
C′
B′
E
D
A
B
C
完全重合
结论
两边和它们的夹角分别相等的两个三角形全等.
边角边
SAS
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC .固定住长木棍,转动短木棍,得到△ABD ,这个实验说明了什么?
结论
A
B
C
D
A
B
C
D
两边和其中一边的对角分别相等的两个三角形
不一定全等.
SSA
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
结论:
两边和它们的夹角分别相等的两个三角形全等,简写成”边角边”或”SAS”.
几何语言:
如图,在△ABC与△ A'B'C'中:
∴△ABC≌△A'B'C'(SAS)
AB=A'B'
∠A=∠A'
AC=A'C'
两边和其中一边的对角分别相等的两个三角形不一定全等.
探究新知
新课导入
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2 如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离,为什么
分析:如果能够证明△ABC≌△DEC,就可以得出AB=DE
探究新知
新课导入
巩固新知
课堂小结
布置作业
应用新知
典型例题
分析实际问题,按要求画出图形,根据图形及已知条件选择对应的方法.
对顶角相等
证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS)
∴AB=DE
∠1=∠2
解决实际问题的一般方法是:
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,AD=AE,若利用“SAS”证明△ABE和△ACD全等,则需要添加的条件是( )
A.AD=AE
B.∠B=∠C
C.∠AEB=∠ADC
D.∠A=∠B
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,BC⊥AC, BD⊥AD,且AB平分∠CAD,则利用( )可证明△ABC和△ABD全等.
A.AAS
B.ASA
C.SAS
D.SSA
A
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,已知AB=AC,点D,E分别是AB和AC上的点,且DB=EC.求证:∠B=∠C.
证明:
∵AB=AC,DB=EC
∴AD=AE
在△ABE和△ACD中,
∴ △ABE≌△ACD (SAS)
∴∠B=∠C
两边和其中一边的对角分别相等的两个三角形不一定全等.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
三角形全等的判定SAS
SAS
SSA
两边和它们的夹角分别相等的两个三角形全等
布置作业
教科书习题12.2
第3,4题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
