人教版八年级数学上册12.2《三角形全等的判定》第3课时 教学课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.2《三角形全等的判定》第3课时 教学课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
三角形全等的判定
第三课时
学习目标
三角形全等的判定
掌握全等三角形的判定方法(ASA)及(AAS);
通过类比的方法继续探究对于给定的两角及一边的三角形是否唯一确定;
经历动手操作(已知两角及一边能确定唯一三角形)这一过程,培养学生直观想象的思维能力;
通过探究对给定的两角及一边来确定三角形的形状和大小是否唯一这一过程,培养学生分析问题、解决问题的能力。
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
(1)三角形中已知三个元素,包括哪几种情况
(2)到目前为止,可以作为判定两个三角形全等的方法有几种
各是什么
回顾与反思
①三个角分别对应相等
2种
②三条边分别对应相等
③两边一角:
两条边及其夹角对应相等;
两条边及一边的对角分别相等
④两角一边
两个角及其夹边分别相等
两个角及一角的对边分别相等
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
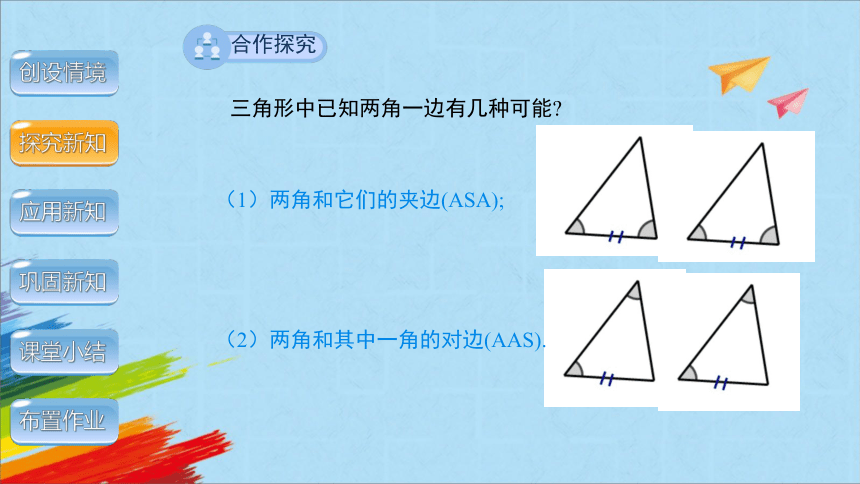
三角形中已知两角一边有几种可能
(1)两角和它们的夹边(ASA);
(2)两角和其中一角的对边(AAS).
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
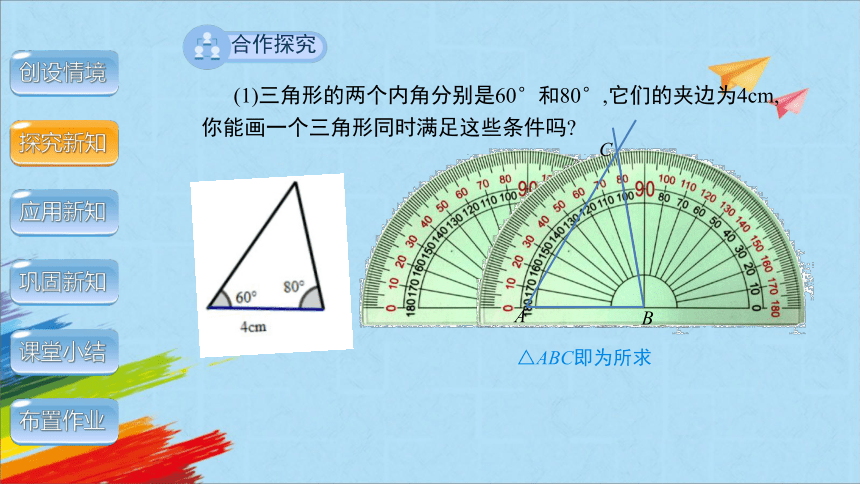
(1)三角形的两个内角分别是60°和80°,它们的夹边为4cm,你能画一个三角形同时满足这些条件吗
A
B
C
△ABC即为所求
结论
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
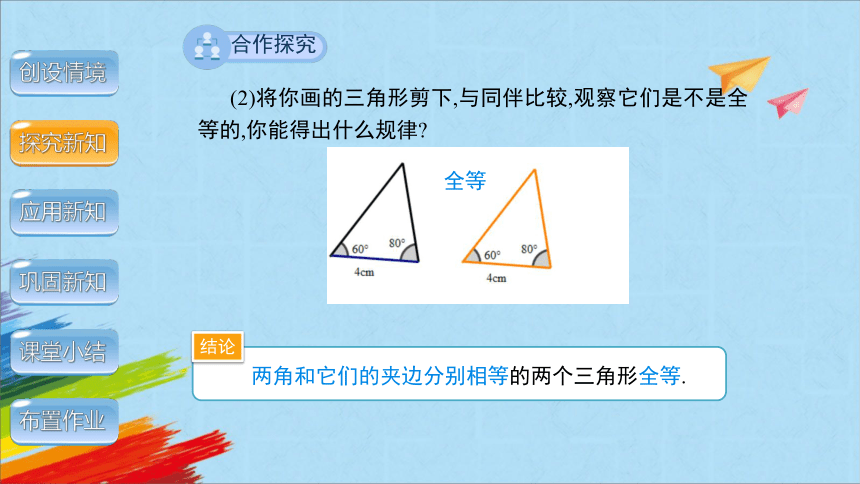
两角和它们的夹边分别相等的两个三角形全等.
全等
(2)将你画的三角形剪下,与同伴比较,观察它们是不是全等的,你能得出什么规律
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
A′
B′
C′
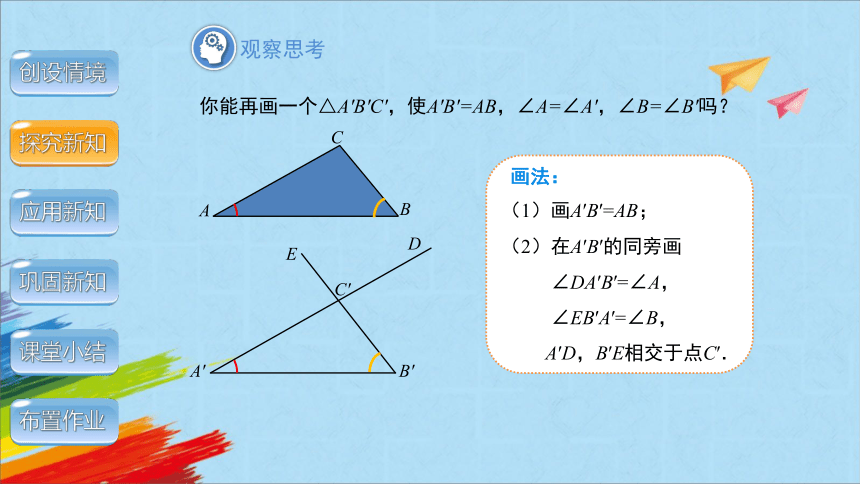
画法:
E
(1)画A′B′=AB;
(2)在A′B′的同旁画
∠DA′B′=∠A,
∠EB′A′=∠B,
A′D,B′E相交于点C′.
D
C
A
B
你能再画一个△A'B'C',使A'B'=AB,∠A=∠A',∠B=∠B'吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
A′
B′
C′
E
D
C
A
B
完全重合
两角和它们的夹边分别相等的两个三角形全等.
几何语言
如图,在△ABC与△ A′B′C′中:
∴△ABC≌△A′B′C′(ASA).
∠A=∠A'
AB=A′B′
∠B=∠B'
角边角
ASA
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗 能利用角边角条件证明你的结论吗
证明:
∵∠A+∠B+∠C=∠D+∠E+∠F=180°,∠A=∠D,∠B=∠E,
∴∠A+∠B=∠D+∠E.
∴∠C=∠F.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
两角分别相等且其中一组等角的对边相等的两个三角形全等
归纳
角角边
AAS
几何语言:
如图,在△ABC与△ DEF中:
∴△ABC △DEF(AAS).
∠A=∠D
AC=DF
∠B=∠E
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
三角形全等的判定方法
1.两角和它们的夹边分别相等的两个三角形全等(可以简写成”角边角”或”ASA”).
2.两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成”角角边”或”AAS”).
探究新知
新课导入
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1 如下图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE
分析:AD和AE分别在△ADC和△AEB中,所以要证AD=AE,只需证明△ADC≌△AEB即可.
证明:在△ADC和△AEB中,
∴△ADC≌△AEB(ASA)
∴AD=AE
探究新知
新课导入
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2.如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.求证AB=CD.
证明:
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
在△ ABC和△ ADC中,
∴ △ABC≌ △ADC(AAS),
∴AB=CD.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是( )
A.AAS
B.ASA
C.SAS
D.SSS
B
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,∠ABC=∠DCB,只需补充条件__________;就可以根据“AAS”得到△ABC≌△DCB.
∠A=∠D
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长.为什么
解析:
∵AB⊥BF,DE⊥BF,
∴∠B=∠EDC=90°.
在△ ABC和△ EDC中,
∴ △ ABC≌ △ EDC(ASA)
∴AB=ED.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
两角分别相等且其中一组等角的对边相等的两个三角形全等.
三角形全等的判ASA/AAS
ASA
AAS
两角和它们的夹边分别相等的两个三角形全等.
C
A
B
A′
B′
C′
布置作业
习题12.2第5题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
三角形全等的判定
第三课时
学习目标
三角形全等的判定
掌握全等三角形的判定方法(ASA)及(AAS);
通过类比的方法继续探究对于给定的两角及一边的三角形是否唯一确定;
经历动手操作(已知两角及一边能确定唯一三角形)这一过程,培养学生直观想象的思维能力;
通过探究对给定的两角及一边来确定三角形的形状和大小是否唯一这一过程,培养学生分析问题、解决问题的能力。
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
(1)三角形中已知三个元素,包括哪几种情况
(2)到目前为止,可以作为判定两个三角形全等的方法有几种
各是什么
回顾与反思
①三个角分别对应相等
2种
②三条边分别对应相等
③两边一角:
两条边及其夹角对应相等;
两条边及一边的对角分别相等
④两角一边
两个角及其夹边分别相等
两个角及一角的对边分别相等
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
三角形中已知两角一边有几种可能
(1)两角和它们的夹边(ASA);
(2)两角和其中一角的对边(AAS).
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
(1)三角形的两个内角分别是60°和80°,它们的夹边为4cm,你能画一个三角形同时满足这些条件吗
A
B
C
△ABC即为所求
结论
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
合作探究
两角和它们的夹边分别相等的两个三角形全等.
全等
(2)将你画的三角形剪下,与同伴比较,观察它们是不是全等的,你能得出什么规律
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
A′
B′
C′
画法:
E
(1)画A′B′=AB;
(2)在A′B′的同旁画
∠DA′B′=∠A,
∠EB′A′=∠B,
A′D,B′E相交于点C′.
D
C
A
B
你能再画一个△A'B'C',使A'B'=AB,∠A=∠A',∠B=∠B'吗?
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
A′
B′
C′
E
D
C
A
B
完全重合
两角和它们的夹边分别相等的两个三角形全等.
几何语言
如图,在△ABC与△ A′B′C′中:
∴△ABC≌△A′B′C′(ASA).
∠A=∠A'
AB=A′B′
∠B=∠B'
角边角
ASA
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗 能利用角边角条件证明你的结论吗
证明:
∵∠A+∠B+∠C=∠D+∠E+∠F=180°,∠A=∠D,∠B=∠E,
∴∠A+∠B=∠D+∠E.
∴∠C=∠F.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
两角分别相等且其中一组等角的对边相等的两个三角形全等
归纳
角角边
AAS
几何语言:
如图,在△ABC与△ DEF中:
∴△ABC △DEF(AAS).
∠A=∠D
AC=DF
∠B=∠E
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
归纳
三角形全等的判定方法
1.两角和它们的夹边分别相等的两个三角形全等(可以简写成”角边角”或”ASA”).
2.两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成”角角边”或”AAS”).
探究新知
新课导入
巩固新知
课堂小结
布置作业
应用新知
典型例题
例1 如下图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE
分析:AD和AE分别在△ADC和△AEB中,所以要证AD=AE,只需证明△ADC≌△AEB即可.
证明:在△ADC和△AEB中,
∴△ADC≌△AEB(ASA)
∴AD=AE
探究新知
新课导入
巩固新知
课堂小结
布置作业
应用新知
典型例题
例2.如图,AB⊥BC,AD⊥DC,垂足分别为B,D,∠1=∠2.求证AB=CD.
证明:
∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
在△ ABC和△ ADC中,
∴ △ABC≌ △ADC(AAS),
∴AB=CD.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
1.如图,用纸板挡住了三角形的一部分,小明根据所学知识很快就画出了一个与原来完全一样的三角形,他的依据是( )
A.AAS
B.ASA
C.SAS
D.SSS
B
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
2.如图,∠ABC=∠DCB,只需补充条件__________;就可以根据“AAS”得到△ABC≌△DCB.
∠A=∠D
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
3.如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长.为什么
解析:
∵AB⊥BF,DE⊥BF,
∴∠B=∠EDC=90°.
在△ ABC和△ EDC中,
∴ △ ABC≌ △ EDC(ASA)
∴AB=ED.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
两角分别相等且其中一组等角的对边相等的两个三角形全等.
三角形全等的判ASA/AAS
ASA
AAS
两角和它们的夹边分别相等的两个三角形全等.
C
A
B
A′
B′
C′
布置作业
习题12.2第5题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
