人教版八年级数学上册14.2.2完全平方公式 第2课时 教学课件(共22张PPT)
文档属性
| 名称 | 人教版八年级数学上册14.2.2完全平方公式 第2课时 教学课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 16:45:34 | ||
图片预览






文档简介
(共22张PPT)
14.2.2 完全平方公式
第2课时
学习目标
1.类比去括号法则,理解并掌握添括号法则;
2.能灵活运用添括号法则对式子进行变形,并能灵活运用乘法公式进行计算;
3.通过添括号法则的探究,培养学生类比归纳的数学思想;
4.经历添括号法则的推导过程,体会数学逻辑思维的缜密性,锻炼学生的表达能力.
添
括
号
法
则
复习回顾
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
平方差公式
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
符号语言
文字语言
(a+b)(a b)=a2 b2
复习回顾
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
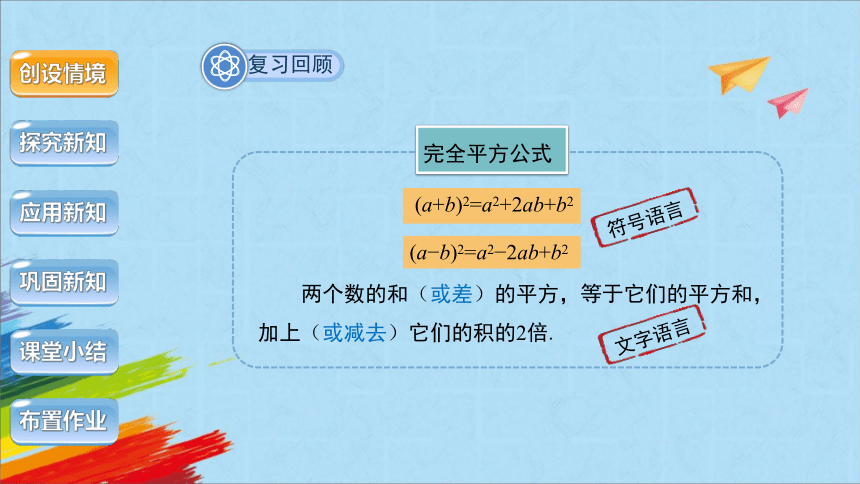
完全平方公式
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
符号语言
文字语言
复习回顾
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
去括号法则
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
你还记得去括号法则吗?试着去掉下面式子中的括号.
a+(b+c)=
a–(b+c)=
a+b+c
a–b–c
有时要在式子中添括号,如何添括号呢?
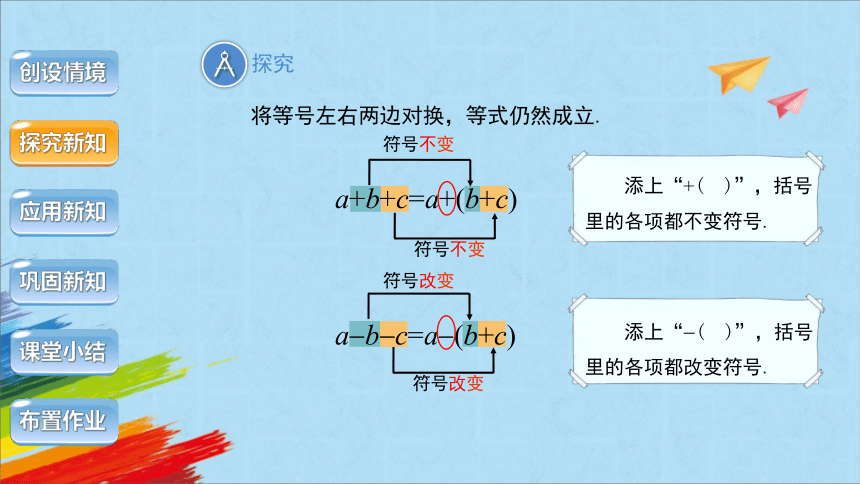
将等号左右两边对换,等式仍然成立.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
a+b+c
=
a+(b+c)
a b c
=
a (b+c)
你能类比去括号法则
总结出添括号法则吗?
小组合作
1.独立思考,完成验证;
2.两人一组,交流思路,完善过程.
将等号左右两边对换,等式仍然成立.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
a+b+c=a+(b+c)
a b c=a (b+c)
符号不变
符号不变
添上“+( )”,括号里的各项都不变符号.
符号改变
符号改变
添上“ ( )”,括号里的各项都改变符号.
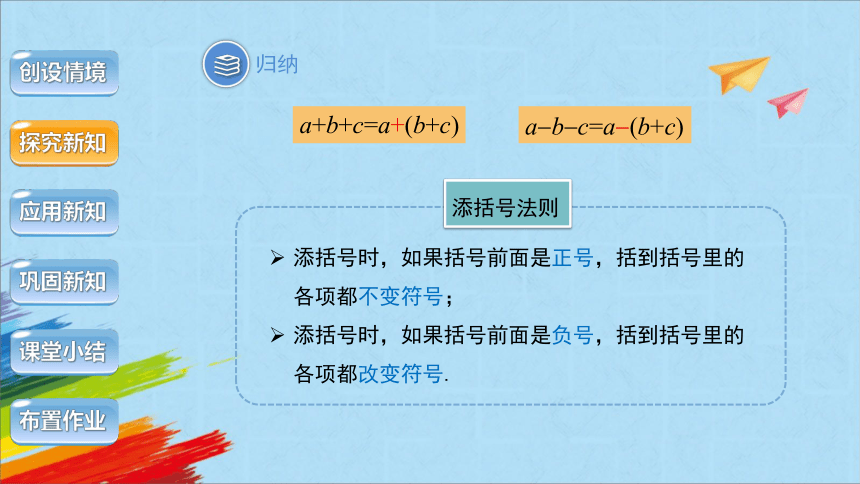
归纳
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
添括号法则
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;
添括号时,如果括号前面是负号,括到括号里的各项都改变符号.
a+b+c=a+(b+c)
a b c=a (b+c)
做一做
在等号右边的括号内填上合适的项.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
(1) a+b c=a+( );
(2) a b+c=a ( );
(3) 2a 2b c=2a ( );
(4) 2x+3y 2=2x+( ).
b c
b c
2b+c
3y 2
括号前面是正号,括到括号里的各项都不变符号.
括号前面是负号,括到括号里的各项都改变符号.
延伸
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
无论是添括号还是去括号,只改变式子的形式,不改变式子的值,是恒等变形.
添括号是否正确,可利用去括号法则检验.
添括号时,如果括号前面是负号,括到括号里的各项都改变符号,而不是只改变括号里的第一项的符号.
1
2
3
添括号是添上括号和括号前面的符号. 括号前面的“+”或
“ ”不是原来多项式的某一项的符号“移”出来的.
4
运用添括号法则的注意事项
想一想
下列式子是否能用乘法公式计算?
(1) (m+n+1)(m+n 1)
(2) ( m+n 1)(m+n 1)
能
[(m+n)+1][ (m+n) 1]
能
[(n 1) m][(n 1)+m]
=(m+n)2 12
=(n 1)2 m2
可通过添括号变形成乘法公式的形式,将其中某一部分看作一项.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
【例】运用乘法公式计算:
(1) (x+2y 3)(x 2y+3); (2) (a+b+c)2 .
创设情境
解:(1) (x+2y 3)(x 2y+3)
=[x+(2y 3)][x (2y 3)]
=x2 (2y 3)2
=x2 (4y2 12y+9)
=x2 4y2+12y 9;
有些整式相乘需要先作适当变形,然后再用公式.
将2y 3看作整体
运用添括号法则变形成乘法公式的形式
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
【例】运用乘法公式计算:
(1) (x+2y 3)(x 2y+3); (2) (a+b+c)2 .
创设情境
解:(2) (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc .
将a+b看作整体
括号前面是正号,括到括号里的各项都不变符号.
还有其它的添括号的方法吗?
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
(a+b+c)2
=[a+(b+c)]2
=a2+2a(b+c)+(b+c)2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c)2
=[b+(a+c)]2
=b2+2b(a+c)+(a+c)2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c)2 =a2+b2+c2+2ab+2ac+2bc
完全平方公式的推广
拓展
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
1.在等号右边的括号内填上合适的项,并用去括号法则检验.
(1) x2 x+1 = x2 ( );
(2) 2x2 3x 1= 2x2+( );
(3) a 2b 4c+5=(a 2b) ( ) ;
(4) (a b) (c d)=a ( ) .
4c 5
x 1
3x 1
b+c d
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
2.运用乘法公式计算:
(1) ( m+n+1)(m+n 1) (2) (a 2b 1)2
解: (1) ( m+n+1)(m+n 1)
=[n (m 1)][n+ (m 1)]
=n2 (m 1)2
=n2 (m2 2m+1)
=n2 m2+2m 1
(3) (x y m+n)(x y+m n)
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
2.运用乘法公式计算:
(1) ( m+n+1)(m+n 1) (2) (a 2b 1)2
解: (2) (a 2b 1)2
=[(a 2b) 1]2
=(a 2b)2 2(a 2b)+12
=a2 4ab+4b2 2a+4b+1
也可变形为[a (2b+1)]2
(3) (x y m+n)(x y+m n)
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
解:(3) (x y m+n)(x y+m n)
=[(x y) (m n)][(x y)+(m n)]
=(x y)2 (m n)2
=x2 2xy+y2 m2+2mn n2
2.运用乘法公式计算:
(1) ( m+n+1)(m+n 1) (2) (a 2b 1)2
(3) (x y m+n)(x y+m n)
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
3.灵活运用乘法公式计算:
已知(m+n+1)(m+n 1)=63,则m+n= .
解:∵ (m+n+1)(m+n 1)
=(m+n)2 12=63
∴(m+n)2=64
∴m+n= 8
8
注意:
添括号法则:
添
括
号
法
则
巩固新知
课堂小结
应用新知
探究新知
布置作业
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
创设情境
有些整式相乘需要先通过添括号作适当变形,然后再灵活运用乘法公式计算.
布置作业
教科书第111页
练习第2题
第112页
习题14.2第3题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
14.2.2 完全平方公式
第2课时
学习目标
1.类比去括号法则,理解并掌握添括号法则;
2.能灵活运用添括号法则对式子进行变形,并能灵活运用乘法公式进行计算;
3.通过添括号法则的探究,培养学生类比归纳的数学思想;
4.经历添括号法则的推导过程,体会数学逻辑思维的缜密性,锻炼学生的表达能力.
添
括
号
法
则
复习回顾
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
平方差公式
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
符号语言
文字语言
(a+b)(a b)=a2 b2
复习回顾
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
完全平方公式
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
符号语言
文字语言
复习回顾
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
去括号法则
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
你还记得去括号法则吗?试着去掉下面式子中的括号.
a+(b+c)=
a–(b+c)=
a+b+c
a–b–c
有时要在式子中添括号,如何添括号呢?
将等号左右两边对换,等式仍然成立.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
a+b+c
=
a+(b+c)
a b c
=
a (b+c)
你能类比去括号法则
总结出添括号法则吗?
小组合作
1.独立思考,完成验证;
2.两人一组,交流思路,完善过程.
将等号左右两边对换,等式仍然成立.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究
a+b+c=a+(b+c)
a b c=a (b+c)
符号不变
符号不变
添上“+( )”,括号里的各项都不变符号.
符号改变
符号改变
添上“ ( )”,括号里的各项都改变符号.
归纳
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
添括号法则
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;
添括号时,如果括号前面是负号,括到括号里的各项都改变符号.
a+b+c=a+(b+c)
a b c=a (b+c)
做一做
在等号右边的括号内填上合适的项.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
(1) a+b c=a+( );
(2) a b+c=a ( );
(3) 2a 2b c=2a ( );
(4) 2x+3y 2=2x+( ).
b c
b c
2b+c
3y 2
括号前面是正号,括到括号里的各项都不变符号.
括号前面是负号,括到括号里的各项都改变符号.
延伸
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
无论是添括号还是去括号,只改变式子的形式,不改变式子的值,是恒等变形.
添括号是否正确,可利用去括号法则检验.
添括号时,如果括号前面是负号,括到括号里的各项都改变符号,而不是只改变括号里的第一项的符号.
1
2
3
添括号是添上括号和括号前面的符号. 括号前面的“+”或
“ ”不是原来多项式的某一项的符号“移”出来的.
4
运用添括号法则的注意事项
想一想
下列式子是否能用乘法公式计算?
(1) (m+n+1)(m+n 1)
(2) ( m+n 1)(m+n 1)
能
[(m+n)+1][ (m+n) 1]
能
[(n 1) m][(n 1)+m]
=(m+n)2 12
=(n 1)2 m2
可通过添括号变形成乘法公式的形式,将其中某一部分看作一项.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
【例】运用乘法公式计算:
(1) (x+2y 3)(x 2y+3); (2) (a+b+c)2 .
创设情境
解:(1) (x+2y 3)(x 2y+3)
=[x+(2y 3)][x (2y 3)]
=x2 (2y 3)2
=x2 (4y2 12y+9)
=x2 4y2+12y 9;
有些整式相乘需要先作适当变形,然后再用公式.
将2y 3看作整体
运用添括号法则变形成乘法公式的形式
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
【例】运用乘法公式计算:
(1) (x+2y 3)(x 2y+3); (2) (a+b+c)2 .
创设情境
解:(2) (a+b+c)2
=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc .
将a+b看作整体
括号前面是正号,括到括号里的各项都不变符号.
还有其它的添括号的方法吗?
探究新知
巩固新知
课堂小结
布置作业
应用新知
创设情境
(a+b+c)2
=[a+(b+c)]2
=a2+2a(b+c)+(b+c)2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c)2
=[b+(a+c)]2
=b2+2b(a+c)+(a+c)2
=a2+b2+c2+2ab+2ac+2bc
(a+b+c)2 =a2+b2+c2+2ab+2ac+2bc
完全平方公式的推广
拓展
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
1.在等号右边的括号内填上合适的项,并用去括号法则检验.
(1) x2 x+1 = x2 ( );
(2) 2x2 3x 1= 2x2+( );
(3) a 2b 4c+5=(a 2b) ( ) ;
(4) (a b) (c d)=a ( ) .
4c 5
x 1
3x 1
b+c d
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
2.运用乘法公式计算:
(1) ( m+n+1)(m+n 1) (2) (a 2b 1)2
解: (1) ( m+n+1)(m+n 1)
=[n (m 1)][n+ (m 1)]
=n2 (m 1)2
=n2 (m2 2m+1)
=n2 m2+2m 1
(3) (x y m+n)(x y+m n)
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
2.运用乘法公式计算:
(1) ( m+n+1)(m+n 1) (2) (a 2b 1)2
解: (2) (a 2b 1)2
=[(a 2b) 1]2
=(a 2b)2 2(a 2b)+12
=a2 4ab+4b2 2a+4b+1
也可变形为[a (2b+1)]2
(3) (x y m+n)(x y+m n)
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
解:(3) (x y m+n)(x y+m n)
=[(x y) (m n)][(x y)+(m n)]
=(x y)2 (m n)2
=x2 2xy+y2 m2+2mn n2
2.运用乘法公式计算:
(1) ( m+n+1)(m+n 1) (2) (a 2b 1)2
(3) (x y m+n)(x y+m n)
应用新知
巩固新知
随堂练习
探究新知
课堂小结
布置作业
创设情境
3.灵活运用乘法公式计算:
已知(m+n+1)(m+n 1)=63,则m+n= .
解:∵ (m+n+1)(m+n 1)
=(m+n)2 12=63
∴(m+n)2=64
∴m+n= 8
8
注意:
添括号法则:
添
括
号
法
则
巩固新知
课堂小结
应用新知
探究新知
布置作业
添括号时,如果括号前面是正号,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
创设情境
有些整式相乘需要先通过添括号作适当变形,然后再灵活运用乘法公式计算.
布置作业
教科书第111页
练习第2题
第112页
习题14.2第3题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
