人教版八年级数学上册15.2.3《整数指数幂》第1课时 教学课件(共17张PPT)
文档属性
| 名称 | 人教版八年级数学上册15.2.3《整数指数幂》第1课时 教学课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 15:59:57 | ||
图片预览





文档简介
(共17张PPT)
15.2.3 整数指数幂
第1课时
学习目标
1.知道负整数指数幂 (a≠0,n是正整数);
2.掌握整数指数幂的运算性质;
3.通过探索,让学生体会到从特殊到一般的方法是研究数学的一个重要方法;
4.通过学习课堂知识使学生懂得任何事物之间是相互联系的,理论来源于实践,服务于实践,能利用事物之间的类比性解决问题.
整数指数幂
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
(n是正整数)
(1) am·an=am+n
(n是正整数);
(m,n是正整数);
(2) (am)n=amn
( m,n是正整数);
(3) ( ab) n =a n b n
(n是正整数);
(4) am÷an=am – n
(a≠0,m,n是正整数,m>n);
(5)
(6) a0=1
(a≠0).
正整数指数幂的运算性质:
正整数
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
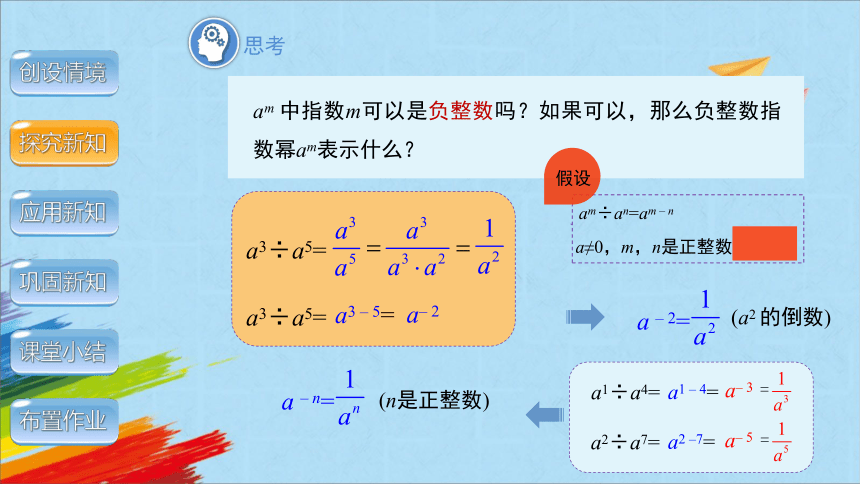
am中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
am÷an=am – n
(a≠0,m,n是正整数,m>n)
a5÷a3=a5 – 3=
a3÷a5=
a5÷a3=
a2
a3÷a5=
3<5
分式的约分
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
am 中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
am÷an=am – n
a≠0,m,n是正整数,m>n.
a3÷a5=
a3÷a5=
a3 – 5=
a– 2
假设
a – 2=
a1÷a4=
a1 – 4=
a– 3
a2÷a7=
a2 –7=
a– 5
a – n=
(a2 的倒数)
(n是正整数)
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
规定:
一般地,当n是正整数时,
归纳
a – n=
(a≠0).
这就是说,a – n是an的倒数.
am÷an=am – n
(a≠0,m,n是正整数,m>n).
(a≠0,m,n是正整数).
可以m>n;
可以m=n;
可以m<n.
负整数指数幂
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
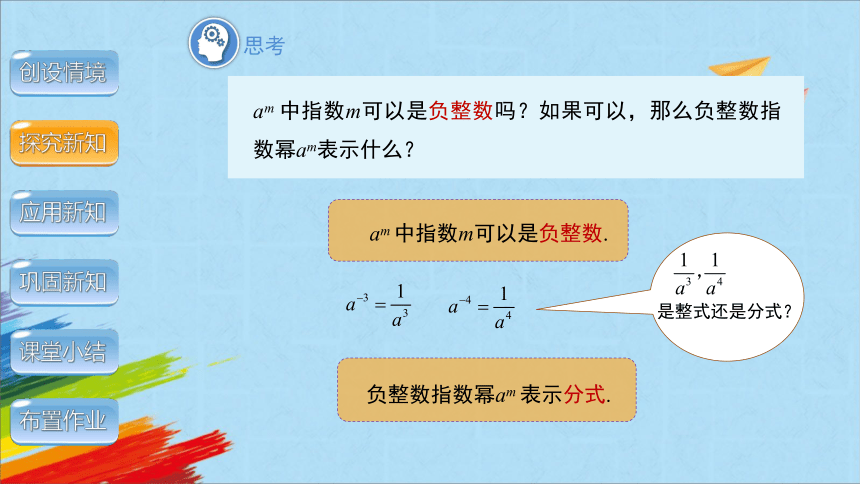
am 中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
am 中指数m可以是负整数.
负整数指数幂am 表示分式.
是整式还是分式?
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
引入负整数指数和0指数后,am·an=am + n (m,n是正整数)这条性质能否推广到m,n是任意整数的情形?
推广到m,n是任意整数的情形?
am·an=am + n
m,n可以是正整数、
负整数、0.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
am·an=am + n这条性质对于m,n是任意整数的情形仍然适用.
归纳
事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂.
(1) am·an=am+n
(2) (am)n=amn
(3) ( ab) n =a n b n
(4) am÷an=am – n
(a≠0 ,m>n)
(5)
(6) a0=1
(a≠0)
(m,n是整数)
(a≠0)
整数指数幂运算性质
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例 计算:
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
下列计算正确的是( )
A.
B.
C.
D.
A
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
计算:
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
计算:
解:原式
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
(★拓展)练习4
随堂练习
计算:
解:原式
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
整数指数幂
规定:
一般地,当n是正整数时,
a – n=
(a≠0).
这就是说,a – n是an的倒数.
(1) am·an=am+n
(2) (am)n=amn
(3) (ab) n =a n b n
(4) am÷an=am – n
(a≠0 )
(5)
整数指数幂的运算性质(m,n是整数)
(6) a0=1
(a≠0)
布置作业
教科书第147页练习7.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
15.2.3 整数指数幂
第1课时
学习目标
1.知道负整数指数幂 (a≠0,n是正整数);
2.掌握整数指数幂的运算性质;
3.通过探索,让学生体会到从特殊到一般的方法是研究数学的一个重要方法;
4.通过学习课堂知识使学生懂得任何事物之间是相互联系的,理论来源于实践,服务于实践,能利用事物之间的类比性解决问题.
整数指数幂
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
(n是正整数)
(1) am·an=am+n
(n是正整数);
(m,n是正整数);
(2) (am)n=amn
( m,n是正整数);
(3) ( ab) n =a n b n
(n是正整数);
(4) am÷an=am – n
(a≠0,m,n是正整数,m>n);
(5)
(6) a0=1
(a≠0).
正整数指数幂的运算性质:
正整数
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
am中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
am÷an=am – n
(a≠0,m,n是正整数,m>n)
a5÷a3=a5 – 3=
a3÷a5=
a5÷a3=
a2
a3÷a5=
3<5
分式的约分
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
am 中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
am÷an=am – n
a≠0,m,n是正整数,m>n.
a3÷a5=
a3÷a5=
a3 – 5=
a– 2
假设
a – 2=
a1÷a4=
a1 – 4=
a– 3
a2÷a7=
a2 –7=
a– 5
a – n=
(a2 的倒数)
(n是正整数)
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
规定:
一般地,当n是正整数时,
归纳
a – n=
(a≠0).
这就是说,a – n是an的倒数.
am÷an=am – n
(a≠0,m,n是正整数,m>n).
(a≠0,m,n是正整数).
可以m>n;
可以m=n;
可以m<n.
负整数指数幂
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
am 中指数m可以是负整数吗?如果可以,那么负整数指数幂am表示什么?
am 中指数m可以是负整数.
负整数指数幂am 表示分式.
是整式还是分式?
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
引入负整数指数和0指数后,am·an=am + n (m,n是正整数)这条性质能否推广到m,n是任意整数的情形?
推广到m,n是任意整数的情形?
am·an=am + n
m,n可以是正整数、
负整数、0.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
am·an=am + n这条性质对于m,n是任意整数的情形仍然适用.
归纳
事实上,随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂.
(1) am·an=am+n
(2) (am)n=amn
(3) ( ab) n =a n b n
(4) am÷an=am – n
(a≠0 ,m>n)
(5)
(6) a0=1
(a≠0)
(m,n是整数)
(a≠0)
整数指数幂运算性质
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
例 计算:
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
下列计算正确的是( )
A.
B.
C.
D.
A
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
计算:
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习3
随堂练习
计算:
解:原式
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
(★拓展)练习4
随堂练习
计算:
解:原式
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
整数指数幂
规定:
一般地,当n是正整数时,
a – n=
(a≠0).
这就是说,a – n是an的倒数.
(1) am·an=am+n
(2) (am)n=amn
(3) (ab) n =a n b n
(4) am÷an=am – n
(a≠0 )
(5)
整数指数幂的运算性质(m,n是整数)
(6) a0=1
(a≠0)
布置作业
教科书第147页练习7.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
