人教版八年级数学上册>15.2.3《整数指数幂》第2课时教学课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册>15.2.3《整数指数幂》第2课时教学课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-26 16:45:46 | ||
图片预览








文档简介
(共20张PPT)
15.2.3 整数指数幂
第2课时
学习目标
1.了解科学记数法,会用科学记数法表示绝对值小于1的数;
2. 能够理解科学记数法中的指数与小数点后面零的个数的关系;
3.经历将10的负整数幂与数互化的过程,体会数学知识间的相互联系;
4.通过体会数的多种表达形式,使学生感受到数学知识来源于生活,用于使生活更方便,提升学生对数学的热爱.
用科学记数法表示
绝对值较小的数
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
(1)864 000= ;
(2) – 135 200= .
已学过科学记数法,利用10的正整数次幂,把一个绝对值大于10的数表示成a×10n的形式,其中n是正整数,1≤|a|<10.
8.64×105
– 1.352×105
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
一些较大的数适合用科学记数法表示.
光速约为3×108 m/s
2010年世界人数约为 6.9×109
太阳半径约为6.96×105 km
有了负整数指数幂后,小于1的正数也可以用科学记数法表示.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
小于1的正数可以用科学记数法表示为a×10–n的形式,其中1≤∣a∣<10,n是正整数.
归纳
例如:
0.00001= 10–5
0.0000257= 2.57×10–5
0.0000000257= 2.57×10–8
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
0.000 000 0035=3.5×10 ?
0.000 000 00107=1.07×10 ?
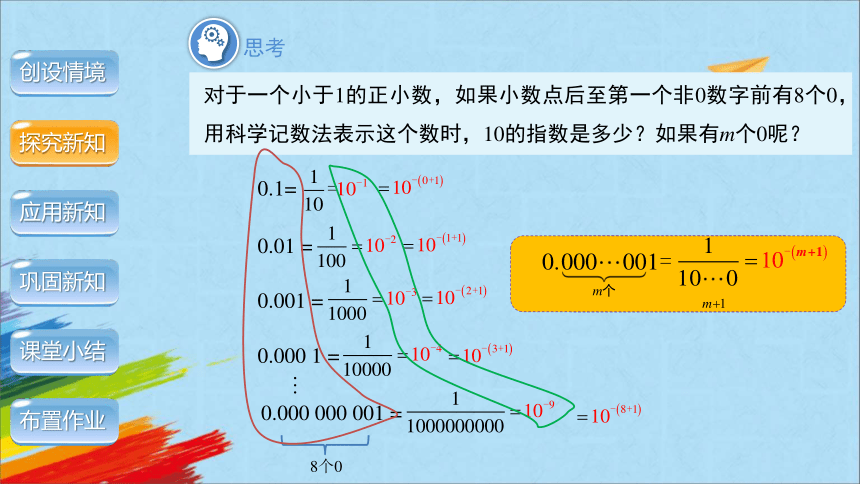
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
=3.5×10 ?
观察小数点后至第一个非0数字前0的个数与指数关系.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
0.1=
0.001 =
0.01 =
0.000 1 =
0.000 000 001 =
…
8个0
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
0.000 000 0035=3.5×10 ?
0.000 000 00107=1.07×10 ?
8个0
3.5×10–9
1.07×10–9
–9
3.5×0.000 000 001=
1.07×0.000 000 001=
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是–9.如果有m个0呢?
对于一个小于1的正小数,如果小数点后至第一个非0数字前有m个0,用科学记数法表示这个数时,10的指数– (m+1).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
对于一个小于1的正小数,如果小数点后至第一个非0数字前有m个0,用科学记数法表示这个数时,10的指数– (m+1).
用科学记数法表示小于1的正数的一般步骤:
(1) 确定a:a是大于或等于1且小于10的数;
(2) 确定n:小数点后至第一个非0数字前,0的个数加1为n.
将原数用科学记数法表示为a×10–n(其中1≤a<10,n是正整数).
做一做
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
用科学记数法表示下列数:
0.000 000 001=
0.0012=
0.000 000 345=
0.000 000 010 8=
0.000 01=
0.000 02=
0.000 000 567=
0.000 000 301=
1×10–9
1.2×10–3
3.45×10–7
1.08×10–8
1×10–5
2×10–5
5.67×10–7
3.01×10–7
绝对值小于1的数都可以用科学记数法表示成 a×10–n 的形式(其中1≤∣a∣<10,n是正整数).
– 0.000072=
7.2×10–5
先用科学记数法表示出绝对值的,再添加“–”.
–
做一做
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
解:(1) 6×10–4 =0.0006;
(2) –7.2×10–5 = –0.000072;
(3) 5.68×10–6 =0.00000568.
将下列用科学记数法表示的数还原.
(1) 6×10–4 ; (2) –7.2×10–5 ; (3) 5.68×10–6 .
a×10–n 的形式(其中1≤∣a∣<10,n是正整数),还原成原数,即a中的小数点向左挪动n位.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
纳米(nm)是非常小的长度单位,1 nm =10–9 m,把1 nm3的物体放在兵乓球上,就如同把乒乓球放在地球上.1 mm3的空间可以放多少个1 nm3的物体(物体之间的间隙忽略不计)?
解:1 mm=10–3 m,1 nm =10–9 m.
(10–3)3÷(10–9)3=10–9÷10–27=10–9– (–27)=1018 .
1 mm3的空间可以放1018 个1 nm3的物体.
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
2020年6月23日9时43分,我国成功发射了北斗系统第55颗导航卫星,其授时精度为世界之最,不超过0.0000000099秒.数据“0.0000000099”用科学记数法表示为( )
A. 99×10–10 B. 9.9×10–10
C. 9.9×10–9 D. 0.99×10–8
从小数点后,第一个非0数前有8个0.
C
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
用科学记数法表示的数的计算:
(1) ; (2) .
先计算乘方,再计算乘除,最后将结果用科学记数法表示.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
解:(1)
最终结果要用科学记数法表示.
用科学记数法表示的数的计算:
(1) ; (2) .
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
用科学记数法表示的数的计算:
(1) ; (2) .
解:(2)
用科学记数法表示的数是一个整体,要用括号括起来.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
用科学记数法表示绝对值较小的数
(6) a0=1
(a≠0)
小于1的正数可以用科学记数法表示为a×10–n的形式,其中1≤∣a∣<10,n是正整数.
用科学记数法表示小于1的正数的一般步骤:
(1) 确定a:a是大于或等于1且小于10的数;
(2) 确定n:小数点后至第一个非0数字前,0的个数加1为n.
将原数用科学记数法表示为a×10–n(其中1≤a<10,n是正整数).
布置作业
教科书第146页8题、9题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
15.2.3 整数指数幂
第2课时
学习目标
1.了解科学记数法,会用科学记数法表示绝对值小于1的数;
2. 能够理解科学记数法中的指数与小数点后面零的个数的关系;
3.经历将10的负整数幂与数互化的过程,体会数学知识间的相互联系;
4.通过体会数的多种表达形式,使学生感受到数学知识来源于生活,用于使生活更方便,提升学生对数学的热爱.
用科学记数法表示
绝对值较小的数
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
(1)864 000= ;
(2) – 135 200= .
已学过科学记数法,利用10的正整数次幂,把一个绝对值大于10的数表示成a×10n的形式,其中n是正整数,1≤|a|<10.
8.64×105
– 1.352×105
回顾
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
一些较大的数适合用科学记数法表示.
光速约为3×108 m/s
2010年世界人数约为 6.9×109
太阳半径约为6.96×105 km
有了负整数指数幂后,小于1的正数也可以用科学记数法表示.
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
小于1的正数可以用科学记数法表示为a×10–n的形式,其中1≤∣a∣<10,n是正整数.
归纳
例如:
0.00001= 10–5
0.0000257= 2.57×10–5
0.0000000257= 2.57×10–8
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
思考
0.000 000 0035=3.5×10 ?
0.000 000 00107=1.07×10 ?
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
=3.5×10 ?
观察小数点后至第一个非0数字前0的个数与指数关系.
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
0.1=
0.001 =
0.01 =
0.000 1 =
0.000 000 001 =
…
8个0
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少?如果有m个0呢?
0.000 000 0035=3.5×10 ?
0.000 000 00107=1.07×10 ?
8个0
3.5×10–9
1.07×10–9
–9
3.5×0.000 000 001=
1.07×0.000 000 001=
思考
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是–9.如果有m个0呢?
对于一个小于1的正小数,如果小数点后至第一个非0数字前有m个0,用科学记数法表示这个数时,10的指数– (m+1).
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
对于一个小于1的正小数,如果小数点后至第一个非0数字前有m个0,用科学记数法表示这个数时,10的指数– (m+1).
用科学记数法表示小于1的正数的一般步骤:
(1) 确定a:a是大于或等于1且小于10的数;
(2) 确定n:小数点后至第一个非0数字前,0的个数加1为n.
将原数用科学记数法表示为a×10–n(其中1≤a<10,n是正整数).
做一做
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
用科学记数法表示下列数:
0.000 000 001=
0.0012=
0.000 000 345=
0.000 000 010 8=
0.000 01=
0.000 02=
0.000 000 567=
0.000 000 301=
1×10–9
1.2×10–3
3.45×10–7
1.08×10–8
1×10–5
2×10–5
5.67×10–7
3.01×10–7
绝对值小于1的数都可以用科学记数法表示成 a×10–n 的形式(其中1≤∣a∣<10,n是正整数).
– 0.000072=
7.2×10–5
先用科学记数法表示出绝对值的,再添加“–”.
–
做一做
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
解:(1) 6×10–4 =0.0006;
(2) –7.2×10–5 = –0.000072;
(3) 5.68×10–6 =0.00000568.
将下列用科学记数法表示的数还原.
(1) 6×10–4 ; (2) –7.2×10–5 ; (3) 5.68×10–6 .
a×10–n 的形式(其中1≤∣a∣<10,n是正整数),还原成原数,即a中的小数点向左挪动n位.
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
典型例题
纳米(nm)是非常小的长度单位,1 nm =10–9 m,把1 nm3的物体放在兵乓球上,就如同把乒乓球放在地球上.1 mm3的空间可以放多少个1 nm3的物体(物体之间的间隙忽略不计)?
解:1 mm=10–3 m,1 nm =10–9 m.
(10–3)3÷(10–9)3=10–9÷10–27=10–9– (–27)=1018 .
1 mm3的空间可以放1018 个1 nm3的物体.
1018是一个非常大的数,它是1亿(即108)的100亿(即1010)倍.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习1
随堂练习
2020年6月23日9时43分,我国成功发射了北斗系统第55颗导航卫星,其授时精度为世界之最,不超过0.0000000099秒.数据“0.0000000099”用科学记数法表示为( )
A. 99×10–10 B. 9.9×10–10
C. 9.9×10–9 D. 0.99×10–8
从小数点后,第一个非0数前有8个0.
C
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
用科学记数法表示的数的计算:
(1) ; (2) .
先计算乘方,再计算乘除,最后将结果用科学记数法表示.
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
解:(1)
最终结果要用科学记数法表示.
用科学记数法表示的数的计算:
(1) ; (2) .
课堂小结
布置作业
创设情境
探究新知
应用新知
巩固新知
练习2
随堂练习
用科学记数法表示的数的计算:
(1) ; (2) .
解:(2)
用科学记数法表示的数是一个整体,要用括号括起来.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
用科学记数法表示绝对值较小的数
(6) a0=1
(a≠0)
小于1的正数可以用科学记数法表示为a×10–n的形式,其中1≤∣a∣<10,n是正整数.
用科学记数法表示小于1的正数的一般步骤:
(1) 确定a:a是大于或等于1且小于10的数;
(2) 确定n:小数点后至第一个非0数字前,0的个数加1为n.
将原数用科学记数法表示为a×10–n(其中1≤a<10,n是正整数).
布置作业
教科书第146页8题、9题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
