全等三角形条件(3)[上学期]
文档属性
| 名称 | 全等三角形条件(3)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 420.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-24 16:51:00 | ||
图片预览



文档简介
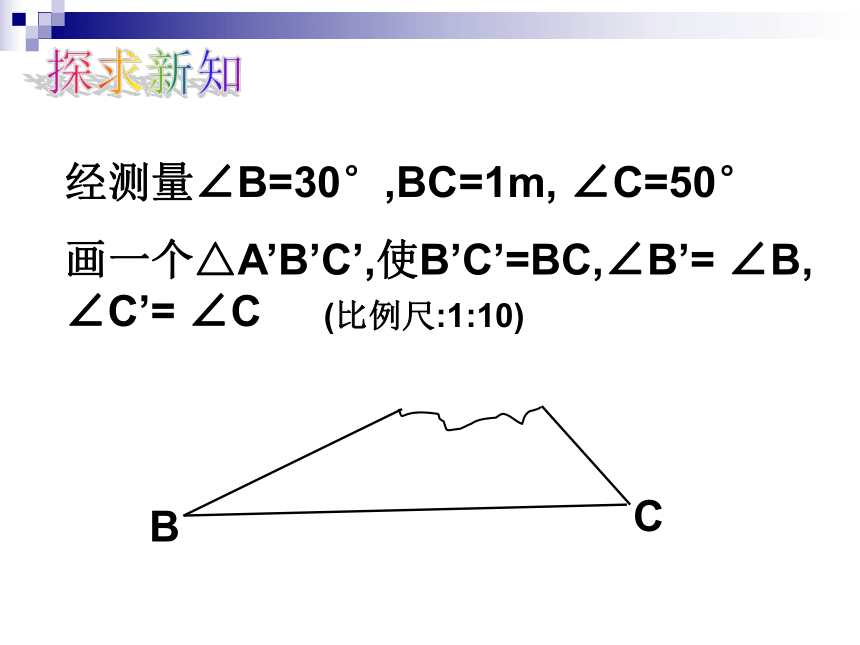
课件15张PPT。全等三角形的条件(3)临海外国语学校何华龙帮帮我 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?(2)(1)探求新知经测量∠B=30°,BC=1m, ∠C=50°
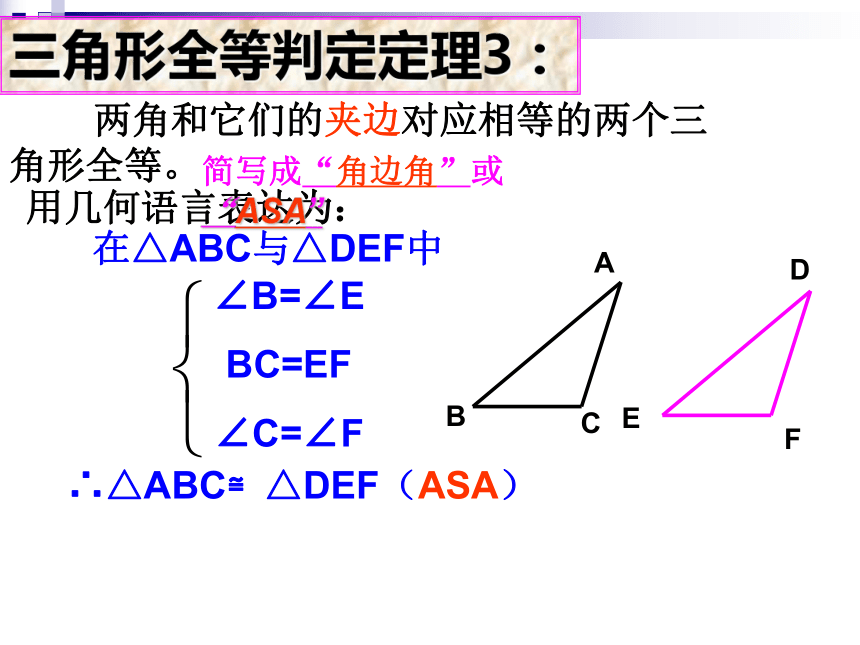
画一个△A’B’C’,使B’C’=BC,∠B’= ∠B, ∠C’= ∠C(比例尺:1:10)三角形全等判定定理3:用几何语言表达为:在△ABC与△DEF中∠B=∠E
BC=EF
∠C=∠F
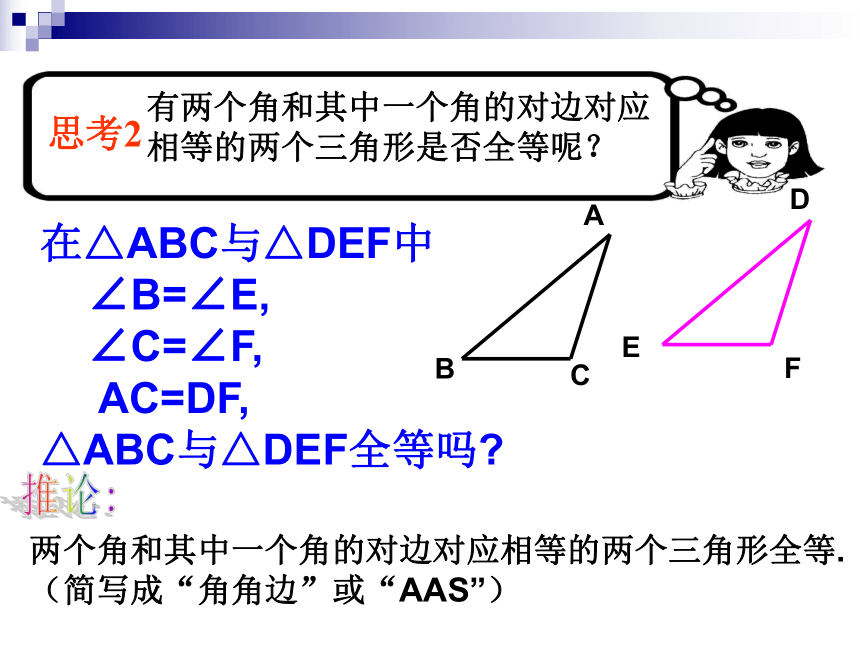
∴△ABC≌△DEF(ASA) 两角和它们的夹边对应相等的两个三角形全等。简写成“角边角”或 “ASA”在△ABC与△DEF中
∠B=∠E,
∠C=∠F,
AC=DF,
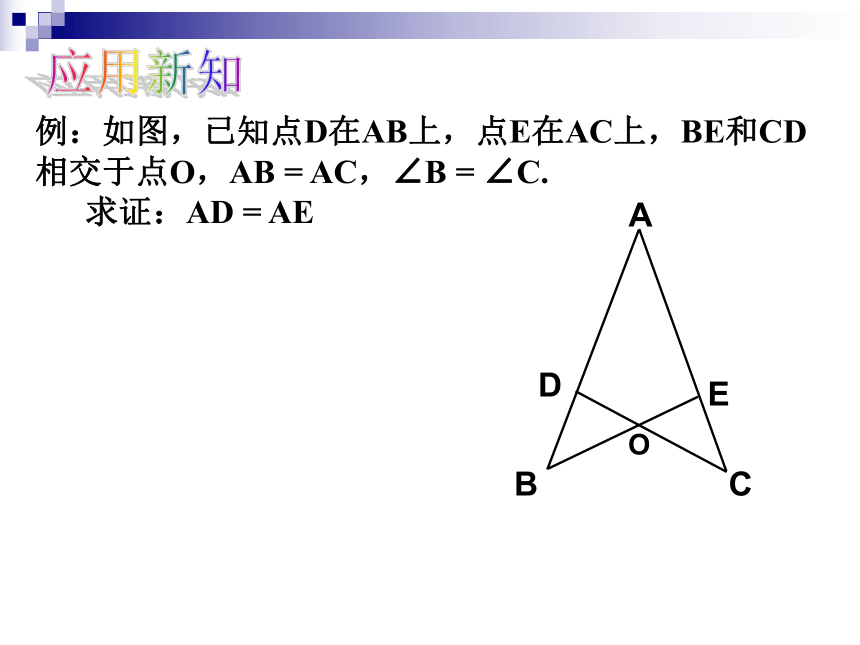
△ABC与△DEF全等吗?三角对应相等的两个三角形全等吗?考考你:应用新知例:如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB = AC,∠B = ∠C.
求证:AD = AE练一练 1.如图:要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么?2.如图,AB⊥BC,AD ⊥DC,∠1=∠2.
求证: AB=AD练一练1 请同学们利用两个全等三角形拼出多种基本图形.动一动(1)(2)(9)(8)(7)(6)(5)(4)(3)(11)(10)拓展新知请添加两个条件 ,
使得△ABD≌△CDB. 拓展新知请添加 条件
使得△ABE≌△ACD. 图中共有几对全等三角形?课堂小结1、这节课你学会了什么方法判定两个三角形全等?2、到目前为止,共有几种方法判定两个三角形全等?3、全等三角形在几何证明中有何应用?4、在几何证明过程中要充分利用好基本图形。作业1.作业本(1)
2.拓展:已知∠A=∠D,∠ABC=∠DCB,
求证:OA=OD
画一个△A’B’C’,使B’C’=BC,∠B’= ∠B, ∠C’= ∠C(比例尺:1:10)三角形全等判定定理3:用几何语言表达为:在△ABC与△DEF中∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA) 两角和它们的夹边对应相等的两个三角形全等。简写成“角边角”或 “ASA”在△ABC与△DEF中
∠B=∠E,
∠C=∠F,
AC=DF,
△ABC与△DEF全等吗?三角对应相等的两个三角形全等吗?考考你:应用新知例:如图,已知点D在AB上,点E在AC上,BE和CD相交于点O,AB = AC,∠B = ∠C.
求证:AD = AE练一练 1.如图:要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么?2.如图,AB⊥BC,AD ⊥DC,∠1=∠2.
求证: AB=AD练一练1 请同学们利用两个全等三角形拼出多种基本图形.动一动(1)(2)(9)(8)(7)(6)(5)(4)(3)(11)(10)拓展新知请添加两个条件 ,
使得△ABD≌△CDB. 拓展新知请添加 条件
使得△ABE≌△ACD. 图中共有几对全等三角形?课堂小结1、这节课你学会了什么方法判定两个三角形全等?2、到目前为止,共有几种方法判定两个三角形全等?3、全等三角形在几何证明中有何应用?4、在几何证明过程中要充分利用好基本图形。作业1.作业本(1)
2.拓展:已知∠A=∠D,∠ABC=∠DCB,
求证:OA=OD
