第十三章 全等三角形(复习)[上学期]
文档属性
| 名称 | 第十三章 全等三角形(复习)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 72.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-27 20:17:00 | ||
图片预览




文档简介
课件13张PPT。第十三章 全等三角形(复习)1、如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )乙、丙从反面找一相等的边或角进行排除;用全等判定方法识别两三角形全等;2、下列说法错误的是( )
A、两条直角边对应相等的两个直角三角形全等;
B、斜边和一条直角边对应相等的两个直角三角形全等;
C、两个锐角对应相等的两个直角三角形全等;
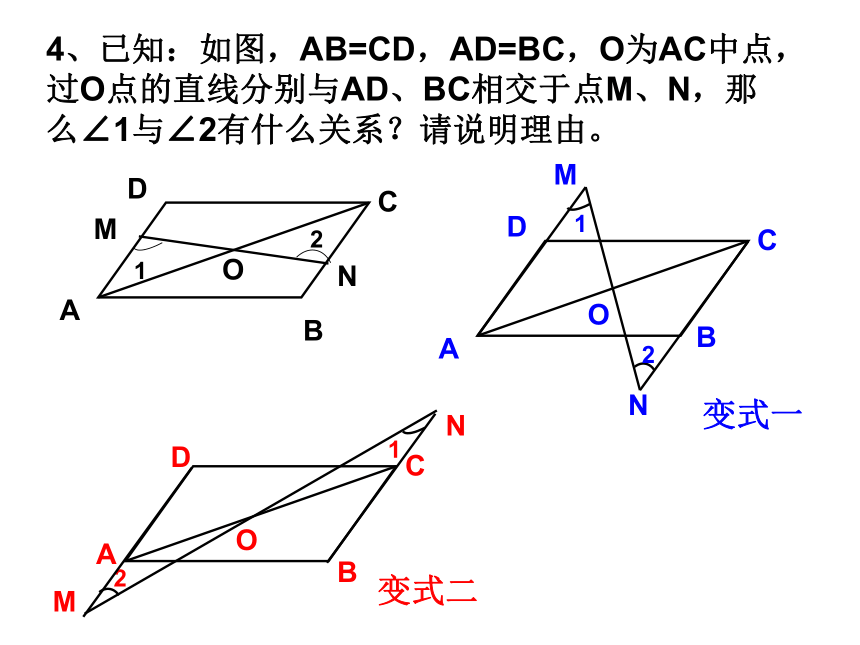
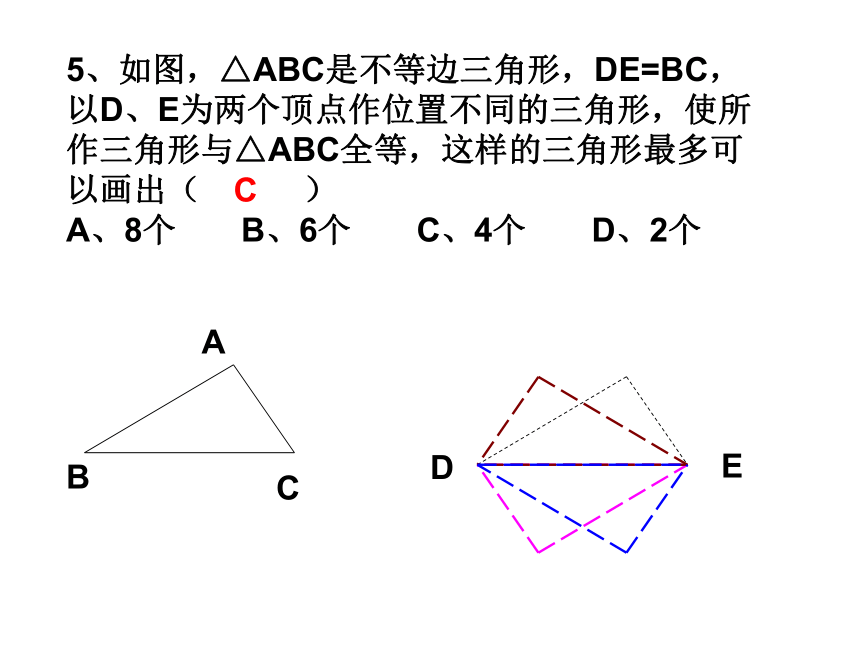
D、一边一锐角对应相等的两个直角三角形全等;C3、根据下列已知条件,能判断△ABC≌△A?B?C?的是( )A、AB=A ? B ? BC=B ? C ? ∠A= ∠A ?B、∠A= ∠A ? ∠C= ∠C ? AC=B ? C ?C、∠A= ∠A ? ∠B= ∠B ? ∠C= ∠C ? D、AB=A?B ? BC=B ? C ? △ABC的周长等于△A?B?C?的周长。D4、已知:如图,AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由。变式二变式一5、如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )
A、8个 B、6个 C、4个 D、2个ABCDEC6、如图,∠ACB=90o,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm。
求:BE的长。7、在△ABC中,∠B= ∠C,与△ABC全等的三角形中有一个角为100o,那么△ABC中与这个角对应的角的( )
A、∠A B、 ∠B
C、∠C D、不能确定A8、如图,四边形ABCD中,AC平分∠DAB,若AB>AD,DC=BC,
求证:∠B+ ∠D=180oE添辅助线构造全等三角形;9、如图,△ABC中,∠ACB=2∠B,∠1=∠2,试说明:AB=AC+CDABCD12EF证明一条线段等于另两条线段之和,常用的方法是:“补短法”;“截长法”。
补短法:延长一条短线段使其等于长线段,再证明延长部分与另一短线段相等;
截长法:在长线段上截取一条线段等于短线段,再证明余下部分与另一条短线段相等。10.如图,在△ABC中,AB=12,AC=8,AD是BC边上
的中线,求AD的取值范围.特别提示:
把三角形的一边的中线加倍延长,把分散条件集中
到同一个三角形中是解决中线问题的基本规律.添辅助线构造全等三角形解题11.若AD是Rt△ABC的斜边上的中线,那么△ABD≌△ADC吗?
为什么?
小明是这样想的:
△ABD≌△ADC 这是因为:
△ABC为直角三角形. △ABD≌△ADC 小明思考得对吗? 拓展与延伸下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
A、两条直角边对应相等的两个直角三角形全等;
B、斜边和一条直角边对应相等的两个直角三角形全等;
C、两个锐角对应相等的两个直角三角形全等;
D、一边一锐角对应相等的两个直角三角形全等;C3、根据下列已知条件,能判断△ABC≌△A?B?C?的是( )A、AB=A ? B ? BC=B ? C ? ∠A= ∠A ?B、∠A= ∠A ? ∠C= ∠C ? AC=B ? C ?C、∠A= ∠A ? ∠B= ∠B ? ∠C= ∠C ? D、AB=A?B ? BC=B ? C ? △ABC的周长等于△A?B?C?的周长。D4、已知:如图,AB=CD,AD=BC,O为AC中点,过O点的直线分别与AD、BC相交于点M、N,那么∠1与∠2有什么关系?请说明理由。变式二变式一5、如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )
A、8个 B、6个 C、4个 D、2个ABCDEC6、如图,∠ACB=90o,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm。
求:BE的长。7、在△ABC中,∠B= ∠C,与△ABC全等的三角形中有一个角为100o,那么△ABC中与这个角对应的角的( )
A、∠A B、 ∠B
C、∠C D、不能确定A8、如图,四边形ABCD中,AC平分∠DAB,若AB>AD,DC=BC,
求证:∠B+ ∠D=180oE添辅助线构造全等三角形;9、如图,△ABC中,∠ACB=2∠B,∠1=∠2,试说明:AB=AC+CDABCD12EF证明一条线段等于另两条线段之和,常用的方法是:“补短法”;“截长法”。
补短法:延长一条短线段使其等于长线段,再证明延长部分与另一短线段相等;
截长法:在长线段上截取一条线段等于短线段,再证明余下部分与另一条短线段相等。10.如图,在△ABC中,AB=12,AC=8,AD是BC边上
的中线,求AD的取值范围.特别提示:
把三角形的一边的中线加倍延长,把分散条件集中
到同一个三角形中是解决中线问题的基本规律.添辅助线构造全等三角形解题11.若AD是Rt△ABC的斜边上的中线,那么△ABD≌△ADC吗?
为什么?
小明是这样想的:
△ABD≌△ADC 这是因为:
△ABC为直角三角形. △ABD≌△ADC 小明思考得对吗? 拓展与延伸下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
