全等三角形的复习[上学期]
文档属性
| 名称 | 全等三角形的复习[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 403.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-27 00:00:00 | ||
图片预览


文档简介
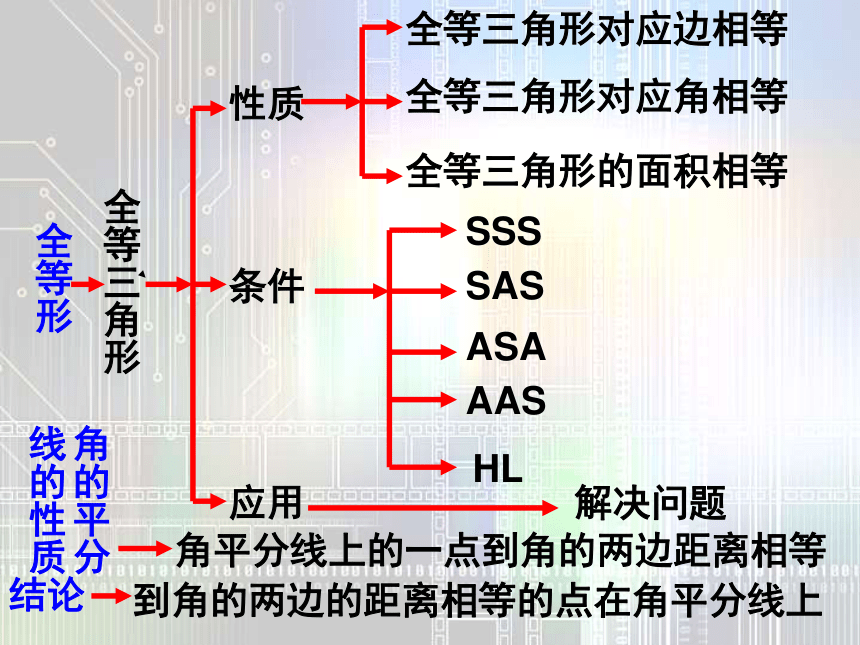
课件16张PPT。全等三角形的复习八年级数学第十三章全等形全等三角形性质条件应用全等三角形对应边相等全等三角形对应角相等全等三角形的面积相等SSSSASASAAASHL解决问题角的平分线的性质角平分线上的一点到角的两边距离相等
到角的两边的距离相等的点在角平分线上结论全等三角形
⑷证明两个三角形全等,要结合题目的条件和结论,选择恰当方法
⑸全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
④设法证明所缺的条件,有时所缺的条件可能在另一对全等三角形中,必须证两次全等。
⑤当要证的相等线段或角分别在两组以上的可能全等的三角形中,就应分析证明哪对三角形全等最好,一般选择条件具备多的一对较简单。
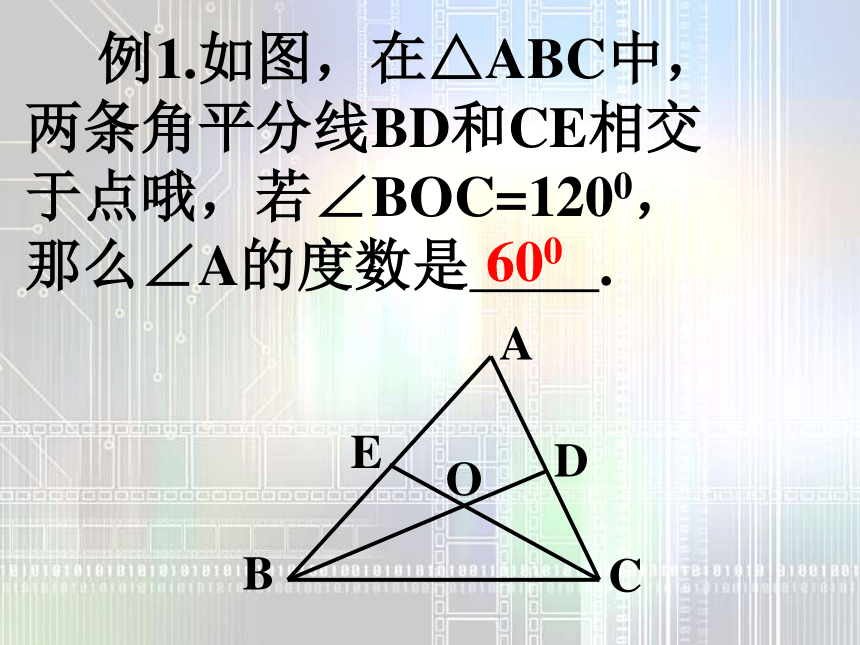
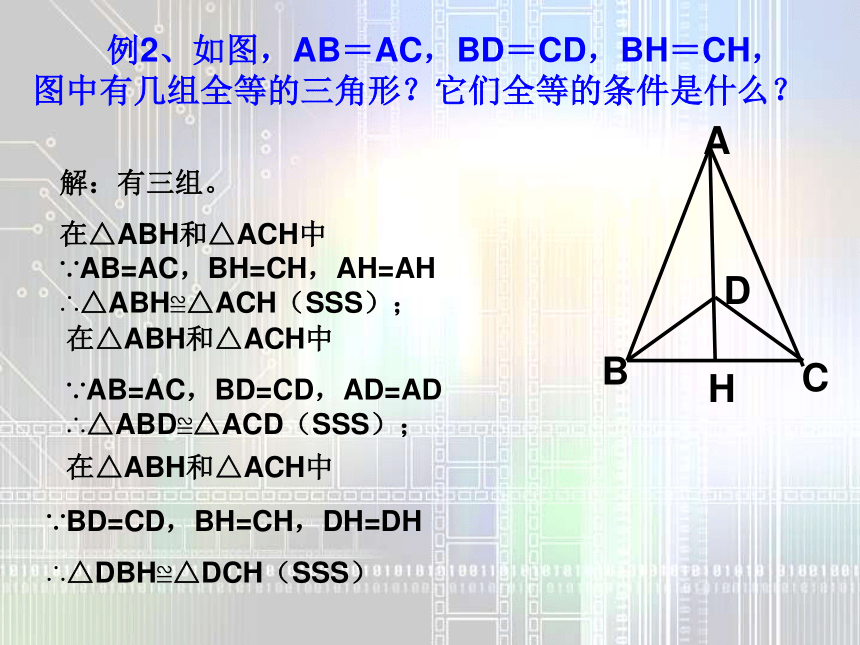
⑹有时证两线段相等,如存在角平分线且存在角平分线上的点到角的两边的垂线段就可直接用角平分线的性质定理来证,而不要去证三角形全等。 总之,证明过程中能用简单方法的就不要绕弯路。 例1.如图,在△ABC中,两条角平分线BD和CE相交于点哦,若∠BOC=1200,那么∠A的度数是 .600 例2、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。
在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS) 在△ABH和△ACH中
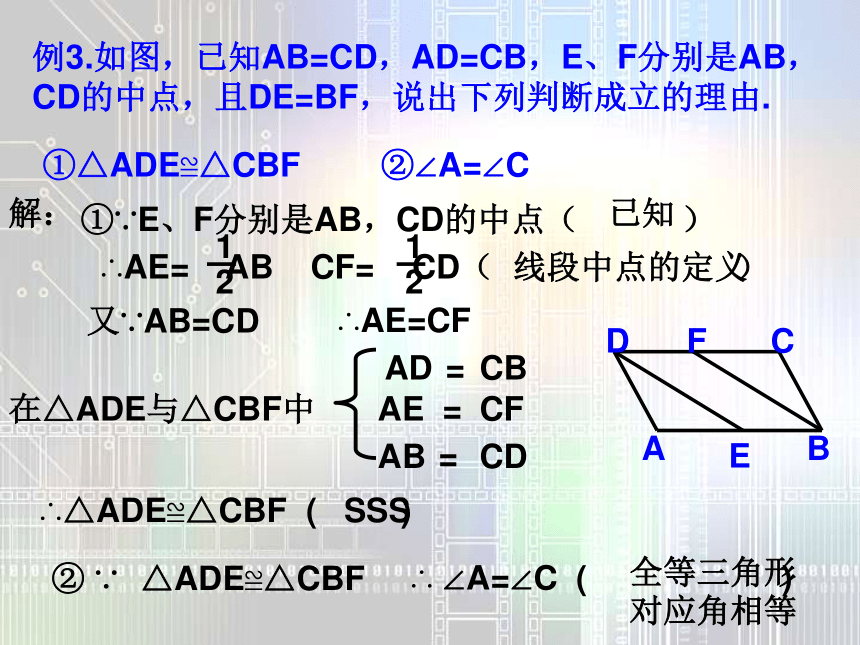
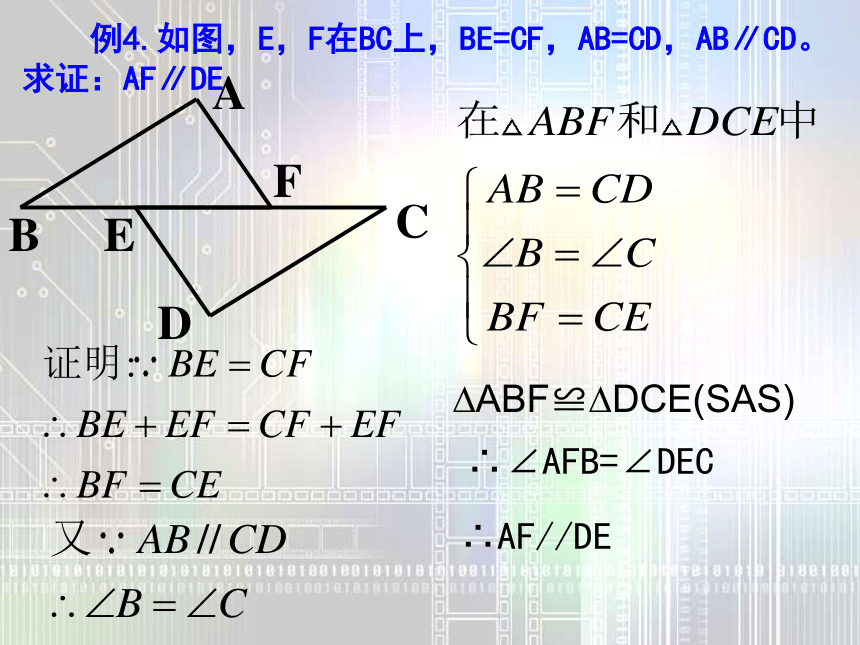
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中解:①∵E、F分别是AB,CD的中点( )又∵AB=CD∴AE=CF在△ADE与△CBF中AE ==∴△ADE≌△CBF ( )∴AE= AB CF= CD( )例3.如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠C线段中点的定义CFADABCDSSS△ADE≌△CBF全等三角形对应角相等已知CB② ∵∴ ∠A=∠C ( )= 例4.如图,E,F在BC上,BE=CF,AB=CD,AB∥CD。求证:AF∥DE?ABF≌?DCE(SAS)∴∠AFB=∠DEC∴AF//DE∵ AB∥CD,AD∥BC(已知 )∴ ∠1=∠2 ∠3=∠4
在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)∴ △ABC≌△CDA(ASA)∴ AB=CD BC=AD(全等三角形对应边相等)证明:连结AC.例5.如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?ABCD2341 例6.如图,已知AB=AD, ∠B=∠D,∠1=∠2,
求证:BC=DE证明:∵∠1=∠2∴∠1+∠EAC=∠2+∠EAC∴∠BAC=∠DAE在?ABC和?ADE中∴?ABC≌?ADE(AAS)∴BC=DE解∵ CE ⊥ AB,DF⊥ AC(已知)
∴ ∠ AEC= ∠ BFD=Rt∠
∵ AF=BE (已知)
即AE+EF=BF+EF
AE=BF
∵ AC=BD
∴ RtΔACE ≌ RtΔBDF(HL)
∴ CE=DF(全等三角形的对应边相等)ABCDEF 例7. 如图,已知CE ⊥AB,DF ⊥ AB,AC=BD,AF=BE,则CE=DF。请说明理由。 例8.已知:∠ACB=∠ADB=900,AC=AD,P是AB上任意一点,求证:CP=DP
证明:在Rt?ABC和Rt?ABD中∴Rt?ABC≌Rt?ABD∴∠CAB=∠DAB∴?APC≌?APD(SAS)∴CP=DP 例9. 如图CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点O,且∠1=∠2,求证OB=OC。 证明:∵∠1=∠2 CD⊥AB,BE⊥AC ∴OD=OE(角平分线的性质定理) 在△OBD与△OCE中 ∴△OBD≌△OCE(ASA) ∴OB=OC 例10. 如图A、B、C在一直线上,△ABD,△BCE都是等边三角形,AE交BD于F,DC交BE于G,求证:BF=BG。 证明:∵△ABD,△BCE是等边三角形。 ∴∠DBA=△EBC=60°
∵ A、B、C共线∴∠DBE=60° ∴∠ABE=∠DBC 在△ABE与△DBC中 ∴△ABE≌△DBC(SAS) ∴∠2=∠1 在△BEF与△BCG中 ∴△BEF≌△BCG(ASA) ∴BF=BG(全等三角形对应边相等)例11.如图AB//CD,∠B=90o,E是BC的中点,DE平分
∠ADC,求证:AE平分∠DABCDBAEF证明:作EF⊥AD,垂足为F
∵DE平分∠ADC
AB//CD,∴∠C=∠B
又∵∠B=90o∴∠C=90o又∵EF⊥AD
∴EF=CE
又∵E是BC的中点
∴EB=EC
∴EF=EB
∵∠B=90o
∴EB⊥AB
∴AE平分∠DAB∴BC⊥DC 例12. 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。∵AB=AC(已知)
AD=AD(公共边)∴Rt△ABD≌Rt△ACD(HL)∴BD=CD解:BD=CD∵ ∠ADB=∠ADC=90°同学们,再见!
⑸全等三角形,是证明两条线段或两个角相等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三角形中。
②分析要证两个三角形全等,已有什么条件,还缺什么条件。
③有公共边的,公共边一定是对应边, 有公共角的,公共角一定是对应角,有对顶角,对顶角也是对应角
④设法证明所缺的条件,有时所缺的条件可能在另一对全等三角形中,必须证两次全等。
⑤当要证的相等线段或角分别在两组以上的可能全等的三角形中,就应分析证明哪对三角形全等最好,一般选择条件具备多的一对较简单。
⑹有时证两线段相等,如存在角平分线且存在角平分线上的点到角的两边的垂线段就可直接用角平分线的性质定理来证,而不要去证三角形全等。 总之,证明过程中能用简单方法的就不要绕弯路。 例1.如图,在△ABC中,两条角平分线BD和CE相交于点哦,若∠BOC=1200,那么∠A的度数是 .600 例2、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。
在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS) 在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中解:①∵E、F分别是AB,CD的中点( )又∵AB=CD∴AE=CF在△ADE与△CBF中AE ==∴△ADE≌△CBF ( )∴AE= AB CF= CD( )例3.如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.①△ADE≌△CBF②∠A=∠C线段中点的定义CFADABCDSSS△ADE≌△CBF全等三角形对应角相等已知CB② ∵∴ ∠A=∠C ( )= 例4.如图,E,F在BC上,BE=CF,AB=CD,AB∥CD。求证:AF∥DE?ABF≌?DCE(SAS)∴∠AFB=∠DEC∴AF//DE∵ AB∥CD,AD∥BC(已知 )∴ ∠1=∠2 ∠3=∠4
在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)∴ △ABC≌△CDA(ASA)∴ AB=CD BC=AD(全等三角形对应边相等)证明:连结AC.例5.如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?ABCD2341 例6.如图,已知AB=AD, ∠B=∠D,∠1=∠2,
求证:BC=DE证明:∵∠1=∠2∴∠1+∠EAC=∠2+∠EAC∴∠BAC=∠DAE在?ABC和?ADE中∴?ABC≌?ADE(AAS)∴BC=DE解∵ CE ⊥ AB,DF⊥ AC(已知)
∴ ∠ AEC= ∠ BFD=Rt∠
∵ AF=BE (已知)
即AE+EF=BF+EF
AE=BF
∵ AC=BD
∴ RtΔACE ≌ RtΔBDF(HL)
∴ CE=DF(全等三角形的对应边相等)ABCDEF 例7. 如图,已知CE ⊥AB,DF ⊥ AB,AC=BD,AF=BE,则CE=DF。请说明理由。 例8.已知:∠ACB=∠ADB=900,AC=AD,P是AB上任意一点,求证:CP=DP
证明:在Rt?ABC和Rt?ABD中∴Rt?ABC≌Rt?ABD∴∠CAB=∠DAB∴?APC≌?APD(SAS)∴CP=DP 例9. 如图CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点O,且∠1=∠2,求证OB=OC。 证明:∵∠1=∠2 CD⊥AB,BE⊥AC ∴OD=OE(角平分线的性质定理) 在△OBD与△OCE中 ∴△OBD≌△OCE(ASA) ∴OB=OC 例10. 如图A、B、C在一直线上,△ABD,△BCE都是等边三角形,AE交BD于F,DC交BE于G,求证:BF=BG。 证明:∵△ABD,△BCE是等边三角形。 ∴∠DBA=△EBC=60°
∵ A、B、C共线∴∠DBE=60° ∴∠ABE=∠DBC 在△ABE与△DBC中 ∴△ABE≌△DBC(SAS) ∴∠2=∠1 在△BEF与△BCG中 ∴△BEF≌△BCG(ASA) ∴BF=BG(全等三角形对应边相等)例11.如图AB//CD,∠B=90o,E是BC的中点,DE平分
∠ADC,求证:AE平分∠DABCDBAEF证明:作EF⊥AD,垂足为F
∵DE平分∠ADC
AB//CD,∴∠C=∠B
又∵∠B=90o∴∠C=90o又∵EF⊥AD
∴EF=CE
又∵E是BC的中点
∴EB=EC
∴EF=EB
∵∠B=90o
∴EB⊥AB
∴AE平分∠DAB∴BC⊥DC 例12. 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。∵AB=AC(已知)
AD=AD(公共边)∴Rt△ABD≌Rt△ACD(HL)∴BD=CD解:BD=CD∵ ∠ADB=∠ADC=90°同学们,再见!
