13.2直角三角形全等的判定 (HL)
文档属性
| 名称 | 13.2直角三角形全等的判定 (HL) |  | |
| 格式 | zip | ||
| 文件大小 | 912.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-12 09:06:39 | ||
图片预览



文档简介
课件14张PPT。黔江区舟白中学--粟永镇
E-Mail:416352289@qq.com13.2.6
直角三角形全等的判定
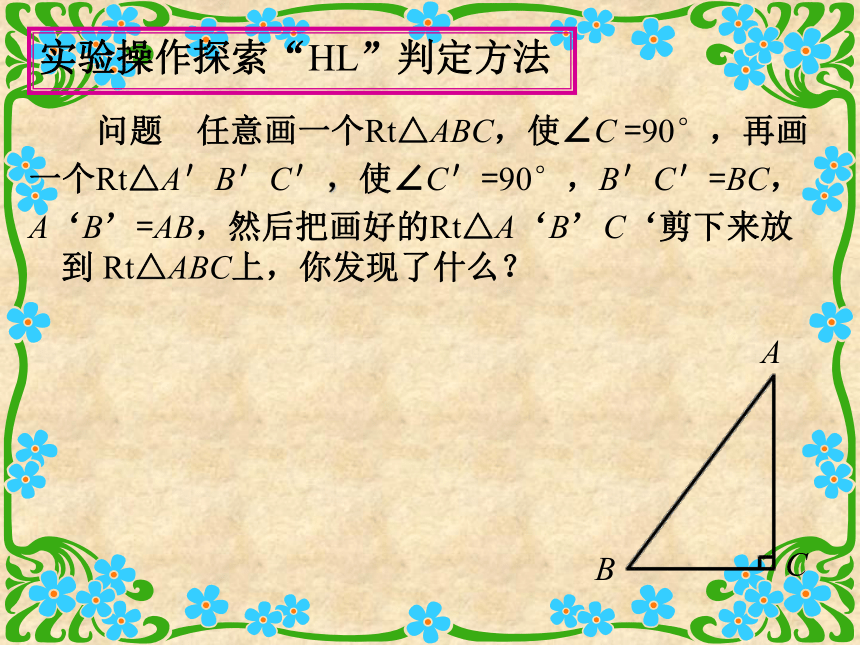
斜边直角边(HL) 问题 任意画一个Rt△ABC,使∠C =90°,再画
一个Rt△A'B'C',使∠C'=90°,B'C'=BC,
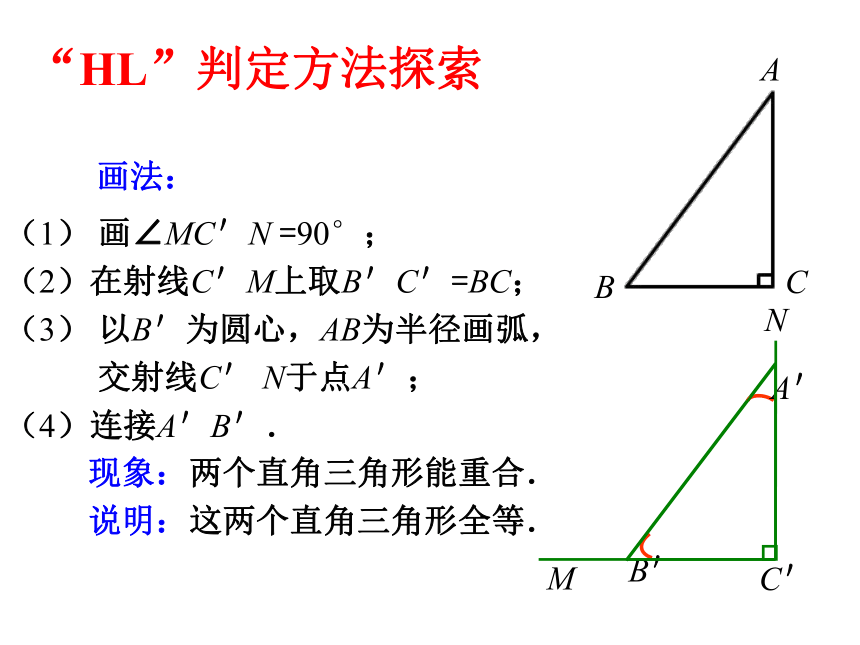
A‘B’=AB,然后把画好的Rt△A‘B’C‘剪下来放到 Rt△ABC上,你发现了什么?实验操作探索“HL”判定方法(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B'为圆心,AB为半径画弧,
交射线C' N于点A';
(4)连接A'B'.“HL”判定方法探索 现象:两个直角三角形能重合.
说明:这两个直角三角形全等. 画法:“HL”判定方法 斜边和一条直角边分别相等的两个直角三角形全
等(简写为“斜边、直角边”或“HL”).数学语言:
∵ 在Rt△ABC 和 Rt△A'B'C'中,
AB =A'B',
BC =B'C',
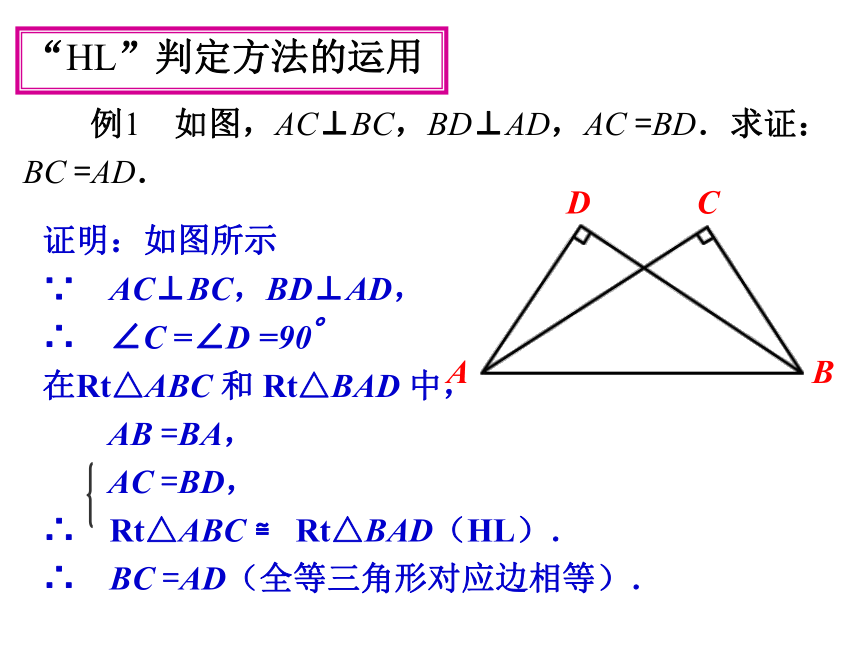
∴ Rt△ABC ≌ Rt△A'B'C'(HL) .证明:如图所示
∵ AC⊥BC,BD⊥AD,
∴ ∠C =∠D =90。
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).“HL”判定方法的运用 例1 如图,AC⊥BC,BD⊥AD,AC =BD.求证:
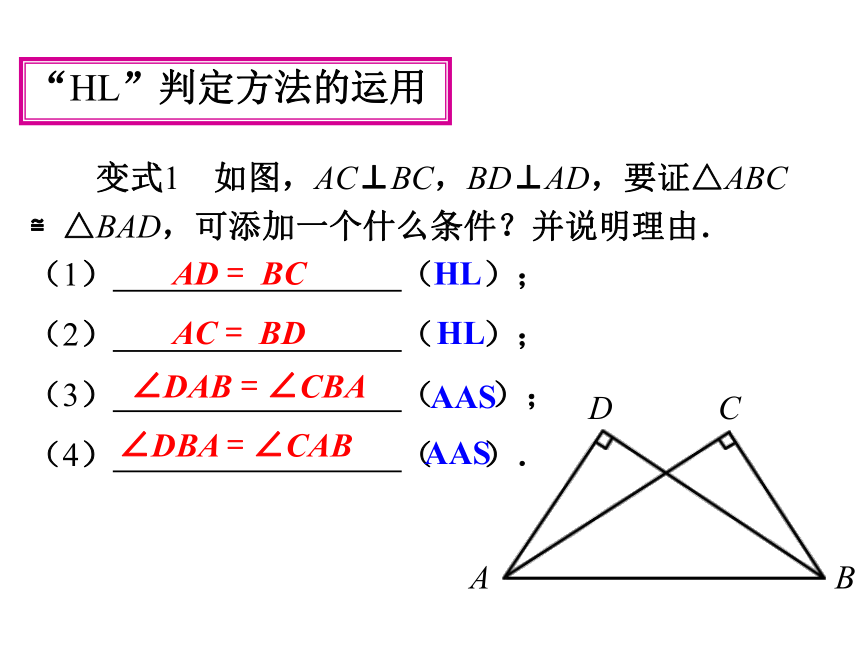
BC =AD. 变式1 如图,AC⊥BC,BD⊥AD,要证△ABC
≌△BAD,可添加一个什么条件?并说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).AD = BCAC = BD∠DAB = ∠CBA∠DBA = ∠CABHLHLAAS AAS“HL”判定方法的运用“HL”判定方法的运用例 如图,有两个长度相同的滑梯(BC=EF),左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?∠ABC +∠DFE =90° ∴ ∠ABC =∠DFE =90° BC =EF,
AC =DF,∴ Rt△ABC ≌ Rt△DEF(HL). ∵ ∠DEF +∠DFE =90°,
∴ ∠ABC +∠DFE =90°. 证明:如图所示∵ AC⊥AB,DE⊥DF,在Rt△ABC 和 Rt△DEF 中,∴ ∠ABC =∠DEF (全等三角形对应角相等).如图,△ABC中,BD和CE分别是边AC和AB上的高,且BD=CE。
求证:∠ABC=∠ACB证明:如图所示∵ BD和CE分别是边AC和AB上的高∴∠BEC=∠CDB= 90°在Rt△BEC 和 Rt△CDB 中,∵ BC=CB
BD=CE∴ Rt△BEC ≌ Rt△CDB(HL)∴ ∠EBC=∠DCB即 ∠ABC=∠ACB 如图,四边形ABCD中,AB=AD,∠B=∠D= 90°。求证:BC=DC提示,可连接AC,
用“HL”证明三角形全等可得课堂练习 练习1 如图,C 是路段AB 的中点,两人从C 同时
出发,以相同的速度分别沿
两条直线行走,并同时到达
D,E 两地.DA⊥AB,EB⊥
AB. D,E 与路段AB的距离
相等吗?为什么?课堂练习 练习2 如图,AB =CD,AE⊥BC,DF⊥BC,垂
足分别为E ,F,CE =BF.求证:AE =DF.(1)“HL”判定方法应满足什么条件?与之前所学
的四种判定方法有什么不同?
(2)判定两个直角三角形全等有哪些方法?课堂小结 作业
同步练习册
直角三角形全等的判定
斜边直角边(HL) 问题 任意画一个Rt△ABC,使∠C =90°,再画
一个Rt△A'B'C',使∠C'=90°,B'C'=BC,
A‘B’=AB,然后把画好的Rt△A‘B’C‘剪下来放到 Rt△ABC上,你发现了什么?实验操作探索“HL”判定方法(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B'为圆心,AB为半径画弧,
交射线C' N于点A';
(4)连接A'B'.“HL”判定方法探索 现象:两个直角三角形能重合.
说明:这两个直角三角形全等. 画法:“HL”判定方法 斜边和一条直角边分别相等的两个直角三角形全
等(简写为“斜边、直角边”或“HL”).数学语言:
∵ 在Rt△ABC 和 Rt△A'B'C'中,
AB =A'B',
BC =B'C',
∴ Rt△ABC ≌ Rt△A'B'C'(HL) .证明:如图所示
∵ AC⊥BC,BD⊥AD,
∴ ∠C =∠D =90。
在Rt△ABC 和 Rt△BAD 中,
AB =BA,
AC =BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).“HL”判定方法的运用 例1 如图,AC⊥BC,BD⊥AD,AC =BD.求证:
BC =AD. 变式1 如图,AC⊥BC,BD⊥AD,要证△ABC
≌△BAD,可添加一个什么条件?并说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).AD = BCAC = BD∠DAB = ∠CBA∠DBA = ∠CABHLHLAAS AAS“HL”判定方法的运用“HL”判定方法的运用例 如图,有两个长度相同的滑梯(BC=EF),左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯 的倾斜角∠ABC 和∠DFE 的大小有什么关系?为什么?∠ABC +∠DFE =90° ∴ ∠ABC =∠DFE =90° BC =EF,
AC =DF,∴ Rt△ABC ≌ Rt△DEF(HL). ∵ ∠DEF +∠DFE =90°,
∴ ∠ABC +∠DFE =90°. 证明:如图所示∵ AC⊥AB,DE⊥DF,在Rt△ABC 和 Rt△DEF 中,∴ ∠ABC =∠DEF (全等三角形对应角相等).如图,△ABC中,BD和CE分别是边AC和AB上的高,且BD=CE。
求证:∠ABC=∠ACB证明:如图所示∵ BD和CE分别是边AC和AB上的高∴∠BEC=∠CDB= 90°在Rt△BEC 和 Rt△CDB 中,∵ BC=CB
BD=CE∴ Rt△BEC ≌ Rt△CDB(HL)∴ ∠EBC=∠DCB即 ∠ABC=∠ACB 如图,四边形ABCD中,AB=AD,∠B=∠D= 90°。求证:BC=DC提示,可连接AC,
用“HL”证明三角形全等可得课堂练习 练习1 如图,C 是路段AB 的中点,两人从C 同时
出发,以相同的速度分别沿
两条直线行走,并同时到达
D,E 两地.DA⊥AB,EB⊥
AB. D,E 与路段AB的距离
相等吗?为什么?课堂练习 练习2 如图,AB =CD,AE⊥BC,DF⊥BC,垂
足分别为E ,F,CE =BF.求证:AE =DF.(1)“HL”判定方法应满足什么条件?与之前所学
的四种判定方法有什么不同?
(2)判定两个直角三角形全等有哪些方法?课堂小结 作业
同步练习册
