人教版七年级数学上册3.1.2等式的性质 教学课件(共18张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.1.2等式的性质 教学课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 16:50:28 | ||
图片预览



文档简介
(共18张PPT)
等式的性质
学习目标
(1)理解并掌握等式的两个基本性质.
(2)能运用等式的性质解简单的一元一次方程.
(3)通过观察、分析、归纳、总结等式的的性质,体会数学研究的思路和方法,培养学生逻辑推理能力.
(4)通过天平的例子来类比等式的性质,提高学生解决问题能力和创新能力.
重点
等式的
性
质
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
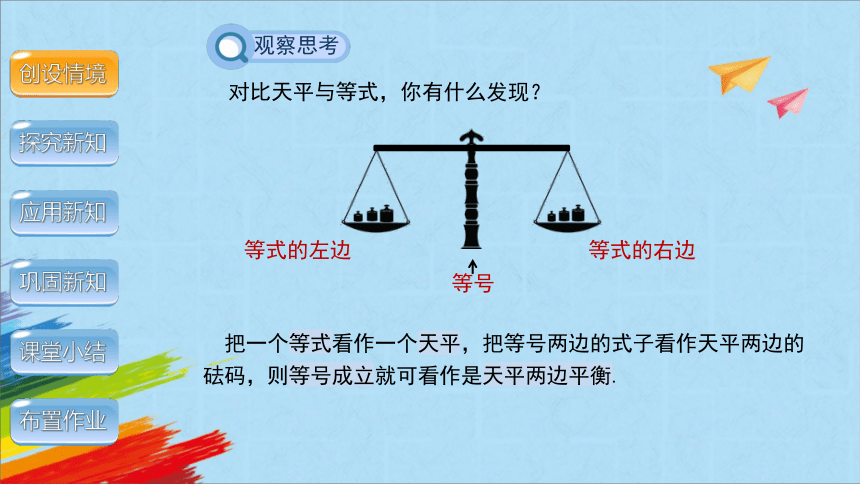
对比天平与等式,你有什么发现?
观察思考
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平两边平衡.
等号
等式的左边
等式的右边
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
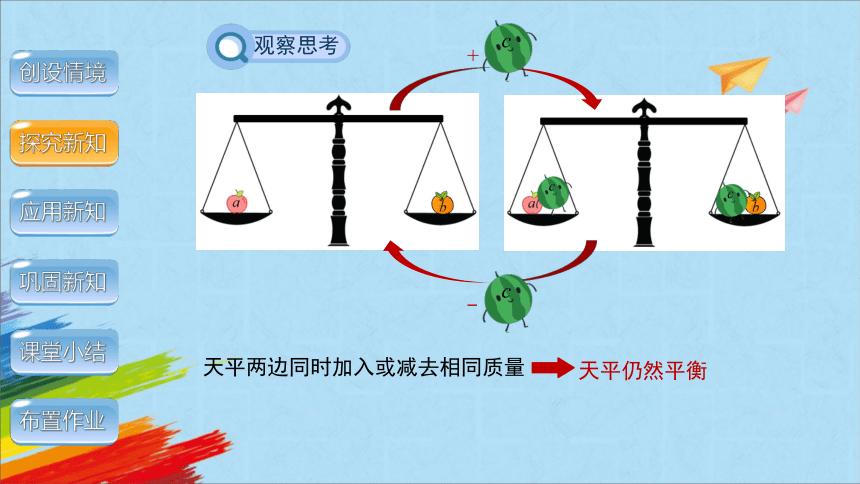
观察思考
+
c
-
c
天平两边同时加入或减去相同质量
天平仍然平衡
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
+
c
-
c
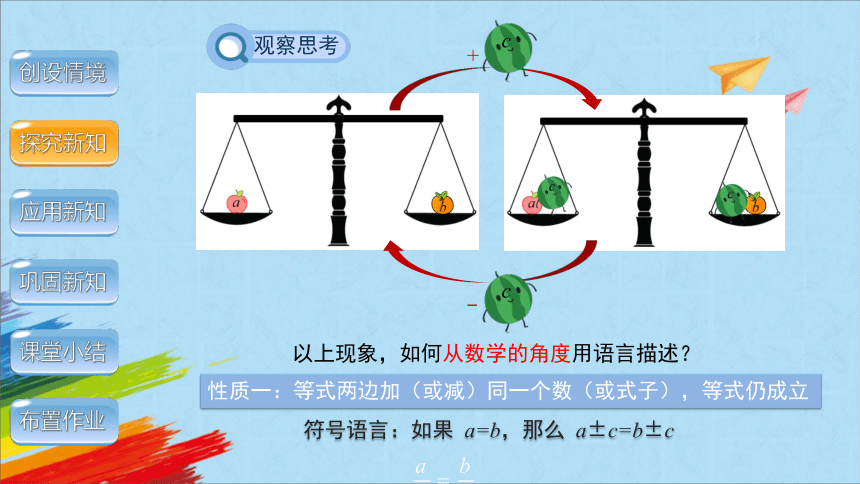
以上现象,如何从数学的角度用语言描述?
性质一:等式两边加(或减)同一个数(或式子),等式仍成立
符号语言:如果 a=b,那么 a±c=b±c
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
6
思考
在下面的括号内填上适当的数或者式子:
(1)因为 2x-6=4,
所以 2x-6+6=4+( ) .
(2)因为 10x-9=8-6x,
所以 10x-9+( ) =8-6x+6x .
(3)因为 3x=2x-8,
所以 3x+( ) =2x-8-2x .
6x
-2x
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
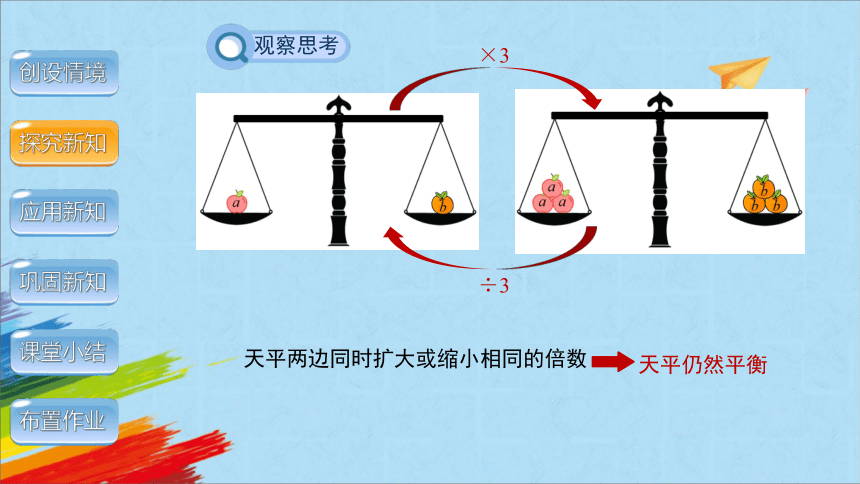
观察思考
×3
天平两边同时扩大或缩小相同的倍数
天平仍然平衡
÷3
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
×3
÷3
以上现象,如何从数学的角度用语言描述?
性质二:等式两边乘同一个数,或除以同一个不为0的数,等式仍成立
符号语言:如果 a=b,那么 ac=bc(c可以是任意数)
如果 a=b(c≠0),那么
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
(2) 如果3+x = 1 成立,x = -2成立吗 依据是什么?
(3) 如果4x=12成立, x =3成立吗 依据是什么?
成立,依据【等式的性质1】 两边同时减3.
成立,依据【等式的性质2】 两边同时除以4或同乘 .
成立,依据【等式的性质2】 两边同乘100或除以 .
(1) 如果 x-5 = y-5 成立, x = y成立吗 依据是什么?
成立,依据【等式的性质1】 两边同时加5.
(4) 如果 成立,a = b成立吗 依据是什么?
利用等式性质解决下列问题
等式的性质1:
激动人心的时刻马上要开
始了,纸笔都准备好喽~
等式两边加(或减)同一个数(或式子),等式仍成立.
归纳总结
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
即:如果a=b,那么a±c=b±c.
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,等式仍成立.
即:如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
利用等式的性质解下列方程:
解方程
把方程转化为 x=a(常数)的形式.
方程两边减7,得
等式的性质1
解:
x+7-7=26-7
x=19
等式的性质
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
利用等式的性质解下列方程:
方程两边除以-5,得
等式的性质2
解:
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
利用等式的性质解下列方程:
方程两边加5,得
解:
方程两边乘-3 ,得
等式的性质1
等式的性质2
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
利用等式的性质判断:
( )
( )
( )
( )
( )
( )
(1)如果 x=y ,那么 x+3=y+3
(2)如果 x=y ,那么 2x-a=2y-a
(3)如果 5x=-10 ,那么 x=2
(4)如果 x+2=5 ,那么 x=7
(5)如果 ax=ay ,那么 x=y
(6)如果 x=y ,那么 ax=ay
×
√
√
×
×
√
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
(1) x+6 = 17 ;
(2) -3x = 15 ;
(4)
(3) 2x-1 = -3 ;
(1)方程两边减6,得
x=11.
(2)方程两边除以-3,得
x=-5.
(3)方程两边加1,得
2x =-2.
方程两边除以2,得
x =-1.
方程两边乘-3,得
x =9.
利用等式的性质解下列方程:
(4)方程两边减1,得
解:
性质1
性质2
应用
如果a=b,那么a±c=b±c.
运用等式的性质解一元一次方程,
即把方程转化为 x=a(常数) 的形式.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
等式的性质
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
布置作业
教科书第83页习题3.1
第1,2,3,4题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
等式的性质
学习目标
(1)理解并掌握等式的两个基本性质.
(2)能运用等式的性质解简单的一元一次方程.
(3)通过观察、分析、归纳、总结等式的的性质,体会数学研究的思路和方法,培养学生逻辑推理能力.
(4)通过天平的例子来类比等式的性质,提高学生解决问题能力和创新能力.
重点
等式的
性
质
难点
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
对比天平与等式,你有什么发现?
观察思考
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平两边平衡.
等号
等式的左边
等式的右边
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
+
c
-
c
天平两边同时加入或减去相同质量
天平仍然平衡
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
+
c
-
c
以上现象,如何从数学的角度用语言描述?
性质一:等式两边加(或减)同一个数(或式子),等式仍成立
符号语言:如果 a=b,那么 a±c=b±c
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
6
思考
在下面的括号内填上适当的数或者式子:
(1)因为 2x-6=4,
所以 2x-6+6=4+( ) .
(2)因为 10x-9=8-6x,
所以 10x-9+( ) =8-6x+6x .
(3)因为 3x=2x-8,
所以 3x+( ) =2x-8-2x .
6x
-2x
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
×3
天平两边同时扩大或缩小相同的倍数
天平仍然平衡
÷3
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
观察思考
×3
÷3
以上现象,如何从数学的角度用语言描述?
性质二:等式两边乘同一个数,或除以同一个不为0的数,等式仍成立
符号语言:如果 a=b,那么 ac=bc(c可以是任意数)
如果 a=b(c≠0),那么
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
思考
(2) 如果3+x = 1 成立,x = -2成立吗 依据是什么?
(3) 如果4x=12成立, x =3成立吗 依据是什么?
成立,依据【等式的性质1】 两边同时减3.
成立,依据【等式的性质2】 两边同时除以4或同乘 .
成立,依据【等式的性质2】 两边同乘100或除以 .
(1) 如果 x-5 = y-5 成立, x = y成立吗 依据是什么?
成立,依据【等式的性质1】 两边同时加5.
(4) 如果 成立,a = b成立吗 依据是什么?
利用等式性质解决下列问题
等式的性质1:
激动人心的时刻马上要开
始了,纸笔都准备好喽~
等式两边加(或减)同一个数(或式子),等式仍成立.
归纳总结
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
即:如果a=b,那么a±c=b±c.
等式的性质2:
等式两边乘同一个数,或除以同一个不为0的数,等式仍成立.
即:如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
利用等式的性质解下列方程:
解方程
把方程转化为 x=a(常数)的形式.
方程两边减7,得
等式的性质1
解:
x+7-7=26-7
x=19
等式的性质
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
利用等式的性质解下列方程:
方程两边除以-5,得
等式的性质2
解:
探究新知
巩固新知
课堂小结
布置作业
应用新知
典型例题
创设情境
利用等式的性质解下列方程:
方程两边加5,得
解:
方程两边乘-3 ,得
等式的性质1
等式的性质2
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
利用等式的性质判断:
( )
( )
( )
( )
( )
( )
(1)如果 x=y ,那么 x+3=y+3
(2)如果 x=y ,那么 2x-a=2y-a
(3)如果 5x=-10 ,那么 x=2
(4)如果 x+2=5 ,那么 x=7
(5)如果 ax=ay ,那么 x=y
(6)如果 x=y ,那么 ax=ay
×
√
√
×
×
√
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
(1) x+6 = 17 ;
(2) -3x = 15 ;
(4)
(3) 2x-1 = -3 ;
(1)方程两边减6,得
x=11.
(2)方程两边除以-3,得
x=-5.
(3)方程两边加1,得
2x =-2.
方程两边除以2,得
x =-1.
方程两边乘-3,得
x =9.
利用等式的性质解下列方程:
(4)方程两边减1,得
解:
性质1
性质2
应用
如果a=b,那么a±c=b±c.
运用等式的性质解一元一次方程,
即把方程转化为 x=a(常数) 的形式.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
等式的性质
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
布置作业
教科书第83页习题3.1
第1,2,3,4题
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
