人教版七年级数学上册3.4实际问题与一元一次方程3:销售中的盈亏 教学课件(共17张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.4实际问题与一元一次方程3:销售中的盈亏 教学课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 17:06:36 | ||
图片预览






文档简介
(共17张PPT)
3.4 实际问题与一元一次方程3
销售中的盈亏
学习目标
1.经历“把销售中的盈亏问题抽象为数学方程”的过程,掌握用一元一次方程解决实际问题的方法与步骤,获得分析实际问题的思路与方法;
2.能够“找出销售中的盈亏问题中的已知数和未知数,分析它们之间的关系,设未知数,列出方程表示问题中的等量关系”;
3.经历“把销售中的盈亏问题抽象为数学方程”的过程,培养学生的数学抽象和数学建模的核心素养,并养成良好的运算习惯;
4.通过探究如何用一元一次方程解决实际问题,体会利用一元一次方程解决问题的基本过程,感受数学的应用价值,提高分析问题、解决问题的能力.
实际问题与一元一次方程
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
1.商品进价是150元,售价是180元,则利润是______元,利润率是________.
2.某种商品进价1000元,标价1500元,若按标价7折销售,售价为______元,利润是_______元,利润率是______.
3.某商品原来每件零售价是a元,现在每件降价10%,降价后每件零售价是________元.
4.一件衣服进价50元,如果卖出后盈利20%,那么商品的利润是______元;如果卖出后亏损20%,那么商品的利润是_____元.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
20%
30
0.9a
1050
50
5%
10
-10
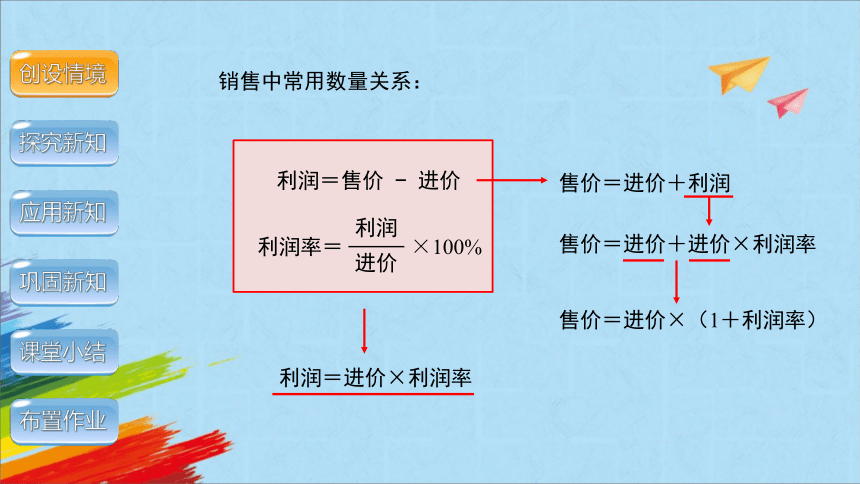
销售中常用数量关系:
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
售价=进价×(1+利润率)
利润=售价 进价
利润=进价×利润率
售价=进价+利润
售价=进价+进价×利润率
利润率=
×100%
利润
进价
例1:一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
分析:两件衣服共卖了120(=60×2)元,是盈是亏要看这家商店买进这两件衣服时花了多少钱.
等量关系:售价=进价+利润
巩固新知
课堂小结
布置作业
典型例题
先大体估算盈亏,再通过准确计算检验!
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
典型例题
探究新知
应用新知
由此得
解:设盈利25%的那件衣服进价x元.
检验, 符合题意.
创设情境
例1:一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
设亏损25%的那件衣服进价y元.
由此得
检验, 符合题意.
先大体估算盈亏,再通过准确计算检验!
等量关系:售价=进价+利润
两件衣服进价 元,而两件衣服的售价是60+60=120元.
答:卖这两件衣服共亏8元.
巩固新知
课堂小结
布置作业
典型例题
探究新知
应用新知
列、解方程后得出的结论与你先前的估算一致吗?
创设情境
例1:一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
通过探究,你对方程在实际问题中的应用有什么新认识?
先大体估算盈亏,再通过准确计算检验!
2.方程是刻画现实世界的一种有效的方法(数学模型);
3....
1.正确运用数学知识分析问题可以减少直觉判断的错误;
例2:某商店四月份购进70个篮球,由于供不应求,五月份又购进同种篮球60个,两次购进篮球的单价不同,已知四月份和五月份购进篮球的单价和为65元,并且四月份与五月份购入篮球总费用相同.
(1)求该商店四、五月份购进篮球的单价分别是多少元;
典型例题
等量关系: 四月总费用 = 五月总费用
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
四月:
五月:
70个
60个
单价和为65元
. . .
. . .
单价分别是多少元?
?
?
典型例题
等量关系: 四月总费用 = 五月总费用
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
四月:
五月:
70个
60个
单价和为65元
. . .
. . .
单价分别是多少元?
?
?
由此得
检验, 符合题意.
解:设四月份购买篮球的单价为x元,则五月份购买的篮球单价为 元.
答:四月购买篮球的单价是30元,五月份购买的篮球单价是 元.
典型例题
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
70个
60个
单价:30元
(2)由于运输不当,五月份购进的篮球中有10%损坏,不能卖售,该商店将两批篮球按同一价格全部销售后,获利不低于2000元,求每个篮球的售价至少是多少元(售价请取整).
单价:35元
等量关系:利润=售价 进价
由此得
检验, 符合题意.
答:每个篮球的售价为49元,获利不低于2000元.
解:设每个篮球的售价为x元.
等量关系:售价 进价=利润
四月:
五月:
. . .
. . .
1.某股民将甲、乙两种股票卖出,甲种股票卖出1500元,盈利20%,乙种股票卖出1600元,但亏损20%,该股民在这次交易中是盈利还是亏损,盈利或亏损多少元?
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
由此得
解:设甲种股票原价x元.
检验, 符合题意.
设乙种股票原价y元.
由此得
检验, 符合题意.
等量关系:售价=进价×(1+利润率)
答:股民亏损150元.
甲乙股票原价 元,卖出1500+1600=3100元.
2.据气象局预测2022年将迎来一个寒冬,某商店根据此商机购进一批优质手套,按进价提高40%后标价,为了增加销量,该商店决定打八折出售,即每副手套以28元售出.
(1)求这批手套的进价是每副多少元.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解方程,得
答:这批手套的进价是每副25元.
解:设这批手套的进价是每副x元.
检验, 符合题意.
等量关系:售价=进价×(1+利润率)×折扣
(2)该商店当售出这批手套一半数量后,正好赶上双十一活动,所以决定改变促销方式,该商店决定将剩下的手套以每3副80元的价格销售,很快全部售完,这批手套该商店共获利2800元,求该商店共购进多少副手套.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解方程,得
答:该商店共购进1200副手套.
解:设该商店共购进y副手套.
检验, 符合题意.
等量关系:利润1 +利润2 =总利润
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
列一元一次方程解决实际问题的基本过程:
实际
问题
实际问题与
一元一次方程
(销售中的盈亏)
一元一次
方程
一元一次
方程的解
实际问题的答案
等量关系:
利润=售价 进价
设未知数,列方程
解方程
检验解符合题意
抽象出数学模型
回到实际问题
利润率=
×100%
利润
进价
布置作业
教科书
第106页练习第1题;
第106页习题3.4第6、11题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
3.4 实际问题与一元一次方程3
销售中的盈亏
学习目标
1.经历“把销售中的盈亏问题抽象为数学方程”的过程,掌握用一元一次方程解决实际问题的方法与步骤,获得分析实际问题的思路与方法;
2.能够“找出销售中的盈亏问题中的已知数和未知数,分析它们之间的关系,设未知数,列出方程表示问题中的等量关系”;
3.经历“把销售中的盈亏问题抽象为数学方程”的过程,培养学生的数学抽象和数学建模的核心素养,并养成良好的运算习惯;
4.通过探究如何用一元一次方程解决实际问题,体会利用一元一次方程解决问题的基本过程,感受数学的应用价值,提高分析问题、解决问题的能力.
实际问题与一元一次方程
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
1.商品进价是150元,售价是180元,则利润是______元,利润率是________.
2.某种商品进价1000元,标价1500元,若按标价7折销售,售价为______元,利润是_______元,利润率是______.
3.某商品原来每件零售价是a元,现在每件降价10%,降价后每件零售价是________元.
4.一件衣服进价50元,如果卖出后盈利20%,那么商品的利润是______元;如果卖出后亏损20%,那么商品的利润是_____元.
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
20%
30
0.9a
1050
50
5%
10
-10
销售中常用数量关系:
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
售价=进价×(1+利润率)
利润=售价 进价
利润=进价×利润率
售价=进价+利润
售价=进价+进价×利润率
利润率=
×100%
利润
进价
例1:一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
分析:两件衣服共卖了120(=60×2)元,是盈是亏要看这家商店买进这两件衣服时花了多少钱.
等量关系:售价=进价+利润
巩固新知
课堂小结
布置作业
典型例题
先大体估算盈亏,再通过准确计算检验!
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
典型例题
探究新知
应用新知
由此得
解:设盈利25%的那件衣服进价x元.
检验, 符合题意.
创设情境
例1:一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
设亏损25%的那件衣服进价y元.
由此得
检验, 符合题意.
先大体估算盈亏,再通过准确计算检验!
等量关系:售价=进价+利润
两件衣服进价 元,而两件衣服的售价是60+60=120元.
答:卖这两件衣服共亏8元.
巩固新知
课堂小结
布置作业
典型例题
探究新知
应用新知
列、解方程后得出的结论与你先前的估算一致吗?
创设情境
例1:一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
通过探究,你对方程在实际问题中的应用有什么新认识?
先大体估算盈亏,再通过准确计算检验!
2.方程是刻画现实世界的一种有效的方法(数学模型);
3....
1.正确运用数学知识分析问题可以减少直觉判断的错误;
例2:某商店四月份购进70个篮球,由于供不应求,五月份又购进同种篮球60个,两次购进篮球的单价不同,已知四月份和五月份购进篮球的单价和为65元,并且四月份与五月份购入篮球总费用相同.
(1)求该商店四、五月份购进篮球的单价分别是多少元;
典型例题
等量关系: 四月总费用 = 五月总费用
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
四月:
五月:
70个
60个
单价和为65元
. . .
. . .
单价分别是多少元?
?
?
典型例题
等量关系: 四月总费用 = 五月总费用
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
四月:
五月:
70个
60个
单价和为65元
. . .
. . .
单价分别是多少元?
?
?
由此得
检验, 符合题意.
解:设四月份购买篮球的单价为x元,则五月份购买的篮球单价为 元.
答:四月购买篮球的单价是30元,五月份购买的篮球单价是 元.
典型例题
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
70个
60个
单价:30元
(2)由于运输不当,五月份购进的篮球中有10%损坏,不能卖售,该商店将两批篮球按同一价格全部销售后,获利不低于2000元,求每个篮球的售价至少是多少元(售价请取整).
单价:35元
等量关系:利润=售价 进价
由此得
检验, 符合题意.
答:每个篮球的售价为49元,获利不低于2000元.
解:设每个篮球的售价为x元.
等量关系:售价 进价=利润
四月:
五月:
. . .
. . .
1.某股民将甲、乙两种股票卖出,甲种股票卖出1500元,盈利20%,乙种股票卖出1600元,但亏损20%,该股民在这次交易中是盈利还是亏损,盈利或亏损多少元?
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
由此得
解:设甲种股票原价x元.
检验, 符合题意.
设乙种股票原价y元.
由此得
检验, 符合题意.
等量关系:售价=进价×(1+利润率)
答:股民亏损150元.
甲乙股票原价 元,卖出1500+1600=3100元.
2.据气象局预测2022年将迎来一个寒冬,某商店根据此商机购进一批优质手套,按进价提高40%后标价,为了增加销量,该商店决定打八折出售,即每副手套以28元售出.
(1)求这批手套的进价是每副多少元.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解方程,得
答:这批手套的进价是每副25元.
解:设这批手套的进价是每副x元.
检验, 符合题意.
等量关系:售价=进价×(1+利润率)×折扣
(2)该商店当售出这批手套一半数量后,正好赶上双十一活动,所以决定改变促销方式,该商店决定将剩下的手套以每3副80元的价格销售,很快全部售完,这批手套该商店共获利2800元,求该商店共购进多少副手套.
探究新知
应用新知
课堂小结
布置作业
巩固新知
随堂练习
创设情境
解方程,得
答:该商店共购进1200副手套.
解:设该商店共购进y副手套.
检验, 符合题意.
等量关系:利润1 +利润2 =总利润
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
列一元一次方程解决实际问题的基本过程:
实际
问题
实际问题与
一元一次方程
(销售中的盈亏)
一元一次
方程
一元一次
方程的解
实际问题的答案
等量关系:
利润=售价 进价
设未知数,列方程
解方程
检验解符合题意
抽象出数学模型
回到实际问题
利润率=
×100%
利润
进价
布置作业
教科书
第106页练习第1题;
第106页习题3.4第6、11题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
