人教版七年级数学上册3.4实际问题与一元一次方程5:电话计费问题 教学课件(共30张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.4实际问题与一元一次方程5:电话计费问题 教学课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 17:07:23 | ||
图片预览




文档简介
(共30张PPT)
3.4 实际问题与一元一次方程5
配套人教版
电话计费问题
学习目标
1.经历“把不同计费问题抽象为数学方程”的过程,理解方程不仅能计算未知数的值,而且可以进一步解方案设计类应用题;
2.通过探究不同计费问题,能从多种信息表达形式中获取有关信息,经历先分类再综合的思考,能运用方程找到问题的关键所在;
3.经历“把不同计费问题抽象为数学方程”的过程,体会模型化的思维,培养学生数学建模的核心素养;
4.通过探究实际问题,体会利用一元一次方程解决实际问题,感受数学的应用价值,提高分析问题、解决问题的能力.
电话计费问题
观察思考
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
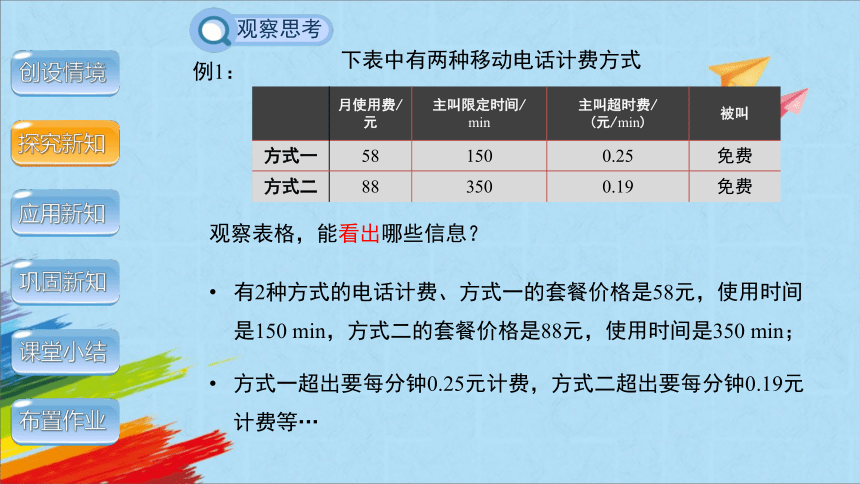
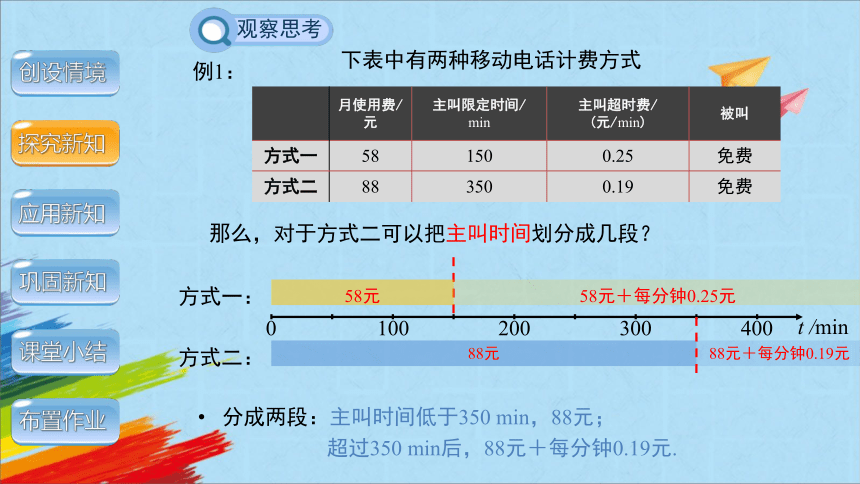
下表中有两种移动电话计费方式
观察表格,能看出哪些信息?
有2种方式的电话计费、方式一的套餐价格是58元,使用时间是150 min,方式二的套餐价格是88元,使用时间是350 min;
方式一超出要每分钟0.25元计费,方式二超出要每分钟0.19元计费等…
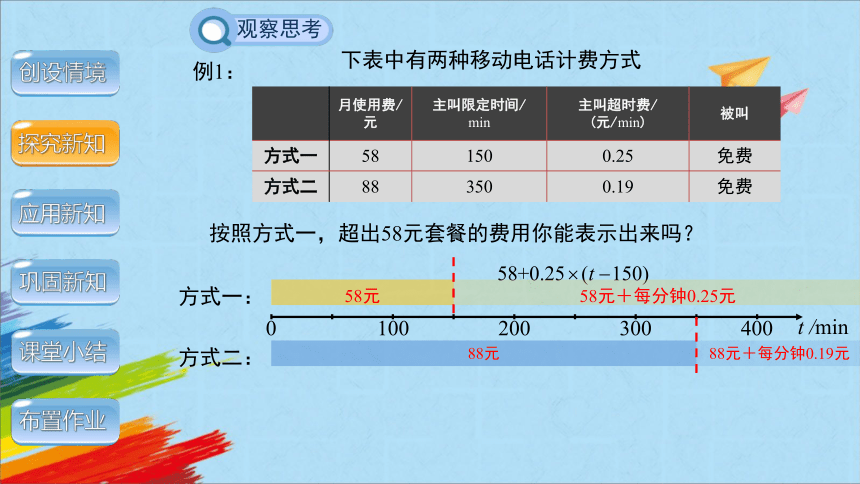
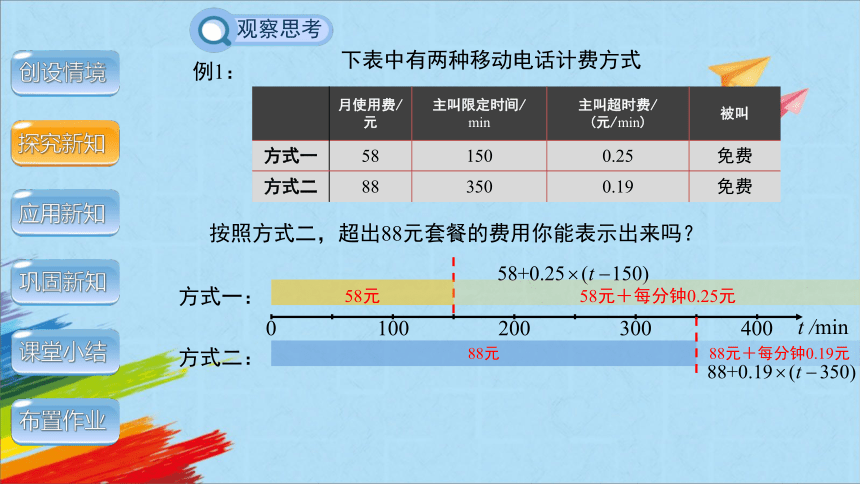
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
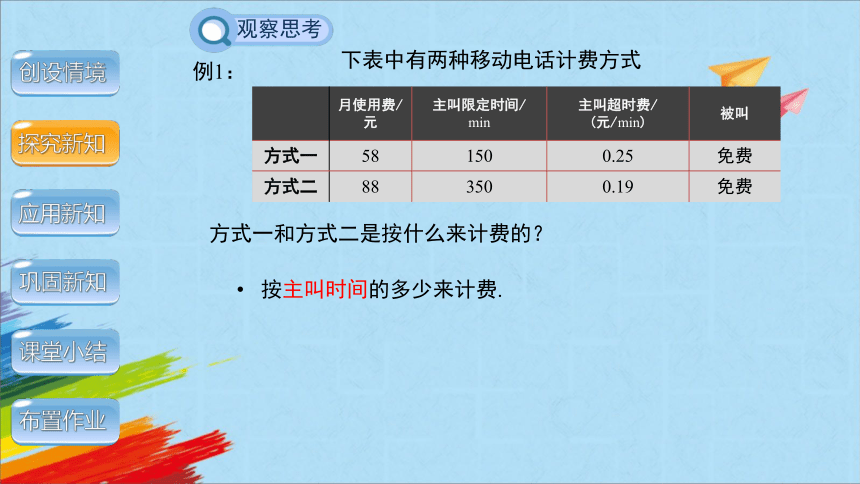
按主叫时间的多少来计费.
观察思考
方式一和方式二是按什么来计费的?
下表中有两种移动电话计费方式
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
58元+每分钟0.25元
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
t /min
0
100
200
300
400
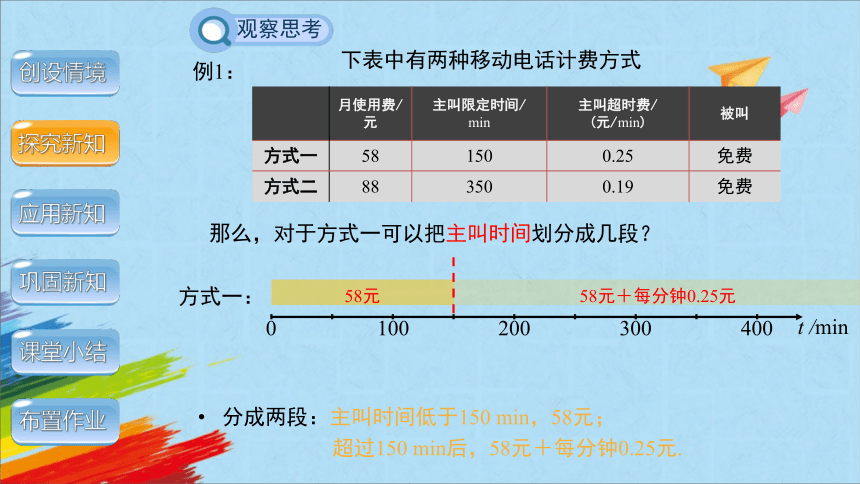
方式一:
58元
下表中有两种移动电话计费方式
那么,对于方式一可以把主叫时间划分成几段?
分成两段:主叫时间低于150 min,58元;
超过150 min后,58元+每分钟0.25元.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
t /min
0
100
200
300
400
方式一:
方式二:
88元
88元+每分钟0.19元
下表中有两种移动电话计费方式
那么,对于方式二可以把主叫时间划分成几段?
分成两段:主叫时间低于350 min,88元;
超过350 min后,88元+每分钟0.19元.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
58元+每分钟0.25元
58元
按照方式一,超出58元套餐的费用你能表示出来吗?
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
t /min
0
100
200
300
400
方式一:
方式二:
下表中有两种移动电话计费方式
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
88元
88元+每分钟0.19元
58元+每分钟0.25元
58元
按照方式二,超出88元套餐的费用你能表示出来吗?
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
t /min
0
100
200
300
400
方式一:
方式二:
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
下表中有两种移动电话计费方式
例1:
88元
88元+每分钟0.19元
58元+每分钟0.25元
58元
巩固新知
课堂小结
布置作业
创设情境
观察思考
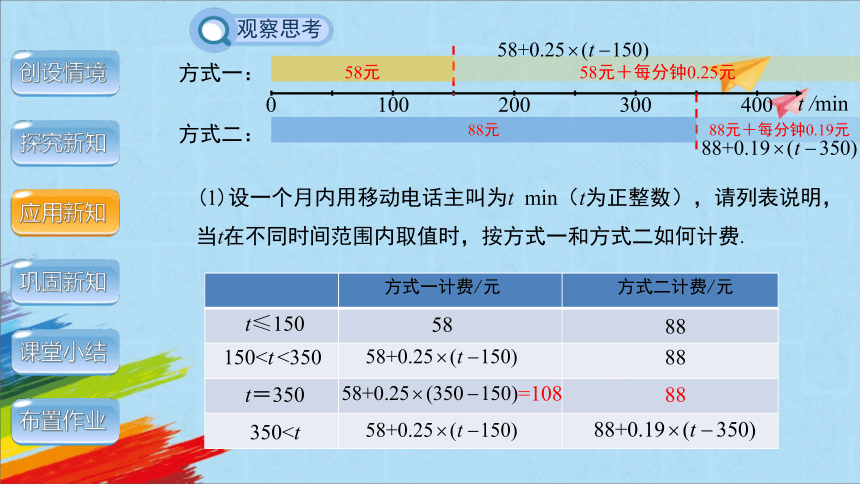
(1)设一个月内用移动电话主叫为t min(t为正整数),请列表说明,当t在不同时间范围内取值时,按方式一和方式二如何计费.
方式一计费/元
t≤150
150<350
58
350方式二计费/元
88
88
t=350
88
=108
探究新知
应用新知
t /min
0
100
200
300
400
方式一:
方式二:
88元
88元+每分钟0.19元
58元+每分钟0.25元
58元
②当150≤t≤350时,方式一花费从58元到108元,方式二花费88元;
即存在某时间点,方式一和方式二计费相同;
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
方式一计费/元
方式二计费/元
等量关系:方式一计费=方式二计费
方式一计费/元
t≤150
58
方式二计费/元
88
88
t=350
88
解:观察上表,分类分析,可以发现:
①当t≤150时,方式一:58元,方式二:88元,照方式一计费划算;
150<350
350在t=270 min时,两种方式计费相等,都是88元;
=108
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
方式一计费/元
t≤150
58
方式二计费/元
88
88
t=350
88
=108
解:观察上表,分类分析,可以发现:
③当t≥350时,方式一花费108+0.25(t 350)元,方式二花费88+0.19(t 350)元,照方式二计费划算.
综合以上分类思考,可以发现:
当t<270时,选择方案一省钱;
当t>270时,选择方案二省钱;
150<350
350在t=270 min时,两种方式计费相等,都是88元;
②当150≤t≤350时,方式一花费从58元到108元,方式二花费88元;
①当t≤150时,方式一:58元,方式二:88元,照方式一计费划算;
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
方案一:工厂污水先净化处理后再排出,每处理1 m3污水所用的原料费为2元,并且每月排污设备损耗为30000元.
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
典型例题
问:如果你作为厂长在不污染环境又节约资金的前提下应选用哪种处理污水的方案?请通过计算加以说明?
方案二:工厂将污水排到污水厂统一处理,每处理1 m3污水需付14元的排污费.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
能看出哪些信息?
有2种处理污水的方式、方式一工厂污水先净化处理后再排出、方式二是工厂将污水排到污水厂统一处理、不同方式污水处理的方式需要不同的费用等…
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
方案一:工厂污水先净化处理后再排出,每处理1 m3污水所用的原料费为2元,并且每月排污设备损耗为30000元.
方案二:工厂将污水排到污水厂统一处理,每处理1 m3污水需付14元的排污费.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
方式一和方式二是按什么来计费?
按污水的排放量的多少来计费.
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
方案一:工厂污水先净化处理后再排出,每处理1m3污水所用的原料费为2元,并且每月排污设备损耗为30000元.
方案二:工厂将污水排到污水厂统一处理,每处理1m3污水需付14元的排污费.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
可以把方式一和方式二的费用表示出来吗?
解:设工厂每月生产x件产品,则污水费用为:
方式一:
方式二:
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
方案一:工厂污水先净化处理后再排出,每处理1m3污水所用的原料费为2元,并且每月排污设备损耗为30000元.
方案二:工厂将污水排到污水厂统一处理,每处理1m3污水需付14元的排污费.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
解:设工厂每月生产x件产品,则污水费用为:
方式一:
方式二:
由此可知,当生产某种产品较少时,方式二合适,当生产产品较多时,方式一可能优于方式二.
等量关系:方式一费用=方式二费用
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
由此可知,当生产产品为5000件时,两种方式处理污水费用相同.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
解:设工厂每月生产x件产品,则污水费用为:
方式一:
方式二:
等量关系:方式一费用=方式二费用
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
综合以上分类思考,可以发现:
当x<5000时,选择方案二省钱;
当x>5000时,选择方案一省钱.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
2.利用方程找到关键点;
总结归纳
3.先分类讨论,再综合对比;
4....
1.从多种信息表达形式中获取有关信息;
1.下表中有两种移动电话计费方式:月使用费固定收:主叫不超过限定时间不再收费,主叫超时部分加收超时费;被叫免费.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
(1)若某同学某月主叫通话时间为200分钟,则他按方式一计费需________元,按方式二计费需_______元;若他按方式二计费需107元,则主叫通话时间为______分钟.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 65 160 0.20 免费
方式二 100 380 0.25 免费
73
100
408
65+(200-160)×0.2
=73(元)
380+(107-100)÷0.25
=408(分钟)
1.下表中有两种移动电话计费方式:月使用费固定收:主叫不超过限定时间不再收费,主叫超时部分加收超时费;被叫免费.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等?若存在,请求出t的值;若不存在,请说明理由.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 65 160 0.20 免费
方式二 100 380 0.25 免费
解:设某同学某月主叫通话时间为t分钟.
解方程,得
等量关系:方式一计费=方式二计费
情况一
由此可知,当主叫时间为335分钟时,两种方式计费相同,都是100元.
1.下表中有两种移动电话计费方式:月使用费固定收:主叫不超过限定时间不再收费,主叫超时部分加收超时费;被叫免费.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 65 160 0.20 免费
方式二 100 380 0.25 免费
解方程,得
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等?若存在,请求出t的值;若不存在,请说明理由.
解:设某同学某月主叫通话时间为t分钟.
等量关系:方式一计费=方式二计费
由此可知,当主叫时间为560分钟时,两种方式计费再次相同,都是145元.
(元)
情况二
1.下表中有两种移动电话计费方式:月使用费固定收:主叫不超过限定时间不再收费,主叫超时部分加收超时费;被叫免费.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
(3)直接写出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 65 160 0.20 免费
方式二 100 380 0.25 免费
方式一计费/元
t≤160
160<380
65
t>380
方式二计费/元
100
100
t=380
100
=109
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
方式一计费/元
t≤160
160<380
65
t>380
方式二计费/元
100
100
t=380
100
=109
解:观察上表,分类分析,可以发现:
①当t≤160时,方式一:65元,方式二:100元,照方式一计费划算;
②当160≤t≤380时,方式一花费从65元到109元,方式二花费100元;
在t=335 min时,两种方式计费相等,都是100元;
③当t≥380时,方式一花费108+0.25(t 350)元,方式二花费88+0.19(t 350)元,在t=560 min时,两种方式计费相等,都是145元;
综合以上分类思考,可以发现:
当t<335时,选择方案一省钱;
当t>560时,选择方案一省钱;
当335探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
(1) 若用x(元)表示商品价格,请你用含x的式子分别表示两种优惠活动所花的钱数.
2.某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
解:x(元)表示商品价格.
优惠一:0.9x
优惠二:缴纳200元会费成为该超市一员,所有商品价格可获得八折优惠.
优惠一:非会员购物,所有商品价格可获九折优惠;
优惠二:200+0.8x
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
(2)当商品价格是多少元时,两种优惠活动所花钱数相同?
2.某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
0.9x=200+0.8x
解得 x=2000
等量关系:优惠一价格=优惠二价格
优惠二:缴纳200元会费成为该超市一员,所有商品价格可获得八折优惠.
优惠一:非会员购物,所有商品价格可获九折优惠;
解:x(元)表示商品价格.
答:当商品价格是2000元时,两种优惠活动所花钱数相同.
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
(3)当某人计划在该超市购买价格为2700元的一台电脑,请分析选哪种优惠更省钱
2.某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
优惠一:2700×0.9=2430元.
优惠二:200+2700×0.8=2360元.
答:选择优惠二更省钱.
优惠二:缴纳200元会费成为该超市一员,所有商品价格可获得八折优惠.
优惠一:非会员购物,所有商品价格可获九折优惠;
综合以上分类思考,可以发现:
当x<2000时,选择优惠一更省钱;
当x>2000时,选择优惠二更省钱.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
3.先分类讨论,再综合对比.
实际问题与
一元一次方程
(电话计费)
1.从多种信息表达形式中获取有关信息;
2.利用方程到关键点;
布置作业
教科书
第106页练习第2题;
第106页习题3.4第12题;
第111页复习题第10题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
3.4 实际问题与一元一次方程5
配套人教版
电话计费问题
学习目标
1.经历“把不同计费问题抽象为数学方程”的过程,理解方程不仅能计算未知数的值,而且可以进一步解方案设计类应用题;
2.通过探究不同计费问题,能从多种信息表达形式中获取有关信息,经历先分类再综合的思考,能运用方程找到问题的关键所在;
3.经历“把不同计费问题抽象为数学方程”的过程,体会模型化的思维,培养学生数学建模的核心素养;
4.通过探究实际问题,体会利用一元一次方程解决实际问题,感受数学的应用价值,提高分析问题、解决问题的能力.
电话计费问题
观察思考
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
下表中有两种移动电话计费方式
观察表格,能看出哪些信息?
有2种方式的电话计费、方式一的套餐价格是58元,使用时间是150 min,方式二的套餐价格是88元,使用时间是350 min;
方式一超出要每分钟0.25元计费,方式二超出要每分钟0.19元计费等…
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
按主叫时间的多少来计费.
观察思考
方式一和方式二是按什么来计费的?
下表中有两种移动电话计费方式
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
58元+每分钟0.25元
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
t /min
0
100
200
300
400
方式一:
58元
下表中有两种移动电话计费方式
那么,对于方式一可以把主叫时间划分成几段?
分成两段:主叫时间低于150 min,58元;
超过150 min后,58元+每分钟0.25元.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
t /min
0
100
200
300
400
方式一:
方式二:
88元
88元+每分钟0.19元
下表中有两种移动电话计费方式
那么,对于方式二可以把主叫时间划分成几段?
分成两段:主叫时间低于350 min,88元;
超过350 min后,88元+每分钟0.19元.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
58元+每分钟0.25元
58元
按照方式一,超出58元套餐的费用你能表示出来吗?
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
t /min
0
100
200
300
400
方式一:
方式二:
下表中有两种移动电话计费方式
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
例1:
88元
88元+每分钟0.19元
58元+每分钟0.25元
58元
按照方式二,超出88元套餐的费用你能表示出来吗?
巩固新知
课堂小结
布置作业
创设情境
探究新知
应用新知
观察思考
t /min
0
100
200
300
400
方式一:
方式二:
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
下表中有两种移动电话计费方式
例1:
88元
88元+每分钟0.19元
58元+每分钟0.25元
58元
巩固新知
课堂小结
布置作业
创设情境
观察思考
(1)设一个月内用移动电话主叫为t min(t为正整数),请列表说明,当t在不同时间范围内取值时,按方式一和方式二如何计费.
方式一计费/元
t≤150
150
58
350
88
88
t=350
88
=108
探究新知
应用新知
t /min
0
100
200
300
400
方式一:
方式二:
88元
88元+每分钟0.19元
58元+每分钟0.25元
58元
②当150≤t≤350时,方式一花费从58元到108元,方式二花费88元;
即存在某时间点,方式一和方式二计费相同;
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
方式一计费/元
方式二计费/元
等量关系:方式一计费=方式二计费
方式一计费/元
t≤150
58
方式二计费/元
88
88
t=350
88
解:观察上表,分类分析,可以发现:
①当t≤150时,方式一:58元,方式二:88元,照方式一计费划算;
150
350
=108
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
方式一计费/元
t≤150
58
方式二计费/元
88
88
t=350
88
=108
解:观察上表,分类分析,可以发现:
③当t≥350时,方式一花费108+0.25(t 350)元,方式二花费88+0.19(t 350)元,照方式二计费划算.
综合以上分类思考,可以发现:
当t<270时,选择方案一省钱;
当t>270时,选择方案二省钱;
150
350
②当150≤t≤350时,方式一花费从58元到108元,方式二花费88元;
①当t≤150时,方式一:58元,方式二:88元,照方式一计费划算;
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
方案一:工厂污水先净化处理后再排出,每处理1 m3污水所用的原料费为2元,并且每月排污设备损耗为30000元.
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
典型例题
问:如果你作为厂长在不污染环境又节约资金的前提下应选用哪种处理污水的方案?请通过计算加以说明?
方案二:工厂将污水排到污水厂统一处理,每处理1 m3污水需付14元的排污费.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
能看出哪些信息?
有2种处理污水的方式、方式一工厂污水先净化处理后再排出、方式二是工厂将污水排到污水厂统一处理、不同方式污水处理的方式需要不同的费用等…
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
方案一:工厂污水先净化处理后再排出,每处理1 m3污水所用的原料费为2元,并且每月排污设备损耗为30000元.
方案二:工厂将污水排到污水厂统一处理,每处理1 m3污水需付14元的排污费.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
方式一和方式二是按什么来计费?
按污水的排放量的多少来计费.
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
方案一:工厂污水先净化处理后再排出,每处理1m3污水所用的原料费为2元,并且每月排污设备损耗为30000元.
方案二:工厂将污水排到污水厂统一处理,每处理1m3污水需付14元的排污费.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
可以把方式一和方式二的费用表示出来吗?
解:设工厂每月生产x件产品,则污水费用为:
方式一:
方式二:
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
方案一:工厂污水先净化处理后再排出,每处理1m3污水所用的原料费为2元,并且每月排污设备损耗为30000元.
方案二:工厂将污水排到污水厂统一处理,每处理1m3污水需付14元的排污费.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
解:设工厂每月生产x件产品,则污水费用为:
方式一:
方式二:
由此可知,当生产某种产品较少时,方式二合适,当生产产品较多时,方式一可能优于方式二.
等量关系:方式一费用=方式二费用
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
由此可知,当生产产品为5000件时,两种方式处理污水费用相同.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
典型例题
解:设工厂每月生产x件产品,则污水费用为:
方式一:
方式二:
等量关系:方式一费用=方式二费用
例2:某工厂生产某种产品,每件产品的出厂价为50元,成本价为25元,因为在生产过程中,平均每生产一件产品有0.5 m3污水排出,为了净化环境,工厂设计了两种处理污水的方案.
综合以上分类思考,可以发现:
当x<5000时,选择方案二省钱;
当x>5000时,选择方案一省钱.
巩固新知
课堂小结
布置作业
探究新知
应用新知
创设情境
2.利用方程找到关键点;
总结归纳
3.先分类讨论,再综合对比;
4....
1.从多种信息表达形式中获取有关信息;
1.下表中有两种移动电话计费方式:月使用费固定收:主叫不超过限定时间不再收费,主叫超时部分加收超时费;被叫免费.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
(1)若某同学某月主叫通话时间为200分钟,则他按方式一计费需________元,按方式二计费需_______元;若他按方式二计费需107元,则主叫通话时间为______分钟.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 65 160 0.20 免费
方式二 100 380 0.25 免费
73
100
408
65+(200-160)×0.2
=73(元)
380+(107-100)÷0.25
=408(分钟)
1.下表中有两种移动电话计费方式:月使用费固定收:主叫不超过限定时间不再收费,主叫超时部分加收超时费;被叫免费.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等?若存在,请求出t的值;若不存在,请说明理由.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 65 160 0.20 免费
方式二 100 380 0.25 免费
解:设某同学某月主叫通话时间为t分钟.
解方程,得
等量关系:方式一计费=方式二计费
情况一
由此可知,当主叫时间为335分钟时,两种方式计费相同,都是100元.
1.下表中有两种移动电话计费方式:月使用费固定收:主叫不超过限定时间不再收费,主叫超时部分加收超时费;被叫免费.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 65 160 0.20 免费
方式二 100 380 0.25 免费
解方程,得
(2)是否存在某主叫通话时间t(分钟),按方式一和方式二的计费相等?若存在,请求出t的值;若不存在,请说明理由.
解:设某同学某月主叫通话时间为t分钟.
等量关系:方式一计费=方式二计费
由此可知,当主叫时间为560分钟时,两种方式计费再次相同,都是145元.
(元)
情况二
1.下表中有两种移动电话计费方式:月使用费固定收:主叫不超过限定时间不再收费,主叫超时部分加收超时费;被叫免费.
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
(3)直接写出当月主叫通话时间t(分钟)满足什么条件时,选择方式一省钱;当每月主叫通话时间t(分钟)满足什么条件时,选择方式二省钱.
月使用费/元 主叫限定时间/ min 主叫超时费/ (元/min) 被叫
方式一 65 160 0.20 免费
方式二 100 380 0.25 免费
方式一计费/元
t≤160
160
65
t>380
方式二计费/元
100
100
t=380
100
=109
随堂练习
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
方式一计费/元
t≤160
160
65
t>380
方式二计费/元
100
100
t=380
100
=109
解:观察上表,分类分析,可以发现:
①当t≤160时,方式一:65元,方式二:100元,照方式一计费划算;
②当160≤t≤380时,方式一花费从65元到109元,方式二花费100元;
在t=335 min时,两种方式计费相等,都是100元;
③当t≥380时,方式一花费108+0.25(t 350)元,方式二花费88+0.19(t 350)元,在t=560 min时,两种方式计费相等,都是145元;
综合以上分类思考,可以发现:
当t<335时,选择方案一省钱;
当t>560时,选择方案一省钱;
当335
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
(1) 若用x(元)表示商品价格,请你用含x的式子分别表示两种优惠活动所花的钱数.
2.某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
解:x(元)表示商品价格.
优惠一:0.9x
优惠二:缴纳200元会费成为该超市一员,所有商品价格可获得八折优惠.
优惠一:非会员购物,所有商品价格可获九折优惠;
优惠二:200+0.8x
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
(2)当商品价格是多少元时,两种优惠活动所花钱数相同?
2.某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
0.9x=200+0.8x
解得 x=2000
等量关系:优惠一价格=优惠二价格
优惠二:缴纳200元会费成为该超市一员,所有商品价格可获得八折优惠.
优惠一:非会员购物,所有商品价格可获九折优惠;
解:x(元)表示商品价格.
答:当商品价格是2000元时,两种优惠活动所花钱数相同.
探究新知
应用新知
课堂小结
布置作业
巩固新知
创设情境
随堂练习
(3)当某人计划在该超市购买价格为2700元的一台电脑,请分析选哪种优惠更省钱
2.某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
优惠一:2700×0.9=2430元.
优惠二:200+2700×0.8=2360元.
答:选择优惠二更省钱.
优惠二:缴纳200元会费成为该超市一员,所有商品价格可获得八折优惠.
优惠一:非会员购物,所有商品价格可获九折优惠;
综合以上分类思考,可以发现:
当x<2000时,选择优惠一更省钱;
当x>2000时,选择优惠二更省钱.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
3.先分类讨论,再综合对比.
实际问题与
一元一次方程
(电话计费)
1.从多种信息表达形式中获取有关信息;
2.利用方程到关键点;
布置作业
教科书
第106页练习第2题;
第106页习题3.4第12题;
第111页复习题第10题.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
