14.1.1 同底数幂的乘法
文档属性
| 名称 | 14.1.1 同底数幂的乘法 |

|
|
| 格式 | zip | ||
| 文件大小 | 290.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-14 08:23:39 | ||
图片预览



文档简介
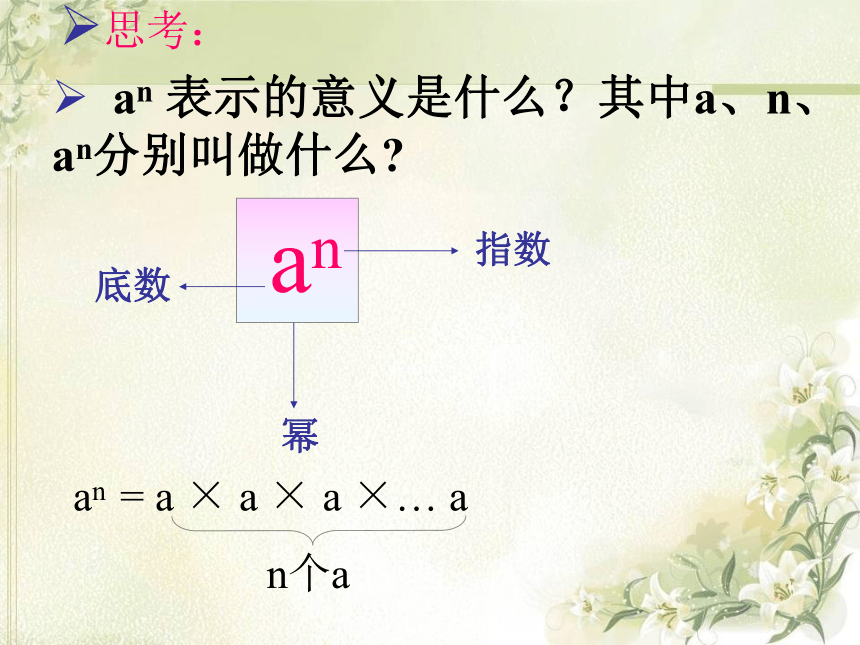
课件9张PPT。14.1.1 同底数幂的乘法南部县柳驿乡九年一贯制学校 宇 东 an 表示的意义是什么?其中a、n、an分别叫做什么? an底数幂指数思考:an = a × a × a ×… a
n个a
合作探究 23×24 = (2×2 ×2 ) ×( 2×2 ×2 ×2 )=2( ) (2) 53×54 = = 5( ) 7(5×5×5)×(5×5×5×5)7请同学们根据对乘方的意义的理解完成下列填空.(3)(-3)2×(-3)3 = = (-3)( )【(-3)×(-3)】×【(-3)×(-3)×(-3)】5(4)
= 4(5) a3×a4 = =a( )(a×a×a)×(a×a×a×a)7 结果与算式中的底数相同;结果中的指数等于算式中的指数和。
观察上面五个算式,你发现了什么?
am · an =m个an个a=aa………………………a=am+n(m+n)个a即:(aa…a)(aa…a)(乘方的意义)(乘法结合律)(乘方的意义)知识推导am · an = am+n (m、n都是正整数)同底数幂相乘, 底数不变, 指数相加。底数不变指数相加 同底数幂的乘法法则:(m,n为正整数)?(m,n,p为正整数)归纳探究一: 公式中的a可以表示那些数 (1) 计算: (2)(4) (3)探究二: 计算时应注意什么 1、 2、
已知:am=6, an=4.
求am+n =?.解: am+n = am · an
=6×4=24 探究三:公式还可以怎样用公式还可以逆用am+n = am · an 公式: am · an = am+n
(m、n都是正整数)小结同底数幂的乘法 法则 注意问题 运用公式时,底数a可以是数、单项式或多项式;同底数幂相乘,底数不变,指数相加。 三个或三个以上同底数幂相乘,法则也适用;公式可逆:am+n=am · an“指数相加”时不要忽略指数为1的因数;本节课你学到了什么?
n个a
合作探究 23×24 = (2×2 ×2 ) ×( 2×2 ×2 ×2 )=2( ) (2) 53×54 = = 5( ) 7(5×5×5)×(5×5×5×5)7请同学们根据对乘方的意义的理解完成下列填空.(3)(-3)2×(-3)3 = = (-3)( )【(-3)×(-3)】×【(-3)×(-3)×(-3)】5(4)
= 4(5) a3×a4 = =a( )(a×a×a)×(a×a×a×a)7 结果与算式中的底数相同;结果中的指数等于算式中的指数和。
观察上面五个算式,你发现了什么?
am · an =m个an个a=aa………………………a=am+n(m+n)个a即:(aa…a)(aa…a)(乘方的意义)(乘法结合律)(乘方的意义)知识推导am · an = am+n (m、n都是正整数)同底数幂相乘, 底数不变, 指数相加。底数不变指数相加 同底数幂的乘法法则:(m,n为正整数)?(m,n,p为正整数)归纳探究一: 公式中的a可以表示那些数 (1) 计算: (2)(4) (3)探究二: 计算时应注意什么 1、 2、
已知:am=6, an=4.
求am+n =?.解: am+n = am · an
=6×4=24 探究三:公式还可以怎样用公式还可以逆用am+n = am · an 公式: am · an = am+n
(m、n都是正整数)小结同底数幂的乘法 法则 注意问题 运用公式时,底数a可以是数、单项式或多项式;同底数幂相乘,底数不变,指数相加。 三个或三个以上同底数幂相乘,法则也适用;公式可逆:am+n=am · an“指数相加”时不要忽略指数为1的因数;本节课你学到了什么?
