人教版六年级上册数学《工程问题》教学方案(表格式)
文档属性
| 名称 | 人教版六年级上册数学《工程问题》教学方案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 14:53:24 | ||
图片预览

文档简介
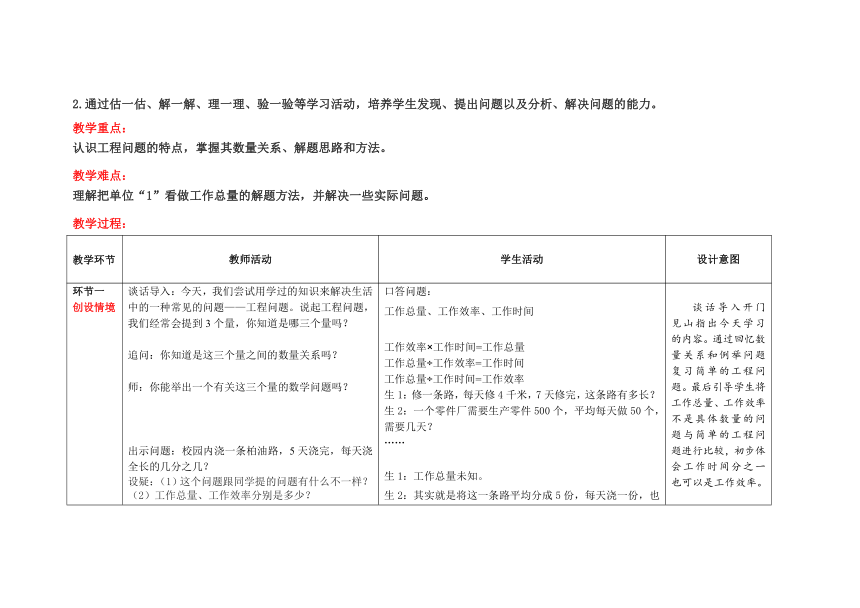
第三单元 分数除法
第8课时 工程问题
教学内容分析:
本课教材采用“工程问题”的素材,让学生经历自主探索、解决问题的过程,掌握假设、验证等方法解决问题的基本策略,让学生体会模型思想。对工作总量未知的问题,六年级的学生有解决简单工程问题的经验,能想到用“假设法”给予“工作总量”一个具体的数量,再利用工作总量÷工作效率=工作时间来解决问题。但是仅仅停留在此学生的思维并没有发生质的改变。因此本节课需要让学生通过对比观察能解释“为什么假设的道路全长不一样,但最终的工作时间都是相同的?”通过问题的讨论,借助线段图,在变化的量中找不变的量,即每天修的长度占总长度的几分之一是不变的。
教学目标:
1.让学生经历用“假设法”解决分数工程问题的过程,在对比观察中理解工作总量看作单位“1”的分数工程应用题的基本特点,掌握解题思路和解题方法。
2.通过估一估、解一解、理一理、验一验等学习活动,培养学生发现、提出问题以及分析、解决问题的能力。
教学重点:
认识工程问题的特点,掌握其数量关系、解题思路和方法。
教学难点:
理解把单位“1”看做工作总量的解题方法,并解决一些实际问题。
教学过程:
教学环节 教师活动 学生活动 设计意图
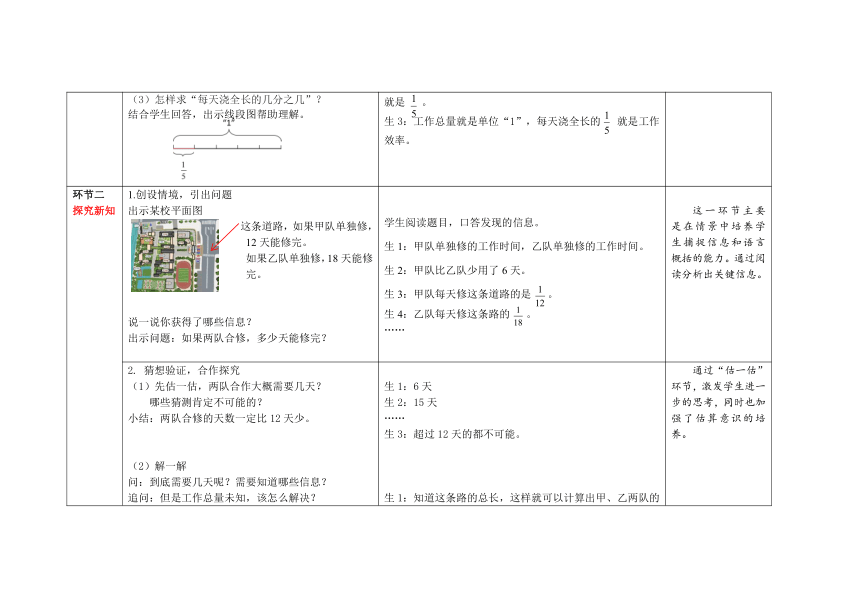
环节一 创设情境 谈话导入:今天,我们尝试用学过的知识来解决生活中的一种常见的问题——工程问题。说起工程问题,我们经常会提到3个量,你知道是哪三个量吗? 追问:你知道是这三个量之间的数量关系吗? 师:你能举出一个有关这三个量的数学问题吗? 出示问题:校园内浇一条柏油路,5天浇完,每天浇全长的几分之几? 设疑:(1)这个问题跟同学提的问题有什么不一样? (2)工作总量、工作效率分别是多少? (3)怎样求“每天浇全长的几分之几”? 结合学生回答,出示线段图帮助理解。 口答问题: 工作总量、工作效率、工作时间 工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间 工作总量÷工作时间=工作效率 生1:修一条路,每天修4千米,7天修完,这条路有多长? 生2:一个零件厂需要生产零件500个,平均每天做50个,需要几天? …… 生1:工作总量未知。 生2:其实就是将这一条路平均分成5份,每天浇一份,也就是 。 生3:工作总量就是单位“1”,每天浇全长的 就是工作效率。 谈话导入开门见山指出今天学习的内容。通过回忆数量关系和例举问题复习简单的工程问题。最后引导学生将工作总量、工作效率不是具体数量的问题与简单的工程问题进行比较,初步体会工作时间分之一也可以是工作效率。
环节二 探究新知 1.创设情境,引出问题 出示某校平面图 这条道路,如果甲队单独修, 12天能修完。 如果乙队单独修,18天能修完。 说一说你获得了哪些信息? 出示问题:如果两队合修,多少天能修完? 学生阅读题目,口答发现的信息。 生1:甲队单独修的工作时间,乙队单独修的工作时间。 生2:甲队比乙队少用了6天。 生3:甲队每天修这条道路的是 。 生4:乙队每天修这条路的 。 …… 这一环节主要是在情景中培养学生捕捉信息和语言概括的能力。通过阅读分析出关键信息。
猜想验证,合作探究 先估一估,两队合作大概需要几天? 哪些猜测肯定不可能的? 小结:两队合修的天数一定比12天少。 解一解 问:到底需要几天呢?需要知道哪些信息? 追问:但是工作总量未知,该怎么解决? 肯定过渡:假设法是解决问题中常用的一种办法。 请你假设一个道路全长的值,试着解一解。 反馈交流,说一说解题的思路和方法。 追问:假设全长100米可以吗? 结果还会是7.2天吗? 理一理 核心问题:假设的全长的长度不一样,为什么最后的时间都是7.2天? 根据学生回答出示线段图: 3.总结:不管这条是36米、72米还是100米,都可以看成一个整体,也就是单位“1”。这个单位“1”也就是工作总量,而两队合修的工作效率是( + ), 他们的工作效率之和不会随着长度的变化而发生变化。 说一说:对算式 的理解。 对比这么多的解法,你更喜欢哪一种? 生1:6天 生2:15天 …… 生3:超过12天的都不可能。 生1:知道这条路的总长,这样就可以计算出甲、乙两队的每天修的长度了。 生2:可以假设这条路全长是多少。 生独立解题。 生1:假设道路全长36米, 生2:假设道路全长72米, 生3:假设道路全长1米, …… 生:100米也可以,结果一定是7.2天。 生1:工作总量变大,相对应的工作效率也会增加,所以最后的时间还是不变的。 生2:工作时间应该和这条路的长短没有关系。因为甲队、乙队单独修的时间是不变的,那么他们的每天修的长度占全长的几分之几也是不变的。 生3:我也同意这样的想法。对这条路而言,他们每天修路的米数在变化,但他们每天修这条路的“几分之几”是没有变。 生:把这条路的工作总量看做“1”,他们的工作效率之和是( + ),工作总量除以工作效率就是工作时间了。 生1:假设36米,更容易理解。 生2:单位“1”的解法更简便。 通过“估一估”环节,激发学生进一步的思考,同时也加强了估算意识的培养。 解一解环节放手让学生独立解题,交流反馈时只要说的有理都给予肯定。尤其是对“1”的理解,不强化一定是单位“1”。 抓核心问题让学生深入思考。通过比较发现无论假设总长是多少,时间都是一样的。借助线段图帮助学生理解“变中不变”的本质。
4.回顾反思,验证对错 怎样验证刚才的解题过程是否正确? 生1:可以用数量关系工作效率×工作时间=工作总量来验证。 通过回顾与反思,让学生养成良好地解题习惯。
环节三 巩固练习 练习1:一批货物,只用甲车运,6次能运完;只用乙车运,3次能运完。如果两辆车一起运,多少次能运完这批货物? 独立完成,交流汇报 练习2:选一选 甲车从A城市到B城市要行驶8小时,乙车从B城市到A城市要行驶10小时。两车同时分别从A城市和B城市出发,几小时后相遇? 以上三种解法,哪些是正确的? 根据学生回答,分析B选项的问题。 练习3:练一练 一批零件,如果王师傅单独加工,需要10天;如果李师傅单独加工,需要15天。王师傅和李师傅合作,多少天能加工这批零件的 。 仔细阅读题目,说一说这个问题有什么不一样? 追问:工作总量发生了变化,你能用今天学过的知识解决这一问题吗? 反馈交流,说一说解题思路和方法。 还有不同的解法吗? 总结:可以先计算出工作总量的 ,也可以先计算出总的工作时间,再计算总工作时间的 。 生1:假设有6吨货物,那么 。 生2:这批货物就是单位“1”,那么 。 学生独立思考后手势判断。 C正确,B 错误。 生:B选项是假设AB两地之间的距离为40千米,那么甲车的速度应该是40÷8,乙车的速度是40÷8,所以B选项是错误的。 生:工作总量不是“1”,只需完成 。 生1:假设这批零件有300个。 生2: 300× =200(个) 200÷(200÷10 +200÷15) =200÷50 =4(天) 生3: 此题是采用运货的素材使学生感受与工程问题的相同性,巩固假设法解决此类问题。 为避免学生对知识的理解产生片面性,此题通过辨析,让学生进一步明确工作总量和工作效率必须要对应,促使学生对工程问题本质特征的理解。 通过变式练习,引导学生寻找知识间的联系,进行迁移、类推,有效巩固工程问题的解题思路和解题方法。通过反馈和追问不用的解法,激发学生从不同思路思考问题,拓宽学生的思维。
环节四 课堂小结 你有什么收获? 小结工程问题的特点及解题方法。 回顾本节课自己的体会和收获。 可以用假设法解答。 可以用单位“1”表示工作总量,表示工作效率来解答。 引导学生回顾本节课的学习过程,再次巩固工程问题的数学模型。
环节五 布置作业 教材P42第7题,P43第8题、第9题。
第8课时 工程问题
教学内容分析:
本课教材采用“工程问题”的素材,让学生经历自主探索、解决问题的过程,掌握假设、验证等方法解决问题的基本策略,让学生体会模型思想。对工作总量未知的问题,六年级的学生有解决简单工程问题的经验,能想到用“假设法”给予“工作总量”一个具体的数量,再利用工作总量÷工作效率=工作时间来解决问题。但是仅仅停留在此学生的思维并没有发生质的改变。因此本节课需要让学生通过对比观察能解释“为什么假设的道路全长不一样,但最终的工作时间都是相同的?”通过问题的讨论,借助线段图,在变化的量中找不变的量,即每天修的长度占总长度的几分之一是不变的。
教学目标:
1.让学生经历用“假设法”解决分数工程问题的过程,在对比观察中理解工作总量看作单位“1”的分数工程应用题的基本特点,掌握解题思路和解题方法。
2.通过估一估、解一解、理一理、验一验等学习活动,培养学生发现、提出问题以及分析、解决问题的能力。
教学重点:
认识工程问题的特点,掌握其数量关系、解题思路和方法。
教学难点:
理解把单位“1”看做工作总量的解题方法,并解决一些实际问题。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 谈话导入:今天,我们尝试用学过的知识来解决生活中的一种常见的问题——工程问题。说起工程问题,我们经常会提到3个量,你知道是哪三个量吗? 追问:你知道是这三个量之间的数量关系吗? 师:你能举出一个有关这三个量的数学问题吗? 出示问题:校园内浇一条柏油路,5天浇完,每天浇全长的几分之几? 设疑:(1)这个问题跟同学提的问题有什么不一样? (2)工作总量、工作效率分别是多少? (3)怎样求“每天浇全长的几分之几”? 结合学生回答,出示线段图帮助理解。 口答问题: 工作总量、工作效率、工作时间 工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间 工作总量÷工作时间=工作效率 生1:修一条路,每天修4千米,7天修完,这条路有多长? 生2:一个零件厂需要生产零件500个,平均每天做50个,需要几天? …… 生1:工作总量未知。 生2:其实就是将这一条路平均分成5份,每天浇一份,也就是 。 生3:工作总量就是单位“1”,每天浇全长的 就是工作效率。 谈话导入开门见山指出今天学习的内容。通过回忆数量关系和例举问题复习简单的工程问题。最后引导学生将工作总量、工作效率不是具体数量的问题与简单的工程问题进行比较,初步体会工作时间分之一也可以是工作效率。
环节二 探究新知 1.创设情境,引出问题 出示某校平面图 这条道路,如果甲队单独修, 12天能修完。 如果乙队单独修,18天能修完。 说一说你获得了哪些信息? 出示问题:如果两队合修,多少天能修完? 学生阅读题目,口答发现的信息。 生1:甲队单独修的工作时间,乙队单独修的工作时间。 生2:甲队比乙队少用了6天。 生3:甲队每天修这条道路的是 。 生4:乙队每天修这条路的 。 …… 这一环节主要是在情景中培养学生捕捉信息和语言概括的能力。通过阅读分析出关键信息。
猜想验证,合作探究 先估一估,两队合作大概需要几天? 哪些猜测肯定不可能的? 小结:两队合修的天数一定比12天少。 解一解 问:到底需要几天呢?需要知道哪些信息? 追问:但是工作总量未知,该怎么解决? 肯定过渡:假设法是解决问题中常用的一种办法。 请你假设一个道路全长的值,试着解一解。 反馈交流,说一说解题的思路和方法。 追问:假设全长100米可以吗? 结果还会是7.2天吗? 理一理 核心问题:假设的全长的长度不一样,为什么最后的时间都是7.2天? 根据学生回答出示线段图: 3.总结:不管这条是36米、72米还是100米,都可以看成一个整体,也就是单位“1”。这个单位“1”也就是工作总量,而两队合修的工作效率是( + ), 他们的工作效率之和不会随着长度的变化而发生变化。 说一说:对算式 的理解。 对比这么多的解法,你更喜欢哪一种? 生1:6天 生2:15天 …… 生3:超过12天的都不可能。 生1:知道这条路的总长,这样就可以计算出甲、乙两队的每天修的长度了。 生2:可以假设这条路全长是多少。 生独立解题。 生1:假设道路全长36米, 生2:假设道路全长72米, 生3:假设道路全长1米, …… 生:100米也可以,结果一定是7.2天。 生1:工作总量变大,相对应的工作效率也会增加,所以最后的时间还是不变的。 生2:工作时间应该和这条路的长短没有关系。因为甲队、乙队单独修的时间是不变的,那么他们的每天修的长度占全长的几分之几也是不变的。 生3:我也同意这样的想法。对这条路而言,他们每天修路的米数在变化,但他们每天修这条路的“几分之几”是没有变。 生:把这条路的工作总量看做“1”,他们的工作效率之和是( + ),工作总量除以工作效率就是工作时间了。 生1:假设36米,更容易理解。 生2:单位“1”的解法更简便。 通过“估一估”环节,激发学生进一步的思考,同时也加强了估算意识的培养。 解一解环节放手让学生独立解题,交流反馈时只要说的有理都给予肯定。尤其是对“1”的理解,不强化一定是单位“1”。 抓核心问题让学生深入思考。通过比较发现无论假设总长是多少,时间都是一样的。借助线段图帮助学生理解“变中不变”的本质。
4.回顾反思,验证对错 怎样验证刚才的解题过程是否正确? 生1:可以用数量关系工作效率×工作时间=工作总量来验证。 通过回顾与反思,让学生养成良好地解题习惯。
环节三 巩固练习 练习1:一批货物,只用甲车运,6次能运完;只用乙车运,3次能运完。如果两辆车一起运,多少次能运完这批货物? 独立完成,交流汇报 练习2:选一选 甲车从A城市到B城市要行驶8小时,乙车从B城市到A城市要行驶10小时。两车同时分别从A城市和B城市出发,几小时后相遇? 以上三种解法,哪些是正确的? 根据学生回答,分析B选项的问题。 练习3:练一练 一批零件,如果王师傅单独加工,需要10天;如果李师傅单独加工,需要15天。王师傅和李师傅合作,多少天能加工这批零件的 。 仔细阅读题目,说一说这个问题有什么不一样? 追问:工作总量发生了变化,你能用今天学过的知识解决这一问题吗? 反馈交流,说一说解题思路和方法。 还有不同的解法吗? 总结:可以先计算出工作总量的 ,也可以先计算出总的工作时间,再计算总工作时间的 。 生1:假设有6吨货物,那么 。 生2:这批货物就是单位“1”,那么 。 学生独立思考后手势判断。 C正确,B 错误。 生:B选项是假设AB两地之间的距离为40千米,那么甲车的速度应该是40÷8,乙车的速度是40÷8,所以B选项是错误的。 生:工作总量不是“1”,只需完成 。 生1:假设这批零件有300个。 生2: 300× =200(个) 200÷(200÷10 +200÷15) =200÷50 =4(天) 生3: 此题是采用运货的素材使学生感受与工程问题的相同性,巩固假设法解决此类问题。 为避免学生对知识的理解产生片面性,此题通过辨析,让学生进一步明确工作总量和工作效率必须要对应,促使学生对工程问题本质特征的理解。 通过变式练习,引导学生寻找知识间的联系,进行迁移、类推,有效巩固工程问题的解题思路和解题方法。通过反馈和追问不用的解法,激发学生从不同思路思考问题,拓宽学生的思维。
环节四 课堂小结 你有什么收获? 小结工程问题的特点及解题方法。 回顾本节课自己的体会和收获。 可以用假设法解答。 可以用单位“1”表示工作总量,表示工作效率来解答。 引导学生回顾本节课的学习过程,再次巩固工程问题的数学模型。
环节五 布置作业 教材P42第7题,P43第8题、第9题。
