人教版六年级上册数学《分数求和问题》教学方案(表格式)
文档属性
| 名称 | 人教版六年级上册数学《分数求和问题》教学方案(表格式) | 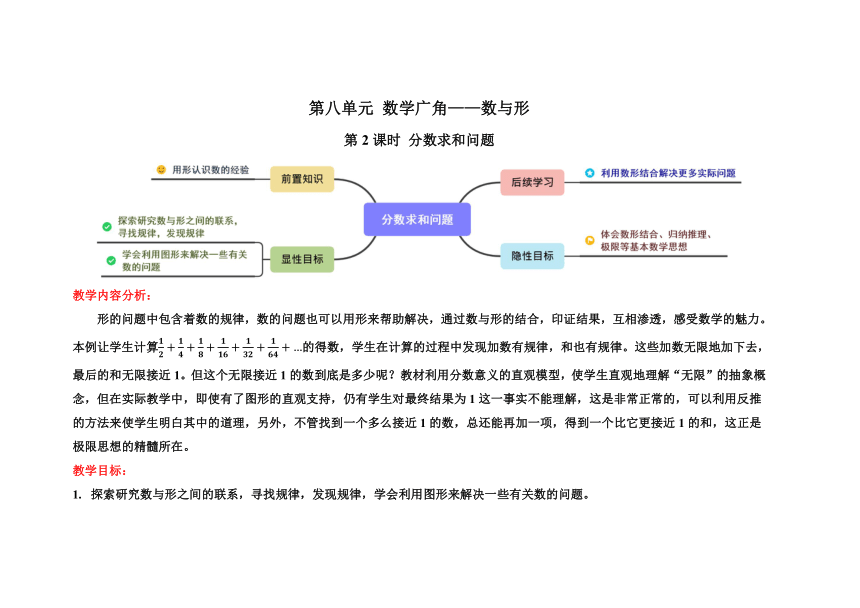 | |
| 格式 | docx | ||
| 文件大小 | 181.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 14:54:20 | ||
图片预览

文档简介
第八单元 数学广角——数与形
第2课时 分数求和问题
教学内容分析:
形的问题中包含着数的规律,数的问题也可以用形来帮助解决,通过数与形的结合,印证结果,互相渗透,感受数学的魅力。本例让学生计算的得数,学生在计算的过程中发现加数有规律,和也有规律。这些加数无限地加下去,最后的和无限接近1。但这个无限接近1的数到底是多少呢?教材利用分数意义的直观模型,使学生直观地理解“无限”的抽象概念,但在实际教学中,即使有了图形的直观支持,仍有学生对最终结果为1这一事实不能理解,这是非常正常的,可以利用反推的方法来使学生明白其中的道理,另外,不管找到一个多么接近1的数,总还能再加一项,得到一个比它更接近1的和,这正是极限思想的精髓所在。
教学目标:
探索研究数与形之间的联系,寻找规律,发现规律,学会利用图形来解决一些有关数的问题。
让学生经历猜想与验证的过程,体会数形结合、归纳推理、极限等基本数学思想。
教学重点:
在数与形之间建立联系,发现规律,利用图形来解决有关数的问题。
教学难点:
积累数学活动经验,经历猜想与验证的探索过程。
教学过程:
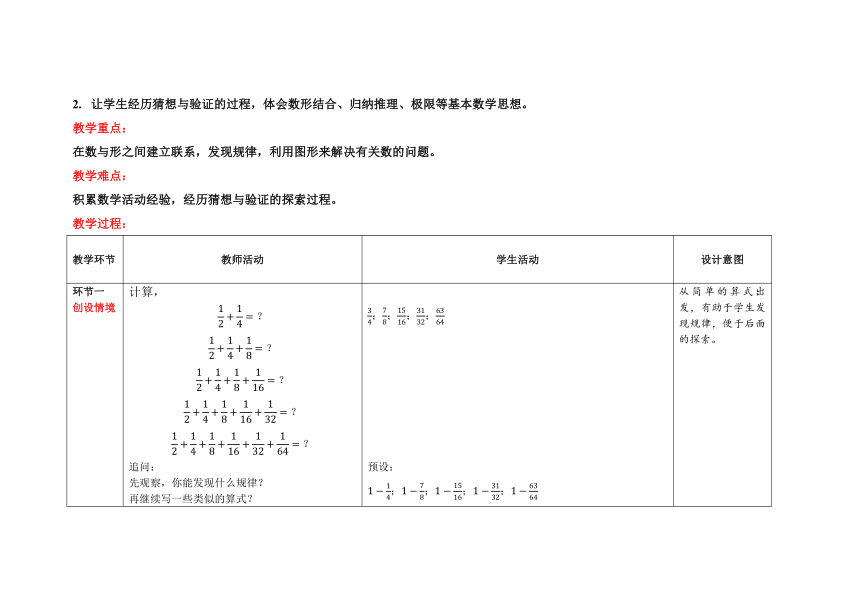
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 计算, 追问: 先观察,你能发现什么规律? 再继续写一些类似的算式? ;;;; 预设: ;;;; 加数的规律:分子是1,分母依次扩大2倍。 和的规律:用1减去最后这个几分之一就可以得到答案了。 从简单的算式出发,有助于学生发现规律,便于后面的探索。
环节二 探究新知 1.从有限个加数相加过渡到无数个加数相加 思考:如果按上面的规律一直加下去,结果是多少呢?省略号是什么意思? 说一说,你是怎样想的,你有什么发现? 预设:省略号表示后边还有很多数,无数个。 从有限个加数相加过渡到无数个加数相加,激发学生的认知冲突,初步感受无限。
2.经历探索过程,猜想结果 提示:从数的角度思考;从形的角度观察。 追问: 如果继续往下加,下一个数加在哪里? 学生交流想法,对结果进行猜测。 从数的角度思考 预设:得数的分子与分母越来越大,说明等分的份数越来越多,取得份数也越来越多,分子比分母只少了一份,算式的结果越来越接近于1。猜测。 从形的角度观察 先通过平分找到图形的,然后在的基础上继续平分,加上、、、、。 预设: 加在空白部分。算式的意思就是在空白处不停地加下去。 如果继续往下加,所有的扇形(或长方形、线段)会把整个圆(或正方形、线段)占满。猜测这些数相加之和为1。 学生能感受到结果接近1,但是这个无限接近1的数到底是多少呢?探究过程中,鼓励学生多角度思考,借助图形进行推理,又能够从数的角度进行验证。 进一步感受极限思想,通过反推,进行验证。
3.反推验证 谈话:既然结果和1有关,我们就从1开始想。 继续将第二个分成,像这样一层一层分下去,试着分一分,想一想,说说你的发现。 预设:,分不完,能分无数个。
4.再次感受极限,加深理解 1-0.9= 1-0.99= 1-0.999= 1-0.9999= 1-0.99999= 1-0.999999= 1-0.999…= 0.1;0.01;0.001;0.0001;0.00001;0.000001 1=0.999… 预设:随着小数部分9的个数的不断增多,与1的差在逐渐的减少,而在0.999…中的小数部分有无数个9,发现差会越来越小,最终为0,从而1=0.999…。 再次感受极限,加深对极限思想的理解与认识。
环节三 巩固新知 利用画图解决代数问题,体会图示的直观性。 学生借助图示,通过推理,建立形和数之间的联系从而解决实际问题。 通过连线法,解决逻辑推理问题,既直观又便捷。 学生通过解决不同层次的问题,体会数形结合的直观与便捷。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 布置作业 教材P110练习二十三第5、8题。
第2课时 分数求和问题
教学内容分析:
形的问题中包含着数的规律,数的问题也可以用形来帮助解决,通过数与形的结合,印证结果,互相渗透,感受数学的魅力。本例让学生计算的得数,学生在计算的过程中发现加数有规律,和也有规律。这些加数无限地加下去,最后的和无限接近1。但这个无限接近1的数到底是多少呢?教材利用分数意义的直观模型,使学生直观地理解“无限”的抽象概念,但在实际教学中,即使有了图形的直观支持,仍有学生对最终结果为1这一事实不能理解,这是非常正常的,可以利用反推的方法来使学生明白其中的道理,另外,不管找到一个多么接近1的数,总还能再加一项,得到一个比它更接近1的和,这正是极限思想的精髓所在。
教学目标:
探索研究数与形之间的联系,寻找规律,发现规律,学会利用图形来解决一些有关数的问题。
让学生经历猜想与验证的过程,体会数形结合、归纳推理、极限等基本数学思想。
教学重点:
在数与形之间建立联系,发现规律,利用图形来解决有关数的问题。
教学难点:
积累数学活动经验,经历猜想与验证的探索过程。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 计算, 追问: 先观察,你能发现什么规律? 再继续写一些类似的算式? ;;;; 预设: ;;;; 加数的规律:分子是1,分母依次扩大2倍。 和的规律:用1减去最后这个几分之一就可以得到答案了。 从简单的算式出发,有助于学生发现规律,便于后面的探索。
环节二 探究新知 1.从有限个加数相加过渡到无数个加数相加 思考:如果按上面的规律一直加下去,结果是多少呢?省略号是什么意思? 说一说,你是怎样想的,你有什么发现? 预设:省略号表示后边还有很多数,无数个。 从有限个加数相加过渡到无数个加数相加,激发学生的认知冲突,初步感受无限。
2.经历探索过程,猜想结果 提示:从数的角度思考;从形的角度观察。 追问: 如果继续往下加,下一个数加在哪里? 学生交流想法,对结果进行猜测。 从数的角度思考 预设:得数的分子与分母越来越大,说明等分的份数越来越多,取得份数也越来越多,分子比分母只少了一份,算式的结果越来越接近于1。猜测。 从形的角度观察 先通过平分找到图形的,然后在的基础上继续平分,加上、、、、。 预设: 加在空白部分。算式的意思就是在空白处不停地加下去。 如果继续往下加,所有的扇形(或长方形、线段)会把整个圆(或正方形、线段)占满。猜测这些数相加之和为1。 学生能感受到结果接近1,但是这个无限接近1的数到底是多少呢?探究过程中,鼓励学生多角度思考,借助图形进行推理,又能够从数的角度进行验证。 进一步感受极限思想,通过反推,进行验证。
3.反推验证 谈话:既然结果和1有关,我们就从1开始想。 继续将第二个分成,像这样一层一层分下去,试着分一分,想一想,说说你的发现。 预设:,分不完,能分无数个。
4.再次感受极限,加深理解 1-0.9= 1-0.99= 1-0.999= 1-0.9999= 1-0.99999= 1-0.999999= 1-0.999…= 0.1;0.01;0.001;0.0001;0.00001;0.000001 1=0.999… 预设:随着小数部分9的个数的不断增多,与1的差在逐渐的减少,而在0.999…中的小数部分有无数个9,发现差会越来越小,最终为0,从而1=0.999…。 再次感受极限,加深对极限思想的理解与认识。
环节三 巩固新知 利用画图解决代数问题,体会图示的直观性。 学生借助图示,通过推理,建立形和数之间的联系从而解决实际问题。 通过连线法,解决逻辑推理问题,既直观又便捷。 学生通过解决不同层次的问题,体会数形结合的直观与便捷。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 鼓励学生畅谈自己的收获和体会,有哪些认知上的冲突,遇到问题是如何解决的。
环节五 布置作业 教材P110练习二十三第5、8题。
