人教版六年级上册数学《扇形》教学方案(表格式)
文档属性
| 名称 | 人教版六年级上册数学《扇形》教学方案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 370.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览



文档简介
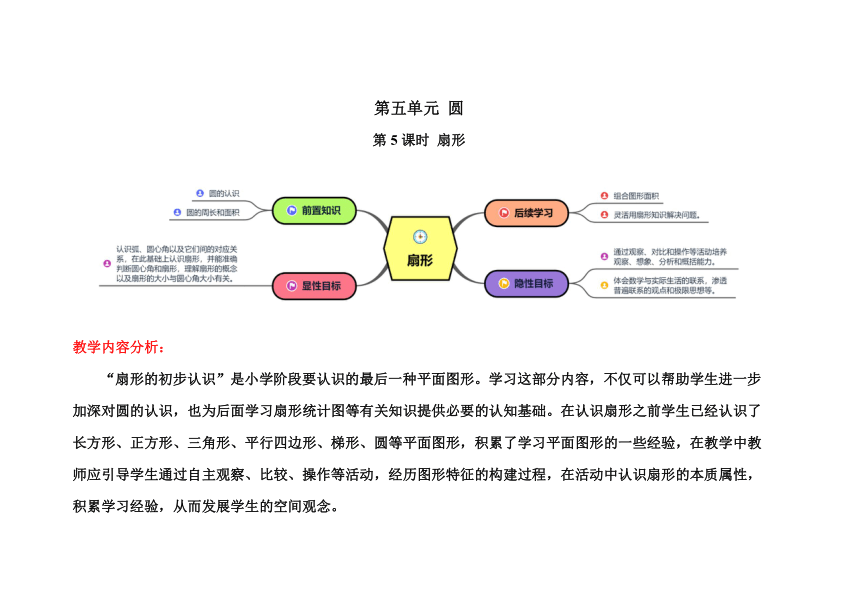
第五单元 圆
第5课时 扇形
教学内容分析:
“扇形的初步认识”是小学阶段要认识的最后一种平面图形。学习这部分内容,不仅可以帮助学生进一步加深对圆的认识,也为后面学习扇形统计图等有关知识提供必要的认知基础。在认识扇形之前学生已经认识了长方形、正方形、三角形、平行四边形、梯形、圆等平面图形,积累了学习平面图形的一些经验,在教学中教师应引导学生通过自主观察、比较、操作等活动,经历图形特征的构建过程,在活动中认识扇形的本质属性,积累学习经验,从而发展学生的空间观念。
教学目标:
1.认识弧、圆心角以及它们间的对应关系,在此基础上认识扇形,并能准确判断圆心角和扇形,理解扇形的概念以及扇形的大小与圆心角大小有关。
2.通过观察、对比和操作等活动培养观察、想象、分析和概括能力。
教学重点:
认识弧、圆心角、扇形,能准确判断扇形。
教学难点:
理解扇形的大小与圆心角大小有关。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 欣赏扇子 扇子起源于中国,在中国已有3000多年历史,让我们一起来欣赏美丽的扇子吧! 同学们,像这样打开扇子,就能得到这样的一些形状(课件演示:描出扇子轮廓,隐去实物图),知道它们是什么图形吗? 揭题:今天我们就一起来认识扇形。 学生欣赏图片。 学生回答:扇形。 由生活中的折扇引入并抽象出扇形,能有效唤醒学生认识图形的已有经验,激发他们对扇形的兴趣。同时扇子不断打开的过程,能自然而然地将圆和扇形联系起来,有助于学生初步感知要学习的扇形与圆的联系。
环节二 探究新知 1.观察辨析,认识特征 提问:想象一下,如果把折扇继续打开,会得到什么图形? 如果把折扇的边旋转一周,最终会得到什么图形? 追问:那扇形和圆之间有什么联系呢?我们不妨把这些扇形放到圆形中来观察,你能发现它们有哪些共同的特点? 小结:像这样在圆上定两点,两点之间的曲线叫做弧。扇形的两条半径组成一个角,它的顶点是圆心,像这样顶点在圆心的角叫做圆心角。这条弧就是这个圆心角所对的弧;弧和圆心角正好相对。一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。 指一指:请你指出这两个扇形中每个圆心角以及所对的弧。 学生回答: 扇形 圆 ①扇形中有两条线段,它们都是圆的半径; ②还有一条曲线,这条曲线在圆上; 引导学生主动开展观察、操作、比较、抽象等活动,从形状特征、构成要素、与圆的关系等多方面对扇形的特征获得感知,完成对概念的抽象,逐步完善对扇形的认识,积累思维活动的经验。
2.强化练习,突显特征 (1)下列图形中哪些角是圆心角? 说说你的理由! 变式练习 仔细观察,下面这个图形是扇形吗?说说你的理由! 引导:要判断是不是扇形,可以从扇形的构成要素来判断(出示圆),现在你能判断了吗? 结论:上面的图形,虽然角的顶点在圆心,角的两条边是圆的半径,但曲线并不是圆心角所对应的弧,所以它不是扇形。 学生回答: 第1和第4幅图是圆心角,因为它们都是由一条弧和经过弧的两个端点的半径围成的。 第2和第3幅图中角的顶点不在圆心上,不是圆心角。 ①是扇形,因为这个图形是两条线段和一条弧围成的。 ②这个图形看上去是圆的一部分,肯定是扇形。 学生回答: 不是扇形。 和其他平面图形不同,认识扇形不仅要弄清扇形的构成要素,还要理解扇形与所在圆的关系。为此,设计了两个层次的活动,首先呈现了四个图形,通过正例和反例的观察、比较和判断,帮助学生理解构成扇形的必要条件;其次是变式练习,所呈现的例子具有一定的迷惑性,通过辨析能更好地帮助学生理解扇形与所在圆之间的关系,领悟概念的本质。
3.动手操作,深化认识 (1)提问:猜一猜,扇形大小和它的什么有关? (2)制作扇形,并验证扇形大小和它的半径有关 四人小组合作验证,要求:先想想怎么制作扇形能验证扇形大小和半径、圆心角有关,再动手做扇形。 交流反馈 说说你们是怎么验证的? 看来,当圆心角相同时,半径的大小决定扇形大小。 看来,当半径相同时,也就是在同一个圆中,圆心角越大,弧越长;圆心角越小,弧越短。大家的猜想没错,扇形大小和它的圆心角、半径有关。 计算圆心角大小 我们的生活中也有很多的扇形,请看钟面上,分针从12起走5分钟,所经过的部分就是个扇形,你知道它的圆心角是几度吗? 那么分针继续转,从12转到3,转到6,转35分分别是几度?请你算一算。 反馈交流 追部:第三幅的空白部分扇形圆心角是多少度? 学生回答: ①和它的半径有关;②和它的圆心角有关。 四人小组动手操作。 学生回答: ①我们画了3个半径不同的圆,在圆内画出圆心角相等的扇形,发现半径越大,扇形越大,半径越小,扇形越小。 ②我们画了3个半径相同的圆,在圆内画出圆心角不同的扇形,发现圆心角越大,扇形越大,圆心角越小,扇形越小。 学生回答: 周角是360度,钟面上有12大格,所以每个大格是360÷12=30度。所以这个扇形的圆心角是30度。 学生独立完成。 分针从12转到3 ,圆心角是3个30度,即90度,是直角;转到6,圆心角是6个30度是180度,是个平角,转35分也就是7大格,是210度。 空白部分有5格,圆心角是150度。 观察和操作是小学生认识和研究图形特征的重要方式。本环节,先让学生自己动手做扇形,在制作比较的过程中感受扇形的大小与圆心角、半径之间的关系。意图调动学生的视觉、听觉、触觉等多种感官,使他们在参与活动的过程中自主发现、自主理解、自我体验,进而 丰富对扇形的认识,积累数学活动经验。
环节三 巩固练习 画一个半径是2cm的圆,再在圆中画一个圆心角是120°的扇形。 完成后反馈。 2.求扇形的周长和面积。 完成后反馈。 3.解决问题。 做这把扇子,需要用多少布料? 学生独立完成。 学生独立完成。 弧长=圆周长÷4 2×4×3.14÷4 =2×3.14 =6.28(cm) 扇形周长=弧长+2×半径 6.28+2×4=14.28(cm) 扇形面积=圆面积÷4 3.14×4×4÷4 =3.14×4 =12.56(cm2) S大半圆=S大圆÷2 3.14×(40÷2)2÷2 =3.14×200 =628(cm2) S小半圆=S小圆÷2 3.14×(16÷2)2÷2 = 3.14×32 =100.48(cm2) 布料面积=628-100.48=527.52(cm2) 答:需要用527.52平方厘米的布料。 以画扇形来巩固对扇形概念的理解。 利用扇形与圆之间的关系,求扇形周长和面积,将学到的知识灵活运用。 用今天学到的知识解决生活中的实际问题,同时引导灵活运用扇形解决扇环问题。
环节四 课堂小结 你有什么收获? 我知道了什么是扇形,以及扇形各部分名称,知道了怎么计算圆心角。 鼓励学生畅谈自己的收获和体会。
环节五 布置作业 教材P76第1、2、4题。
第5课时 扇形
教学内容分析:
“扇形的初步认识”是小学阶段要认识的最后一种平面图形。学习这部分内容,不仅可以帮助学生进一步加深对圆的认识,也为后面学习扇形统计图等有关知识提供必要的认知基础。在认识扇形之前学生已经认识了长方形、正方形、三角形、平行四边形、梯形、圆等平面图形,积累了学习平面图形的一些经验,在教学中教师应引导学生通过自主观察、比较、操作等活动,经历图形特征的构建过程,在活动中认识扇形的本质属性,积累学习经验,从而发展学生的空间观念。
教学目标:
1.认识弧、圆心角以及它们间的对应关系,在此基础上认识扇形,并能准确判断圆心角和扇形,理解扇形的概念以及扇形的大小与圆心角大小有关。
2.通过观察、对比和操作等活动培养观察、想象、分析和概括能力。
教学重点:
认识弧、圆心角、扇形,能准确判断扇形。
教学难点:
理解扇形的大小与圆心角大小有关。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 欣赏扇子 扇子起源于中国,在中国已有3000多年历史,让我们一起来欣赏美丽的扇子吧! 同学们,像这样打开扇子,就能得到这样的一些形状(课件演示:描出扇子轮廓,隐去实物图),知道它们是什么图形吗? 揭题:今天我们就一起来认识扇形。 学生欣赏图片。 学生回答:扇形。 由生活中的折扇引入并抽象出扇形,能有效唤醒学生认识图形的已有经验,激发他们对扇形的兴趣。同时扇子不断打开的过程,能自然而然地将圆和扇形联系起来,有助于学生初步感知要学习的扇形与圆的联系。
环节二 探究新知 1.观察辨析,认识特征 提问:想象一下,如果把折扇继续打开,会得到什么图形? 如果把折扇的边旋转一周,最终会得到什么图形? 追问:那扇形和圆之间有什么联系呢?我们不妨把这些扇形放到圆形中来观察,你能发现它们有哪些共同的特点? 小结:像这样在圆上定两点,两点之间的曲线叫做弧。扇形的两条半径组成一个角,它的顶点是圆心,像这样顶点在圆心的角叫做圆心角。这条弧就是这个圆心角所对的弧;弧和圆心角正好相对。一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。 指一指:请你指出这两个扇形中每个圆心角以及所对的弧。 学生回答: 扇形 圆 ①扇形中有两条线段,它们都是圆的半径; ②还有一条曲线,这条曲线在圆上; 引导学生主动开展观察、操作、比较、抽象等活动,从形状特征、构成要素、与圆的关系等多方面对扇形的特征获得感知,完成对概念的抽象,逐步完善对扇形的认识,积累思维活动的经验。
2.强化练习,突显特征 (1)下列图形中哪些角是圆心角? 说说你的理由! 变式练习 仔细观察,下面这个图形是扇形吗?说说你的理由! 引导:要判断是不是扇形,可以从扇形的构成要素来判断(出示圆),现在你能判断了吗? 结论:上面的图形,虽然角的顶点在圆心,角的两条边是圆的半径,但曲线并不是圆心角所对应的弧,所以它不是扇形。 学生回答: 第1和第4幅图是圆心角,因为它们都是由一条弧和经过弧的两个端点的半径围成的。 第2和第3幅图中角的顶点不在圆心上,不是圆心角。 ①是扇形,因为这个图形是两条线段和一条弧围成的。 ②这个图形看上去是圆的一部分,肯定是扇形。 学生回答: 不是扇形。 和其他平面图形不同,认识扇形不仅要弄清扇形的构成要素,还要理解扇形与所在圆的关系。为此,设计了两个层次的活动,首先呈现了四个图形,通过正例和反例的观察、比较和判断,帮助学生理解构成扇形的必要条件;其次是变式练习,所呈现的例子具有一定的迷惑性,通过辨析能更好地帮助学生理解扇形与所在圆之间的关系,领悟概念的本质。
3.动手操作,深化认识 (1)提问:猜一猜,扇形大小和它的什么有关? (2)制作扇形,并验证扇形大小和它的半径有关 四人小组合作验证,要求:先想想怎么制作扇形能验证扇形大小和半径、圆心角有关,再动手做扇形。 交流反馈 说说你们是怎么验证的? 看来,当圆心角相同时,半径的大小决定扇形大小。 看来,当半径相同时,也就是在同一个圆中,圆心角越大,弧越长;圆心角越小,弧越短。大家的猜想没错,扇形大小和它的圆心角、半径有关。 计算圆心角大小 我们的生活中也有很多的扇形,请看钟面上,分针从12起走5分钟,所经过的部分就是个扇形,你知道它的圆心角是几度吗? 那么分针继续转,从12转到3,转到6,转35分分别是几度?请你算一算。 反馈交流 追部:第三幅的空白部分扇形圆心角是多少度? 学生回答: ①和它的半径有关;②和它的圆心角有关。 四人小组动手操作。 学生回答: ①我们画了3个半径不同的圆,在圆内画出圆心角相等的扇形,发现半径越大,扇形越大,半径越小,扇形越小。 ②我们画了3个半径相同的圆,在圆内画出圆心角不同的扇形,发现圆心角越大,扇形越大,圆心角越小,扇形越小。 学生回答: 周角是360度,钟面上有12大格,所以每个大格是360÷12=30度。所以这个扇形的圆心角是30度。 学生独立完成。 分针从12转到3 ,圆心角是3个30度,即90度,是直角;转到6,圆心角是6个30度是180度,是个平角,转35分也就是7大格,是210度。 空白部分有5格,圆心角是150度。 观察和操作是小学生认识和研究图形特征的重要方式。本环节,先让学生自己动手做扇形,在制作比较的过程中感受扇形的大小与圆心角、半径之间的关系。意图调动学生的视觉、听觉、触觉等多种感官,使他们在参与活动的过程中自主发现、自主理解、自我体验,进而 丰富对扇形的认识,积累数学活动经验。
环节三 巩固练习 画一个半径是2cm的圆,再在圆中画一个圆心角是120°的扇形。 完成后反馈。 2.求扇形的周长和面积。 完成后反馈。 3.解决问题。 做这把扇子,需要用多少布料? 学生独立完成。 学生独立完成。 弧长=圆周长÷4 2×4×3.14÷4 =2×3.14 =6.28(cm) 扇形周长=弧长+2×半径 6.28+2×4=14.28(cm) 扇形面积=圆面积÷4 3.14×4×4÷4 =3.14×4 =12.56(cm2) S大半圆=S大圆÷2 3.14×(40÷2)2÷2 =3.14×200 =628(cm2) S小半圆=S小圆÷2 3.14×(16÷2)2÷2 = 3.14×32 =100.48(cm2) 布料面积=628-100.48=527.52(cm2) 答:需要用527.52平方厘米的布料。 以画扇形来巩固对扇形概念的理解。 利用扇形与圆之间的关系,求扇形周长和面积,将学到的知识灵活运用。 用今天学到的知识解决生活中的实际问题,同时引导灵活运用扇形解决扇环问题。
环节四 课堂小结 你有什么收获? 我知道了什么是扇形,以及扇形各部分名称,知道了怎么计算圆心角。 鼓励学生畅谈自己的收获和体会。
环节五 布置作业 教材P76第1、2、4题。
