13.1全等三角形[上学期]
文档属性
| 名称 | 13.1全等三角形[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 736.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-29 00:00:00 | ||
图片预览




文档简介
课件24张PPT。数学是思维的体操
数学是思维的修炼
数学是思维的艺术
数学是智力的阶梯全等三角形同一张底片洗出的照片是
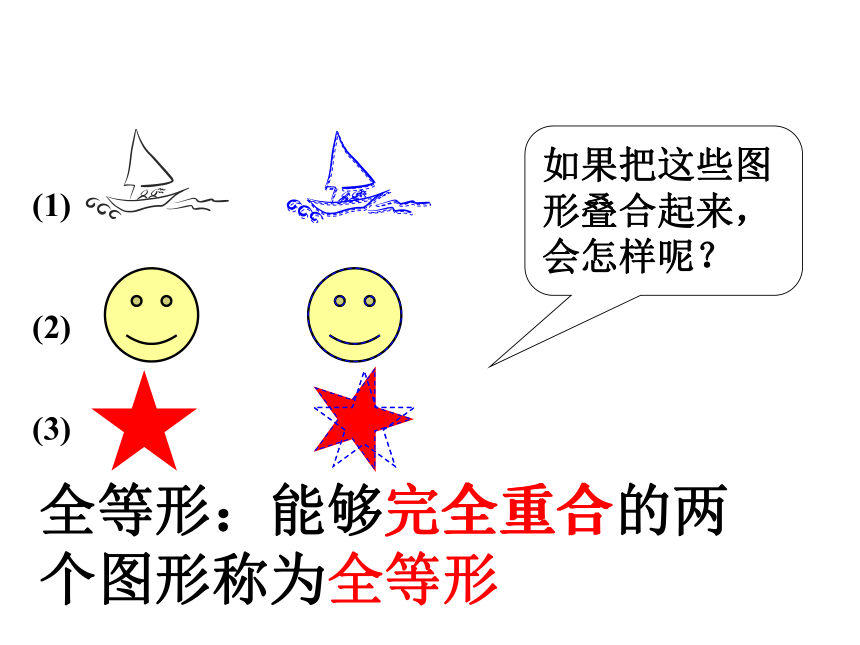
能够完全重合的(1)(2)(3)全等形:能够完全重合的两 个图形称为全等形如果把这些图形叠合起来,会怎样呢?完全重合3.两个全等的三角形完全重合时,
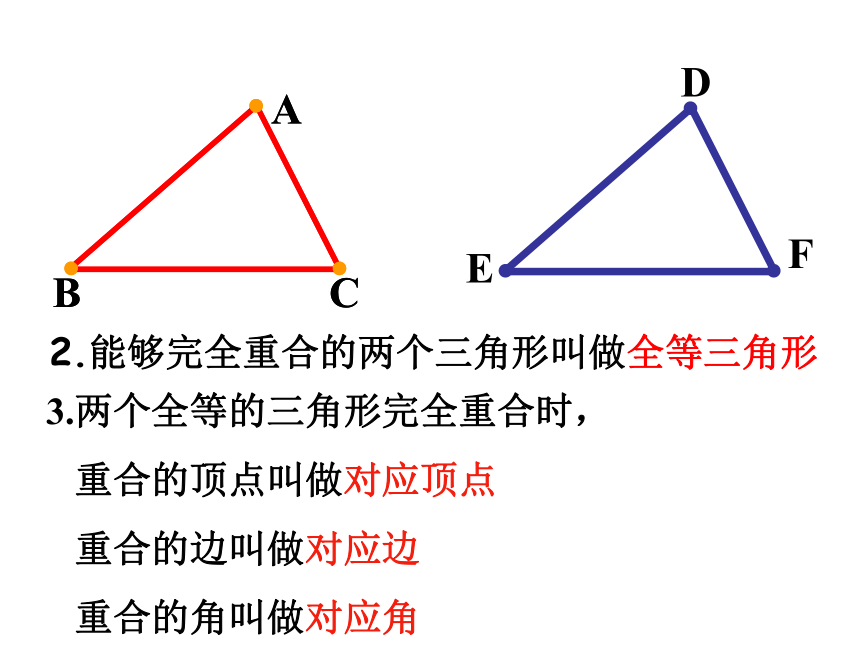
重合的顶点叫做对应顶点
重合的边叫做对应边
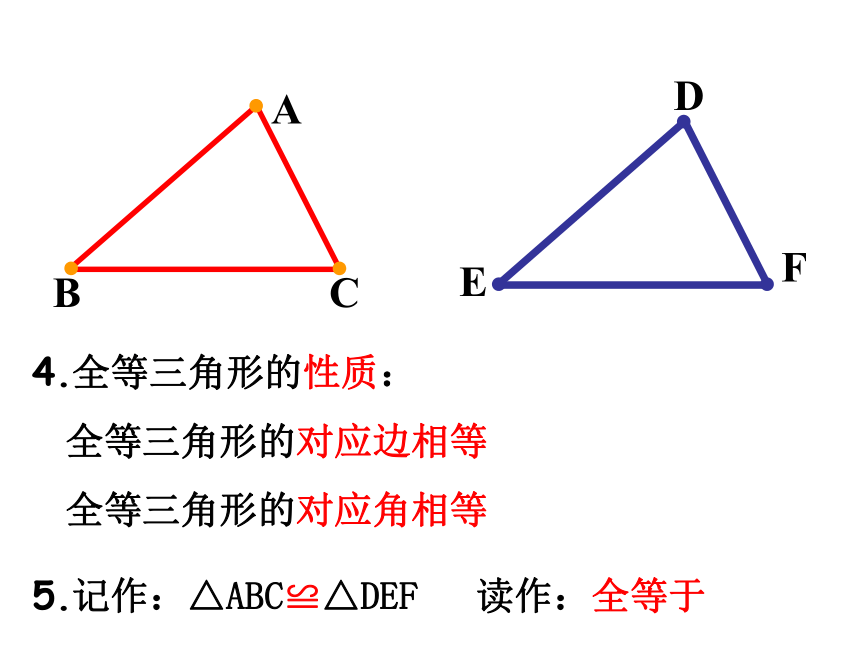
重合的角叫做对应角 2.能够完全重合的两个三角形叫做全等三角形4.全等三角形的性质:
全等三角形的对应边相等
全等三角形的对应角相等5.记作:△ABC≌△DEF 读作:全等于思考(1)其中一个三角形怎样运动得到另一三角形。
(2)找对应顶点,对应边,对应角寻找对应边对应角的规律
1.有公共边,则公共边为对应边
2.有公共角,则公共角为对应角
(对顶角为对应角)
3.最大边与最大边(最小边与最小边) 为 对应边;最大角与最大角(最小角与最小角)为对应角ABDEC例4 如图△ABC≌△EDC,∠A=∠E,用等式写出两个三角形其它的对应角和对应边。
对顶角为对应角对应角:∠B=∠D ∠ACB=∠ECD
对应边:AB=ED
AC=EC
BC=DC例2 如图:已知△ABD≌△ACE,且AB=AC,用等式写出两个三角形的其它对应边和对应角。
公共角为对应角对应边:AD=AE BD=CE
对应角:∠A=∠A
∠ADB=∠AEC
∠B=∠C例2 如图△ABC≌△CDA,AB=CD,用等式写出两个三角形其它的对应边和对应角。
对应边:AD=CB AC=CA
对应角:∠CAB=∠ACD
∠ B=∠D
∠ ACB=∠CADCBA例1 如图:△ABC≌△ABD,且AC=AD,用等式写出这两个三角形的其它对应边和对应角。 公共边为对应边对应边:BC=BD AB=AB
对应角:∠CAB=∠DAB ∠C=∠D
∠ CBA=∠DBA试一试1。如果?ABC≌ ?ADC,AB=AD, ∠B=120°,BC=3cm,那么∠D=____,DC=____cm2.如果 ?ABC≌ ?DEF,且?ABC的周长为100cm,A、B分别与D 、E对应, AB=30cm,DF=25cm,则BC的长为( )
A.45cm B.55cm
C.30cm D.25cm120°3A如图:△ABD≌△ACE ,AD=3,AC=7,求BE的长3.如图,矩形ABCD沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,DM=5cm, ∠DAM=39°,则AN=___cm, NM=___cm, ∠NAB=___.7cm5 cm)39°7512°如图,已知△ AOC ≌ △BOD
求证:AC∥BD能力提高例3 已知如图 ,△ABE≌△ACD,∠C=20o,AB=10,AD=4,G为AB延长线上的一点。
求 ∠EBG的度数及CE的长。
ECADBGF解:∵△ABE≌△ACD ∠C=20°
∴∠ABE=∠C=20°
∵AB=10 AD=4
∴AC=AB=10 AE=AD=4
∴CE=6EFABCD图5 解:∵△ACF≌△DBE
∠ E=∠F
∴AC=DB
∴AC-BC=DB-BC
即AB=DC
∵AD=9㎝,BC=5㎝
∴AB=2㎝
练习1 如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。求证:∠A=∠D。证明:∵BE=CF(已知)即 BC=EF在△ABC和△DEF中AB=DE(已知)AC=BF(已知)BC=EF(已证)∴△ABC≌△DEF(SSS)∴∠A=∠D(全等三角形对应角相等)小结:欲证角相等,转化为证三角形全等。∴ BE+EC=CF+EC
数学是思维的修炼
数学是思维的艺术
数学是智力的阶梯全等三角形同一张底片洗出的照片是
能够完全重合的(1)(2)(3)全等形:能够完全重合的两 个图形称为全等形如果把这些图形叠合起来,会怎样呢?完全重合3.两个全等的三角形完全重合时,
重合的顶点叫做对应顶点
重合的边叫做对应边
重合的角叫做对应角 2.能够完全重合的两个三角形叫做全等三角形4.全等三角形的性质:
全等三角形的对应边相等
全等三角形的对应角相等5.记作:△ABC≌△DEF 读作:全等于思考(1)其中一个三角形怎样运动得到另一三角形。
(2)找对应顶点,对应边,对应角寻找对应边对应角的规律
1.有公共边,则公共边为对应边
2.有公共角,则公共角为对应角
(对顶角为对应角)
3.最大边与最大边(最小边与最小边) 为 对应边;最大角与最大角(最小角与最小角)为对应角ABDEC例4 如图△ABC≌△EDC,∠A=∠E,用等式写出两个三角形其它的对应角和对应边。
对顶角为对应角对应角:∠B=∠D ∠ACB=∠ECD
对应边:AB=ED
AC=EC
BC=DC例2 如图:已知△ABD≌△ACE,且AB=AC,用等式写出两个三角形的其它对应边和对应角。
公共角为对应角对应边:AD=AE BD=CE
对应角:∠A=∠A
∠ADB=∠AEC
∠B=∠C例2 如图△ABC≌△CDA,AB=CD,用等式写出两个三角形其它的对应边和对应角。
对应边:AD=CB AC=CA
对应角:∠CAB=∠ACD
∠ B=∠D
∠ ACB=∠CADCBA例1 如图:△ABC≌△ABD,且AC=AD,用等式写出这两个三角形的其它对应边和对应角。 公共边为对应边对应边:BC=BD AB=AB
对应角:∠CAB=∠DAB ∠C=∠D
∠ CBA=∠DBA试一试1。如果?ABC≌ ?ADC,AB=AD, ∠B=120°,BC=3cm,那么∠D=____,DC=____cm2.如果 ?ABC≌ ?DEF,且?ABC的周长为100cm,A、B分别与D 、E对应, AB=30cm,DF=25cm,则BC的长为( )
A.45cm B.55cm
C.30cm D.25cm120°3A如图:△ABD≌△ACE ,AD=3,AC=7,求BE的长3.如图,矩形ABCD沿AM折叠,使D点落在BC上的N点处,如果AD=7cm,DM=5cm, ∠DAM=39°,则AN=___cm, NM=___cm, ∠NAB=___.7cm5 cm)39°7512°如图,已知△ AOC ≌ △BOD
求证:AC∥BD能力提高例3 已知如图 ,△ABE≌△ACD,∠C=20o,AB=10,AD=4,G为AB延长线上的一点。
求 ∠EBG的度数及CE的长。
ECADBGF解:∵△ABE≌△ACD ∠C=20°
∴∠ABE=∠C=20°
∵AB=10 AD=4
∴AC=AB=10 AE=AD=4
∴CE=6EFABCD图5 解:∵△ACF≌△DBE
∠ E=∠F
∴AC=DB
∴AC-BC=DB-BC
即AB=DC
∵AD=9㎝,BC=5㎝
∴AB=2㎝
练习1 如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。求证:∠A=∠D。证明:∵BE=CF(已知)即 BC=EF在△ABC和△DEF中AB=DE(已知)AC=BF(已知)BC=EF(已证)∴△ABC≌△DEF(SSS)∴∠A=∠D(全等三角形对应角相等)小结:欲证角相等,转化为证三角形全等。∴ BE+EC=CF+EC
