苏南中学2013-2014学年度沪科版八年级数学上册第三次月考试卷(附答案解析)
文档属性
| 名称 | 苏南中学2013-2014学年度沪科版八年级数学上册第三次月考试卷(附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 161.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-12 10:56:27 | ||
图片预览

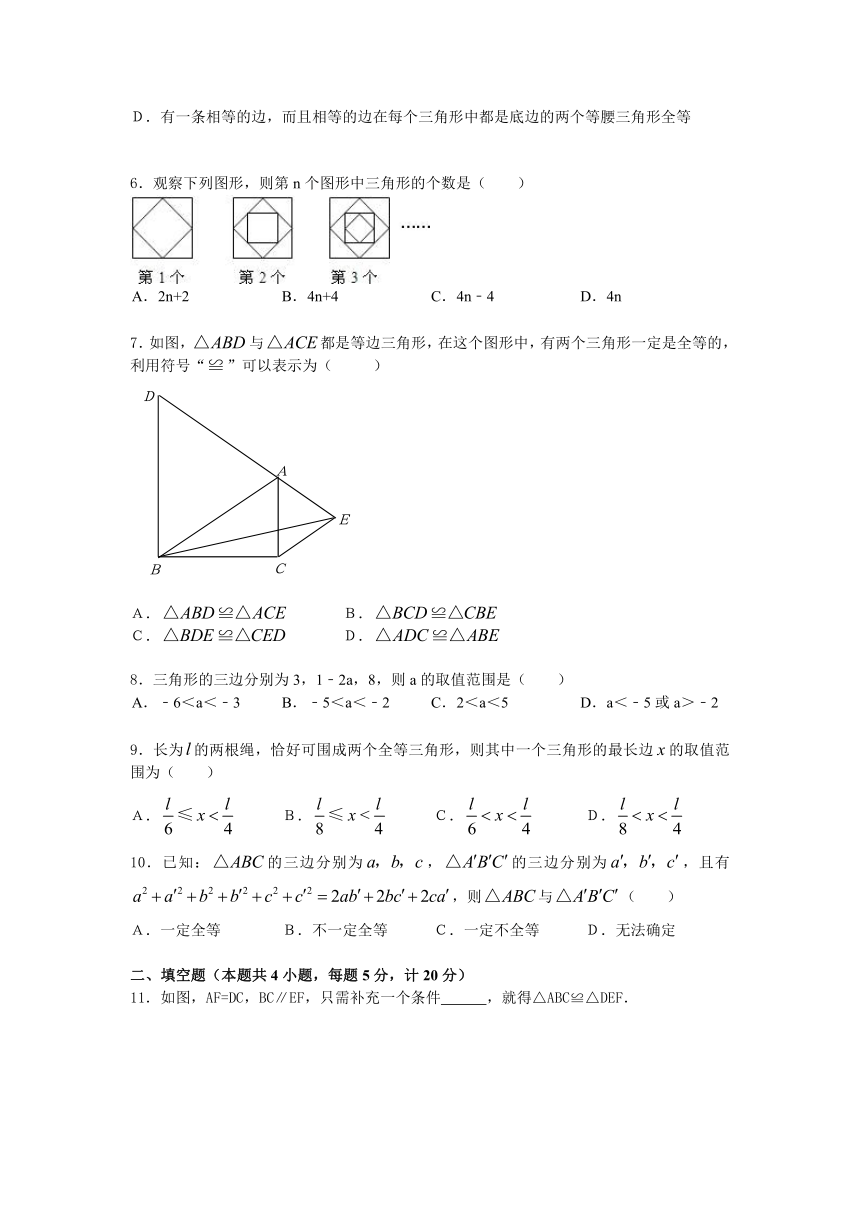
文档简介
苏南中学2013-2014学年度沪科版八年级(上)
数学月考试卷
(考试范围:第14章《全等三角形》;考试时间:120分钟;满分150分)
一、选择题(本题共10小题,每题4分,计40分)
1.如图,已知a∥b,∠1=105°,∠2=140°,则∠3=( )
A. 55° B. 60° C. 65° D. 70°
2.如图,中,,,则由“”可以判定( )
A. B.
C. D.以上答案都不对
3.如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以( )
A.带①去 B.带②去 C.带③去 D.带①和②去
4.如果是中边上一点,并且,则是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
5.下列说法正确的是( )
A.若,且的两条直角边分别是水平和竖直状态,那么的两条直角边也一定分别是水平和竖直状态
B.如果,,那么
C.有一条公共边,而且公共边在每个三角形中都是腰的两个等腰三角形一定全等
D.有一条相等的边,而且相等的边在每个三角形中都是底边的两个等腰三角形全等
6.观察下列图形,则第n个图形中三角形的个数是( )
A. 2n+2 B. 4n+4 C. 4n﹣4 D. 4n
7.如图,与都是等边三角形,在这个图形中,有两个三角形一定是全等的,利用符号“”可以表示为( )
A. B.
C. D.
8.三角形的三边分别为3,1﹣2a,8,则a的取值范围是( )
A. ﹣6<a<﹣3 B. ﹣5<a<﹣2 C. 2<a<5 D. a<﹣5或a>﹣2
9.长为的两根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边的取值范围为( )
A. B. C. D.
10.已知:的三边分别为,的三边分别为,且有,则与( )
A.一定全等 B.不一定全等 C.一定不全等 D.无法确定
二、填空题(本题共4小题,每题5分,计20分)
11.如图,AF=DC,BC∥EF,只需补充一个条件 ,就得△ABC≌△DEF.
12.如图,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ= °.
13.如图,已知△ABC≌△CDA,∠BAC=60°,∠DAC=23°,则∠D= .
14.两组邻边分别相等的四边形我们称它为筝形.如图,在四边形中,,,与相交于点,下列判断正确的有 .(填序号).
①;
②、互相平分;
③平分;
④;
⑤筝形的面积为.
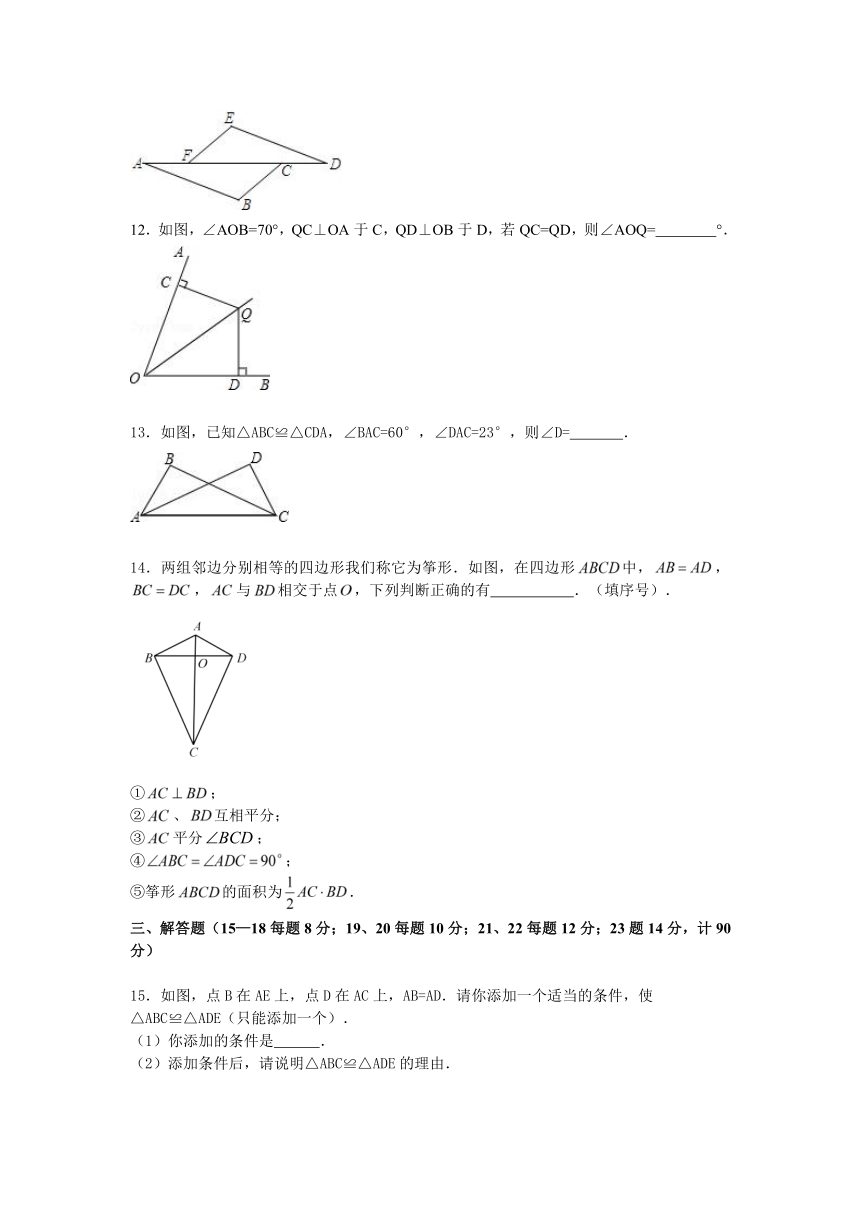
三、解答题(15—18每题8分;19、20每题10分;21、22每题12分;23题14分,计90分)
15.如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使
△ABC≌△ADE(只能添加一个).
(1)你添加的条件是 .
(2)添加条件后,请说明△ABC≌△ADE的理由.
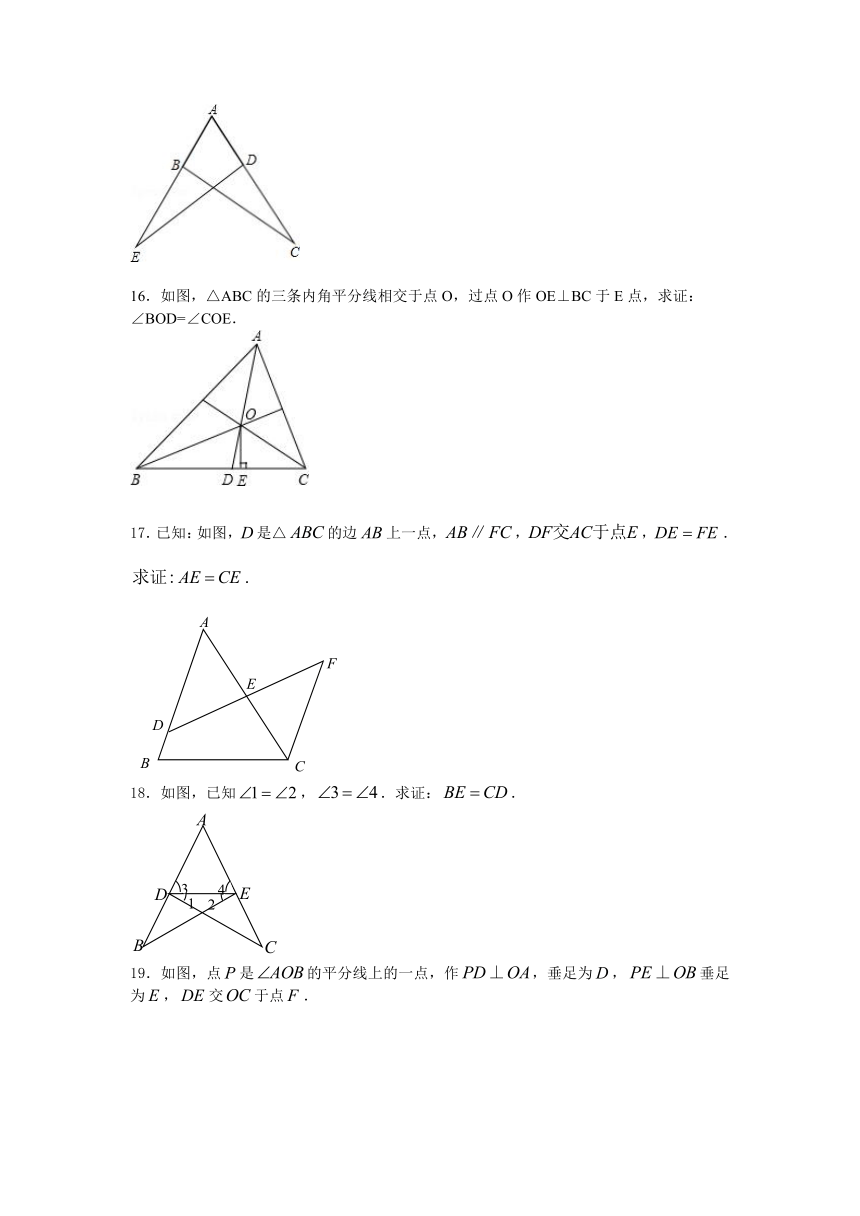
16.如图,△ABC的三条内角平分线相交于点O,过点O作OE⊥BC于E点,求证:∠BOD=∠COE.
17.已知:如图,是△的边上一点,,,.
.
18.如图,已知,.求证:.
19.如图,点是的平分线上的一点,作,垂足为,垂足为,交于点.
(1)你能找到几对全等三角形?请说明理由;
(2)你能确定图中共有几个直角吗?请说明理由.
20.如图,已知为等边三角形,,垂足为,,垂足为,,垂足为,且
求证:为等边三角形.
21.如图所示,,,,,,,求:
(1)的度数;
(2)的长.
22.如图,,且,,,求和的度数.
23.你能沿虚线把下面图形划分成两个全等图形吗?请找出三种方法.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D B D D B A A
11.BC=EF(答案不唯一)
12.35
13.97°
14.①、③、⑤
15.解:(1)∠C=∠E。
(2)选∠C=∠E为条件,理由如下:
在△ABC和△ADE中,∠A=∠A,∠C=∠E,AB=AD,∴△ABC≌△ADE(AAS)。
16. 证明:∵∠AFO=∠FBC+∠ACB=∠ABC+∠ACB,∴∠AOF=180°﹣(∠DAC+∠AF0)=180°﹣[∠BAC+∠ABC+∠ACB]=180°﹣[(∠BAC+∠ABC)+∠ACB]=180°﹣[(180°﹣∠ACB)+∠ACB]=180°﹣[90°+∠ACB]=90°﹣∠ACB,∴∠BOD=∠AOF=90°﹣∠ACB,又∵在直角△OCE中,∠COE=90°﹣∠OCD=90°﹣∠ACB,∴∠BOD=∠COE.
17.略
18.略
19.(1)有三对全等三角形;(2)共有八个直角.
20.略
21.(1) (2)
22.
23.如图所示:
①
②
③
E
A
C
B
D
A
D
B
C
F
E
1
2
3
4
1
(1)
(2)
(2)
(1)
数学月考试卷
(考试范围:第14章《全等三角形》;考试时间:120分钟;满分150分)
一、选择题(本题共10小题,每题4分,计40分)
1.如图,已知a∥b,∠1=105°,∠2=140°,则∠3=( )
A. 55° B. 60° C. 65° D. 70°
2.如图,中,,,则由“”可以判定( )
A. B.
C. D.以上答案都不对
3.如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以( )
A.带①去 B.带②去 C.带③去 D.带①和②去
4.如果是中边上一点,并且,则是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形
5.下列说法正确的是( )
A.若,且的两条直角边分别是水平和竖直状态,那么的两条直角边也一定分别是水平和竖直状态
B.如果,,那么
C.有一条公共边,而且公共边在每个三角形中都是腰的两个等腰三角形一定全等
D.有一条相等的边,而且相等的边在每个三角形中都是底边的两个等腰三角形全等
6.观察下列图形,则第n个图形中三角形的个数是( )
A. 2n+2 B. 4n+4 C. 4n﹣4 D. 4n
7.如图,与都是等边三角形,在这个图形中,有两个三角形一定是全等的,利用符号“”可以表示为( )
A. B.
C. D.
8.三角形的三边分别为3,1﹣2a,8,则a的取值范围是( )
A. ﹣6<a<﹣3 B. ﹣5<a<﹣2 C. 2<a<5 D. a<﹣5或a>﹣2
9.长为的两根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边的取值范围为( )
A. B. C. D.
10.已知:的三边分别为,的三边分别为,且有,则与( )
A.一定全等 B.不一定全等 C.一定不全等 D.无法确定
二、填空题(本题共4小题,每题5分,计20分)
11.如图,AF=DC,BC∥EF,只需补充一个条件 ,就得△ABC≌△DEF.
12.如图,∠AOB=70°,QC⊥OA于C,QD⊥OB于D,若QC=QD,则∠AOQ= °.
13.如图,已知△ABC≌△CDA,∠BAC=60°,∠DAC=23°,则∠D= .
14.两组邻边分别相等的四边形我们称它为筝形.如图,在四边形中,,,与相交于点,下列判断正确的有 .(填序号).
①;
②、互相平分;
③平分;
④;
⑤筝形的面积为.
三、解答题(15—18每题8分;19、20每题10分;21、22每题12分;23题14分,计90分)
15.如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使
△ABC≌△ADE(只能添加一个).
(1)你添加的条件是 .
(2)添加条件后,请说明△ABC≌△ADE的理由.
16.如图,△ABC的三条内角平分线相交于点O,过点O作OE⊥BC于E点,求证:∠BOD=∠COE.
17.已知:如图,是△的边上一点,,,.
.
18.如图,已知,.求证:.
19.如图,点是的平分线上的一点,作,垂足为,垂足为,交于点.
(1)你能找到几对全等三角形?请说明理由;
(2)你能确定图中共有几个直角吗?请说明理由.
20.如图,已知为等边三角形,,垂足为,,垂足为,,垂足为,且
求证:为等边三角形.
21.如图所示,,,,,,,求:
(1)的度数;
(2)的长.
22.如图,,且,,,求和的度数.
23.你能沿虚线把下面图形划分成两个全等图形吗?请找出三种方法.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C D B D D B A A
11.BC=EF(答案不唯一)
12.35
13.97°
14.①、③、⑤
15.解:(1)∠C=∠E。
(2)选∠C=∠E为条件,理由如下:
在△ABC和△ADE中,∠A=∠A,∠C=∠E,AB=AD,∴△ABC≌△ADE(AAS)。
16. 证明:∵∠AFO=∠FBC+∠ACB=∠ABC+∠ACB,∴∠AOF=180°﹣(∠DAC+∠AF0)=180°﹣[∠BAC+∠ABC+∠ACB]=180°﹣[(∠BAC+∠ABC)+∠ACB]=180°﹣[(180°﹣∠ACB)+∠ACB]=180°﹣[90°+∠ACB]=90°﹣∠ACB,∴∠BOD=∠AOF=90°﹣∠ACB,又∵在直角△OCE中,∠COE=90°﹣∠OCD=90°﹣∠ACB,∴∠BOD=∠COE.
17.略
18.略
19.(1)有三对全等三角形;(2)共有八个直角.
20.略
21.(1) (2)
22.
23.如图所示:
①
②
③
E
A
C
B
D
A
D
B
C
F
E
1
2
3
4
1
(1)
(2)
(2)
(1)
