人教版六年级数学上册《圆的面积公式及应用》教学课件(共26张PPT)
文档属性
| 名称 | 人教版六年级数学上册《圆的面积公式及应用》教学课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 15:29:27 | ||
图片预览




文档简介
(共26张PPT)
圆的面积公式及应用
第五单元 圆
输入标题
学习目标
培养动手操作、抽象概括的能力,在推导公式的过程中渗透转化的数学思想,初步了解极限思想。
通过观察、操作、分析和讨论推导圆面积的计算公式,掌握圆面积的计算公式,并能解决一些简单的实际问题。
准备好了吗?一起去探索吧!
圆的面积
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
仔细观察下面的2幅图,想一想它们有什么相似之处?
(1)
(2)
平行四边形面积=底×高
长方形面积=长×宽
三角形面积=底×高÷2
平行四边形面积=底×高
它们都是将新图形转化成已学过的图形来推导面积的计算公式。
用转化的方法,我们还研究过哪些图形的面积?
复习旧知,回忆“转化”
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
复习旧知,回忆“转化”
我们利用转化的方法,将梯形转化成平行四边形或三角形来推导它的面积计算公式。
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
复习旧知,回忆“转化”
也可以利用转化的方法,把圆转化成学过的长方形、平行四边形、三角形或梯形来研究。
怎么研究圆的面积?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
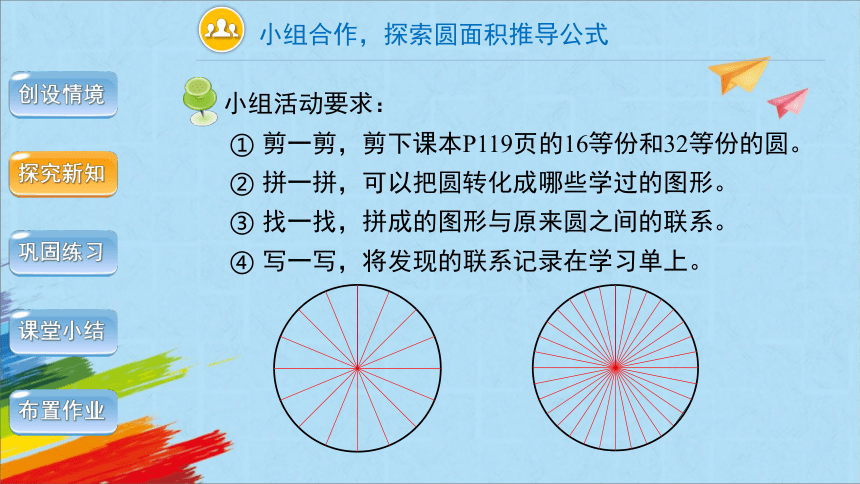
小组合作,探索圆面积推导公式
小组活动要求:
① 剪一剪,剪下课本P119页的16等份和32等份的圆。
② 拼一拼,可以把圆转化成哪些学过的图形。
③ 找一找,拼成的图形与原来圆之间的联系。
④ 写一写,将发现的联系记录在学习单上。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
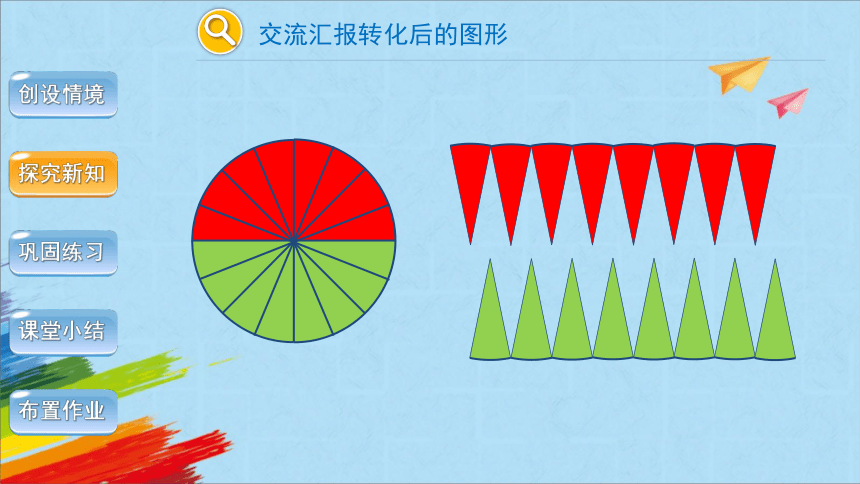
交流汇报转化后的图形
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
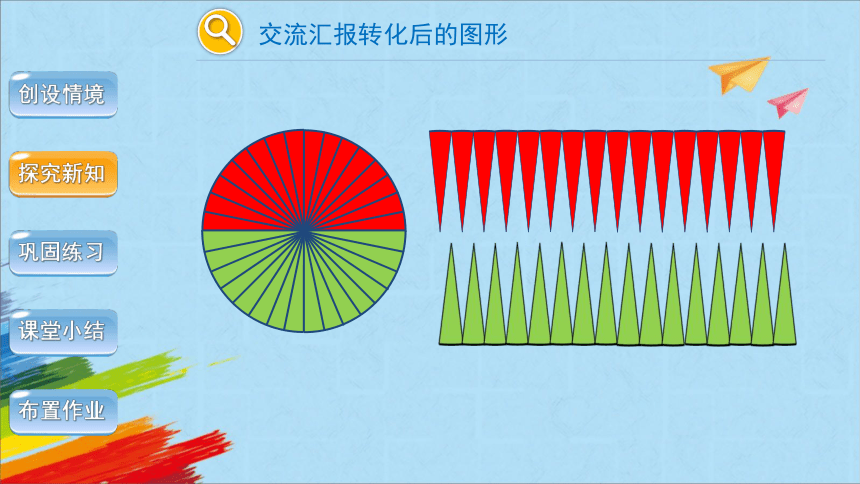
交流汇报转化后的图形
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
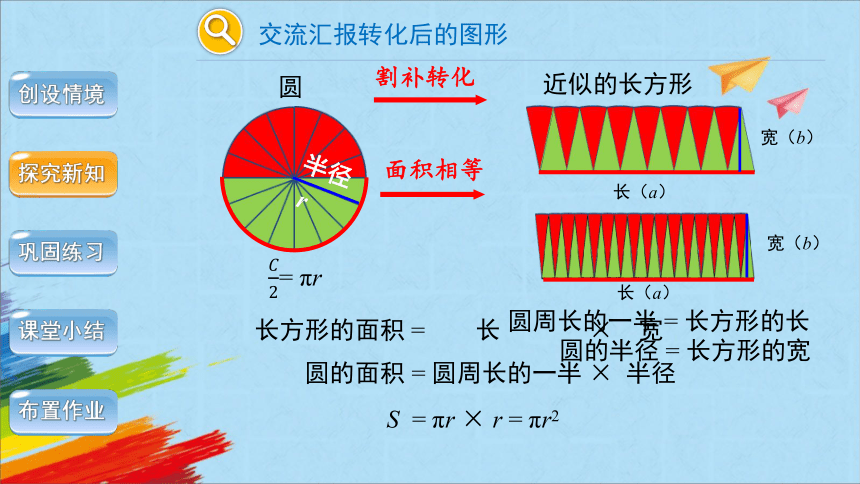
交流汇报转化后的图形
圆
近似的长方形
圆的半径 = 长方形的宽
割补转化
面积相等
长(a)
半径
r
宽(b)
宽(b)
圆周长的一半 = 长方形的长
长方形的面积 = 长 × 宽
圆的面积 = 圆周长的一半 × 半径
长(a)
S = πr × r = πr2
= πr
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报,推导圆面积计算公式
三角形
梯形
圆
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报,推导圆面积计算公式
三角形
圆
圆的半径是r,三角形的底近似于( ),高近似于( ) 。
因为三角形的面积=( ),
所以圆的面积:S=( )=( )。
4r
底×高÷2
πr2
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报,推导圆面积计算公式
梯形
圆
圆的半径是r,梯形的上底近似于( ),下底近似于( ),高近似于( )。
因为梯形的面积=( ),
所以圆的面积:S=( )=( )。
(上底+下底)×高÷2
πr2
2r
()×2r÷2
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
总结圆面积计算公式
将圆分成若干等份,可以把圆转化成长方形、三角形、梯形,依据转化的图形,可以推导出圆的面积计算公式:
S=πr2
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
怎么解决这个问题?
先计算出圆的半径,根据圆的半径求出圆形草坪的面积,最后用草坪的面积乘草皮的单价求出总价。
圆形草坪的直径为20 m,每平方米草皮8元。铺满草皮需要多少钱?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
圆形草坪的直径为20 m,每平方米草皮8元。铺满草皮需要多少钱?
圆形草坪的半径
20÷2=10(m)
3.14×10 =314(m )
314×8=2512(元)
圆形草坪的面积
草皮的总价
答:铺满草皮需要2512元。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
圆环指的是什么?它的面积怎么算?
大圆里挖去了一个小的同心圆,剩余的部分就是圆环。它的面积可以用大圆的面积减去小圆的面积来计算。
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
可以这样算:
3.14×62-3.14×22
=3.14×36-3.14×4
=100.48(cm2)
还可以这样算:
3.14×(62-22)
=3.14×(36-4)
=100.48(cm2)
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
答:圆环的面积是100.48 cm 。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
圆环的面积这样算可以吗?
不可以,因为圆环不是圆,不能用圆面积公式来计算。
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
3.14×(6-2)2
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
1.一个圆形茶几桌面的直径是1 m,它的面积是多少平方米?
1÷2=0.5(m)
3.14×0.5 =0.785(m )
答:茶几桌面的面积是0.785 m 。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
2.一个圆形环岛的直径是50 m,中间是一个直径为10 m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
50÷2=25(m) 10÷2=5(m)
3.14×(25 -5 )
=3.14×600
=1884(m )
答:草坪的占地面积是1884平方米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
(1)一个圆的面积是3米。( )
×
“米”是长度单位,不是面积单位。
3. 判断对错,并说明理由。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
(2)半径是2厘米的圆,周长和面积相等。( )
×
周长和面积是两个不同的概念,无法比较。
3. 判断对错,并说明理由。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
3. 判断对错,并说明理由。
(3)圆的半径扩大5倍,圆的面积也扩大5倍。( )
×
半径扩大5倍,面积应该扩大25倍。
输入标题
布置作业
创设情境
巩固练习
课堂小结
探究新知
方法:圆割补转化成其他图形
联系:面积不变
结论:S=πr2
你有什么收获?
输入标题
创设情境
巩固练习
课堂小结
布置作业
探究新知
教材P71第3题、第4题;教材P72第5题、第6题。
再见
圆的面积公式及应用
第五单元 圆
输入标题
学习目标
培养动手操作、抽象概括的能力,在推导公式的过程中渗透转化的数学思想,初步了解极限思想。
通过观察、操作、分析和讨论推导圆面积的计算公式,掌握圆面积的计算公式,并能解决一些简单的实际问题。
准备好了吗?一起去探索吧!
圆的面积
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
仔细观察下面的2幅图,想一想它们有什么相似之处?
(1)
(2)
平行四边形面积=底×高
长方形面积=长×宽
三角形面积=底×高÷2
平行四边形面积=底×高
它们都是将新图形转化成已学过的图形来推导面积的计算公式。
用转化的方法,我们还研究过哪些图形的面积?
复习旧知,回忆“转化”
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
复习旧知,回忆“转化”
我们利用转化的方法,将梯形转化成平行四边形或三角形来推导它的面积计算公式。
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
复习旧知,回忆“转化”
也可以利用转化的方法,把圆转化成学过的长方形、平行四边形、三角形或梯形来研究。
怎么研究圆的面积?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
小组合作,探索圆面积推导公式
小组活动要求:
① 剪一剪,剪下课本P119页的16等份和32等份的圆。
② 拼一拼,可以把圆转化成哪些学过的图形。
③ 找一找,拼成的图形与原来圆之间的联系。
④ 写一写,将发现的联系记录在学习单上。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报转化后的图形
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报转化后的图形
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报转化后的图形
圆
近似的长方形
圆的半径 = 长方形的宽
割补转化
面积相等
长(a)
半径
r
宽(b)
宽(b)
圆周长的一半 = 长方形的长
长方形的面积 = 长 × 宽
圆的面积 = 圆周长的一半 × 半径
长(a)
S = πr × r = πr2
= πr
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报,推导圆面积计算公式
三角形
梯形
圆
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报,推导圆面积计算公式
三角形
圆
圆的半径是r,三角形的底近似于( ),高近似于( ) 。
因为三角形的面积=( ),
所以圆的面积:S=( )=( )。
4r
底×高÷2
πr2
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
交流汇报,推导圆面积计算公式
梯形
圆
圆的半径是r,梯形的上底近似于( ),下底近似于( ),高近似于( )。
因为梯形的面积=( ),
所以圆的面积:S=( )=( )。
(上底+下底)×高÷2
πr2
2r
()×2r÷2
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
总结圆面积计算公式
将圆分成若干等份,可以把圆转化成长方形、三角形、梯形,依据转化的图形,可以推导出圆的面积计算公式:
S=πr2
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
怎么解决这个问题?
先计算出圆的半径,根据圆的半径求出圆形草坪的面积,最后用草坪的面积乘草皮的单价求出总价。
圆形草坪的直径为20 m,每平方米草皮8元。铺满草皮需要多少钱?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
圆形草坪的直径为20 m,每平方米草皮8元。铺满草皮需要多少钱?
圆形草坪的半径
20÷2=10(m)
3.14×10 =314(m )
314×8=2512(元)
圆形草坪的面积
草皮的总价
答:铺满草皮需要2512元。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
圆环指的是什么?它的面积怎么算?
大圆里挖去了一个小的同心圆,剩余的部分就是圆环。它的面积可以用大圆的面积减去小圆的面积来计算。
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
可以这样算:
3.14×62-3.14×22
=3.14×36-3.14×4
=100.48(cm2)
还可以这样算:
3.14×(62-22)
=3.14×(36-4)
=100.48(cm2)
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
答:圆环的面积是100.48 cm 。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
圆面积计算公式的应用
圆环的面积这样算可以吗?
不可以,因为圆环不是圆,不能用圆面积公式来计算。
光盘的银色部分是一个圆环,内圆半径是2 cm,外圆半径是6 cm。圆环的面积是多少?
3.14×(6-2)2
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
1.一个圆形茶几桌面的直径是1 m,它的面积是多少平方米?
1÷2=0.5(m)
3.14×0.5 =0.785(m )
答:茶几桌面的面积是0.785 m 。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
2.一个圆形环岛的直径是50 m,中间是一个直径为10 m的圆形花坛,其他地方是草坪。草坪的占地面积是多少?
50÷2=25(m) 10÷2=5(m)
3.14×(25 -5 )
=3.14×600
=1884(m )
答:草坪的占地面积是1884平方米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
(1)一个圆的面积是3米。( )
×
“米”是长度单位,不是面积单位。
3. 判断对错,并说明理由。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
(2)半径是2厘米的圆,周长和面积相等。( )
×
周长和面积是两个不同的概念,无法比较。
3. 判断对错,并说明理由。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
3. 判断对错,并说明理由。
(3)圆的半径扩大5倍,圆的面积也扩大5倍。( )
×
半径扩大5倍,面积应该扩大25倍。
输入标题
布置作业
创设情境
巩固练习
课堂小结
探究新知
方法:圆割补转化成其他图形
联系:面积不变
结论:S=πr2
你有什么收获?
输入标题
创设情境
巩固练习
课堂小结
布置作业
探究新知
教材P71第3题、第4题;教材P72第5题、第6题。
再见
