人教版 六年级数学上册 第五单元《解决问题》课件 (共23张PPT)
文档属性
| 名称 | 人教版 六年级数学上册 第五单元《解决问题》课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 15:33:39 | ||
图片预览






文档简介
(共23张PPT)
解决问题
第五单元 圆
5 × =1
1
5
0.25 × 4 =1
× =1
2
3
3
2
输入标题
学习目标
经历尝试、探究、分析、反思等过程,在解决一些与外方内圆、外圆内方有关的数学问题的过程中,发展推理能力,提高问题解决的能力,渗透转化和模型的数学思想。
结合具体情境认识与圆相关的组合图形的特征,掌握计算此类图形面积的方法,并能准确计算。
准备好了吗?一起去探索吧!
解决问题
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
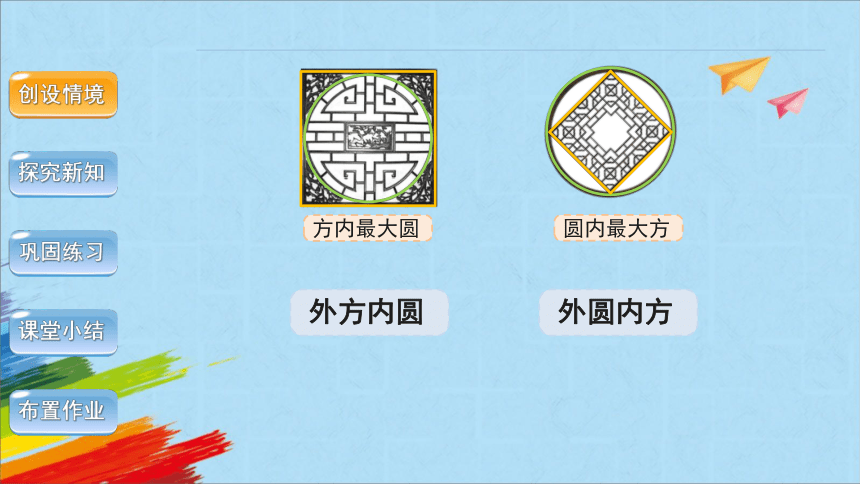
欣赏苏州园林门窗的图案设计。
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
这两个图案设计有什么特点?
探究新知
创设情境
巩固练习
课堂小结
布置作业
下面两个图案中也有正方形、有圆,和上面的有什么不同?
方内最大圆
圆内最大方
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
外方内圆
外圆内方
方内最大圆
圆内最大方
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
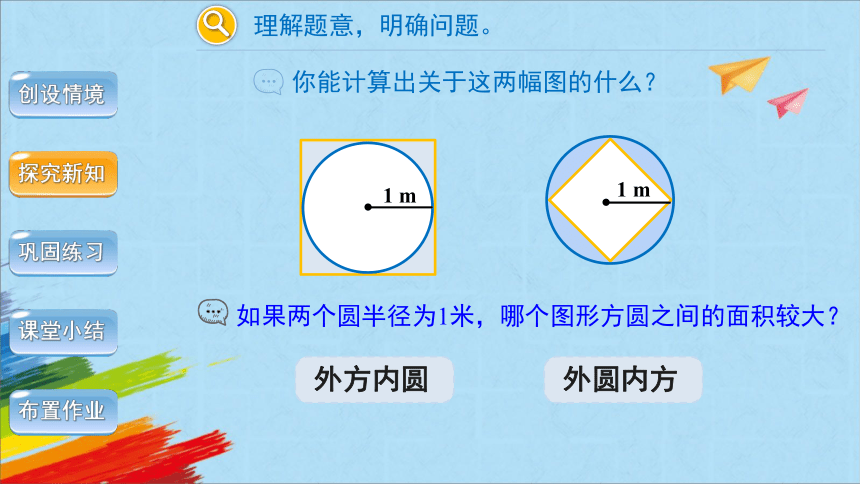
理解题意,明确问题。
你能计算出关于这两幅图的什么?
外方内圆
1 m
1 m
如果两个圆半径为1米,哪个图形方圆之间的面积较大?
外圆内方
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
外方内圆
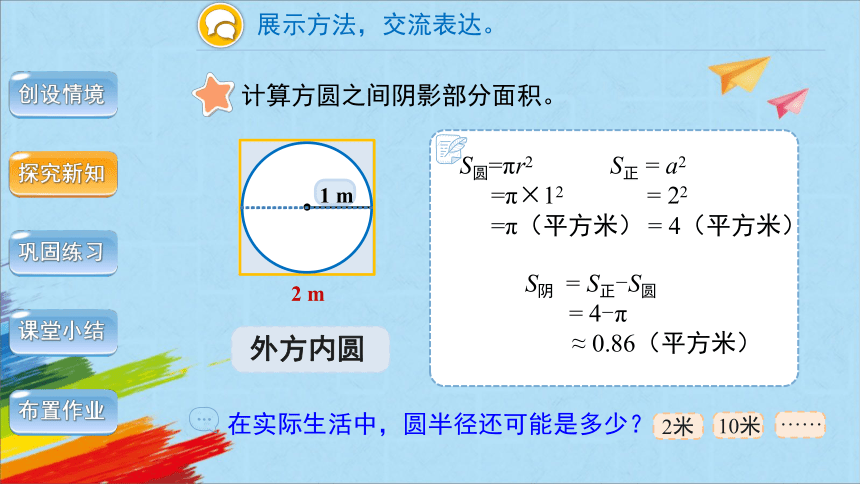
展示方法,交流表达。
计算方圆之间阴影部分面积。
2 m
S圆=πr2
=π×12
=π(平方米)
1 m
S正 = a2
= 22
= 4(平方米)
S阴 = S正-S圆
= 4-π
≈ 0.86(平方米)
在实际生活中,圆半径还可能是多少?
2米
10米
……
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
展示方法,交流表达。
计算方圆之间阴影部分面积。
外方内圆
选择任意一个数作为半径的值
在实际生活中,圆半径还可能是多少?
2米
10米
……
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
展示方法,交流表达。
计算方圆之间阴影部分面积。
1 m
10 m
2 m
半径取值不同,结果也不同,有什么好方法,能够表示出半径所有的情况?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
展示方法,交流表达。
计算方圆之间阴影部分面积。
r
S阴=S正-S圆
= (2r)2-πr2
=4r2-πr2
= (4-π)r2
≈ 0.86r2
当r=1时,
0.86r2=0.86
当r=2时,
0.86r2=3.44
当r=10时,0.86r2=86
将刚才3个半径的数据代入计算一下吧!
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
外圆内方
展示方法,交流表达。
计算方圆之间阴影部分面积。
S圆=πr2
r
S三角形=2r×r÷2=r2
正方形边长不知道,怎么求面积?
r
r
S正=r2 ×2=2r2
S阴=S圆-S正
=πr2-2r2
≈1.14r2
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
r
r
S阴=S圆-S正
=πr2-2r2
≈1.14r2
S阴=S正-S圆
= (4-π)r2
≈ 0.86r2
如果两个圆半径为r米,哪个图形方圆之间的面积较大?
<
展示方法,交流表达。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
下面两幅图中,两个圆完全相同,如果半径用字母r表示,你能写出外面正方形、圆、里面正方形的面积比吗?
提升拓展,发展思维。
r
r
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
提升拓展,发展思维。
r
r
S圆 = πr2
S外方=4r2
S内方= 2r2
S外方 : S圆 : S内方 = 4 : π : 2
下面两幅图中,两个圆完全相同,如果半径用字母r表示,你能写出外面正方形、圆、里面正方形的面积比吗?
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
1.解决实际问题。
公园的正方形草地上,一个自动放置喷灌装置的射程是5米,这块草地中不能被自动浇灌的面积是多少?
5 m
5 m
S圆=πr2
= π×52
= 25π(m2)
S正= a2
= 102
= 100(m2)
S阴= S正-S圆
= 100-25π
≈ 21.5(m2)
方法 一
答:这块草地中不能被自动浇灌的面积是21.5平方米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
1.解决实际问题。
公园的正方形草地上,一个自动放置喷灌装置的射程是5米,这块草地中不能被自动浇灌的面积是多少?
5 m
5 m
S阴=0.86r2
= 0.86×52
= 0.86×25
= 21.5(m2)
方法 二
答:这块草地中不能被自动浇灌的面积是21.5平方米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
2.解决实际问题。
在一块面积是300平方米的正方形草地上,建一个最大的圆形花坛,如何建?你能求出花坛的占地面积吗?
边长求不出,怎么办?
S外方 : S圆=4 : π
300÷4×π≈235.5(m2)
答:花坛的占地面积是235.5平方米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
3.计算图形面积。
如图,如果正方形的面积是8 cm2,在正方形里画一个最大的扇形,那么阴影部分的面积是多少平方厘米?
边长求不出,怎么办?
S阴=0.86×8÷4=1.72(cm2)
答:阴影部分的面积是1.72平方厘米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
你还能像这样在正方形内画一个图形,使正方形面积和所画图形的面积比是4∶π吗?
输入标题
布置作业
创设情境
巩固练习
课堂小结
探究新知
你有什么收获?
r
外方内圆
S阴=S正-S圆
=(2r)2-πr2
≈0.86r2
r
S阴=S圆-S正
=πr2-2r2
≈1.14r2
外圆内方
r
r
S外方:S圆:S内方
=4 : π : 2
输入标题
创设情境
巩固练习
课堂小结
布置作业
探究新知
教材P70 做一做。
再见
5 × =1
1
5
0.25 × 4 =1
× =1
2
3
3
2
解决问题
第五单元 圆
5 × =1
1
5
0.25 × 4 =1
× =1
2
3
3
2
输入标题
学习目标
经历尝试、探究、分析、反思等过程,在解决一些与外方内圆、外圆内方有关的数学问题的过程中,发展推理能力,提高问题解决的能力,渗透转化和模型的数学思想。
结合具体情境认识与圆相关的组合图形的特征,掌握计算此类图形面积的方法,并能准确计算。
准备好了吗?一起去探索吧!
解决问题
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
欣赏苏州园林门窗的图案设计。
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
这两个图案设计有什么特点?
探究新知
创设情境
巩固练习
课堂小结
布置作业
下面两个图案中也有正方形、有圆,和上面的有什么不同?
方内最大圆
圆内最大方
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
外方内圆
外圆内方
方内最大圆
圆内最大方
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
理解题意,明确问题。
你能计算出关于这两幅图的什么?
外方内圆
1 m
1 m
如果两个圆半径为1米,哪个图形方圆之间的面积较大?
外圆内方
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
外方内圆
展示方法,交流表达。
计算方圆之间阴影部分面积。
2 m
S圆=πr2
=π×12
=π(平方米)
1 m
S正 = a2
= 22
= 4(平方米)
S阴 = S正-S圆
= 4-π
≈ 0.86(平方米)
在实际生活中,圆半径还可能是多少?
2米
10米
……
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
展示方法,交流表达。
计算方圆之间阴影部分面积。
外方内圆
选择任意一个数作为半径的值
在实际生活中,圆半径还可能是多少?
2米
10米
……
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
展示方法,交流表达。
计算方圆之间阴影部分面积。
1 m
10 m
2 m
半径取值不同,结果也不同,有什么好方法,能够表示出半径所有的情况?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
展示方法,交流表达。
计算方圆之间阴影部分面积。
r
S阴=S正-S圆
= (2r)2-πr2
=4r2-πr2
= (4-π)r2
≈ 0.86r2
当r=1时,
0.86r2=0.86
当r=2时,
0.86r2=3.44
当r=10时,0.86r2=86
将刚才3个半径的数据代入计算一下吧!
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
外圆内方
展示方法,交流表达。
计算方圆之间阴影部分面积。
S圆=πr2
r
S三角形=2r×r÷2=r2
正方形边长不知道,怎么求面积?
r
r
S正=r2 ×2=2r2
S阴=S圆-S正
=πr2-2r2
≈1.14r2
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
r
r
S阴=S圆-S正
=πr2-2r2
≈1.14r2
S阴=S正-S圆
= (4-π)r2
≈ 0.86r2
如果两个圆半径为r米,哪个图形方圆之间的面积较大?
<
展示方法,交流表达。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
下面两幅图中,两个圆完全相同,如果半径用字母r表示,你能写出外面正方形、圆、里面正方形的面积比吗?
提升拓展,发展思维。
r
r
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
提升拓展,发展思维。
r
r
S圆 = πr2
S外方=4r2
S内方= 2r2
S外方 : S圆 : S内方 = 4 : π : 2
下面两幅图中,两个圆完全相同,如果半径用字母r表示,你能写出外面正方形、圆、里面正方形的面积比吗?
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
1.解决实际问题。
公园的正方形草地上,一个自动放置喷灌装置的射程是5米,这块草地中不能被自动浇灌的面积是多少?
5 m
5 m
S圆=πr2
= π×52
= 25π(m2)
S正= a2
= 102
= 100(m2)
S阴= S正-S圆
= 100-25π
≈ 21.5(m2)
方法 一
答:这块草地中不能被自动浇灌的面积是21.5平方米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
1.解决实际问题。
公园的正方形草地上,一个自动放置喷灌装置的射程是5米,这块草地中不能被自动浇灌的面积是多少?
5 m
5 m
S阴=0.86r2
= 0.86×52
= 0.86×25
= 21.5(m2)
方法 二
答:这块草地中不能被自动浇灌的面积是21.5平方米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
2.解决实际问题。
在一块面积是300平方米的正方形草地上,建一个最大的圆形花坛,如何建?你能求出花坛的占地面积吗?
边长求不出,怎么办?
S外方 : S圆=4 : π
300÷4×π≈235.5(m2)
答:花坛的占地面积是235.5平方米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
3.计算图形面积。
如图,如果正方形的面积是8 cm2,在正方形里画一个最大的扇形,那么阴影部分的面积是多少平方厘米?
边长求不出,怎么办?
S阴=0.86×8÷4=1.72(cm2)
答:阴影部分的面积是1.72平方厘米。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
你还能像这样在正方形内画一个图形,使正方形面积和所画图形的面积比是4∶π吗?
输入标题
布置作业
创设情境
巩固练习
课堂小结
探究新知
你有什么收获?
r
外方内圆
S阴=S正-S圆
=(2r)2-πr2
≈0.86r2
r
S阴=S圆-S正
=πr2-2r2
≈1.14r2
外圆内方
r
r
S外方:S圆:S内方
=4 : π : 2
输入标题
创设情境
巩固练习
课堂小结
布置作业
探究新知
教材P70 做一做。
再见
5 × =1
1
5
0.25 × 4 =1
× =1
2
3
3
2
