全等三角形的复习课[上学期]
文档属性
| 名称 | 全等三角形的复习课[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-21 00:00:00 | ||
图片预览






文档简介
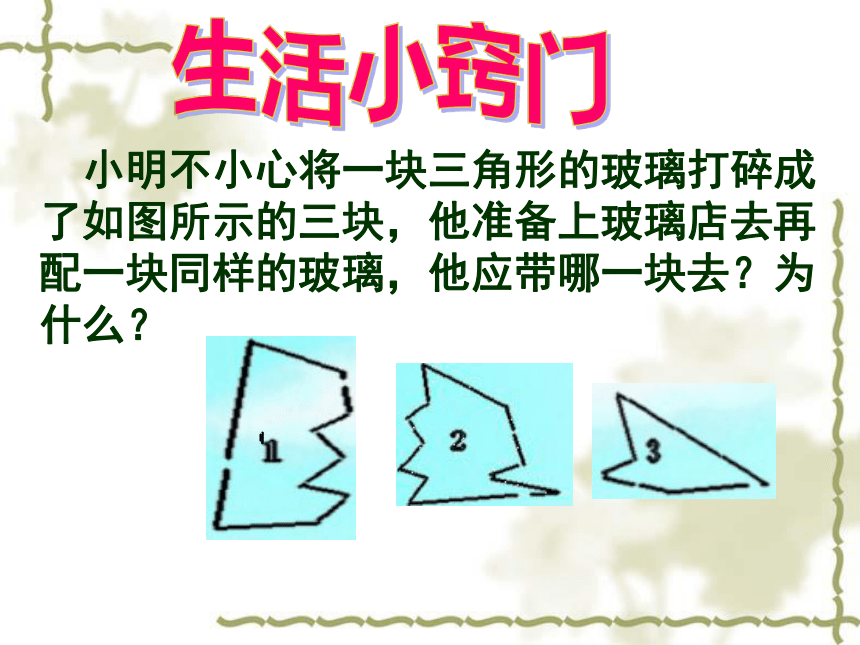
课件33张PPT。第十三章 三角形三角形全等的条件(复习)温中实验学校 钟凌峰生活小窍门 小明不小心将一块三角形的玻璃打碎成了如图所示的三块,他准备上玻璃店去再配一块同样的玻璃,他应带哪一块去?为什么?
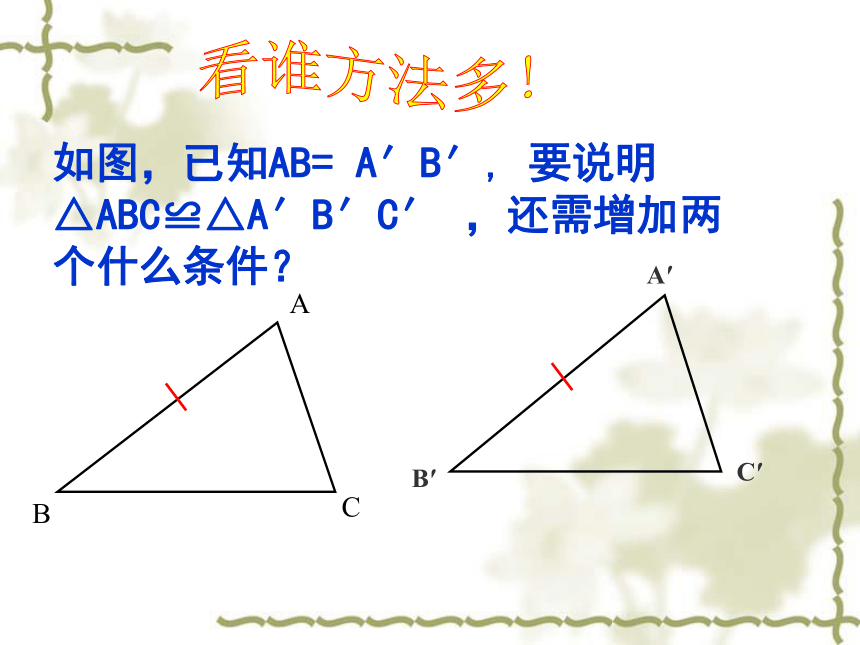
如图,已知AB= A′B′, 要说明△ABC≌△A′B′C′ ,还需增加两个什么条件?
?
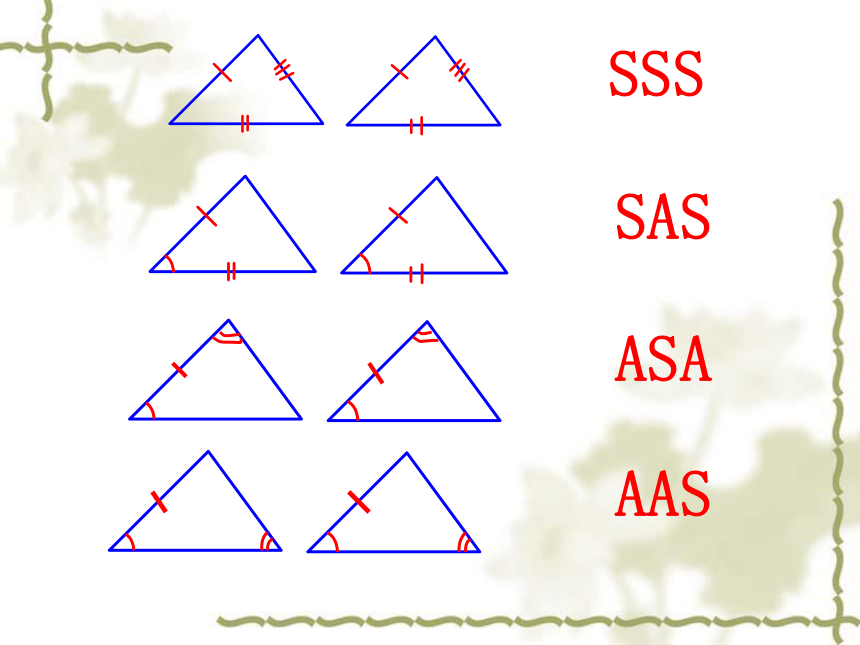
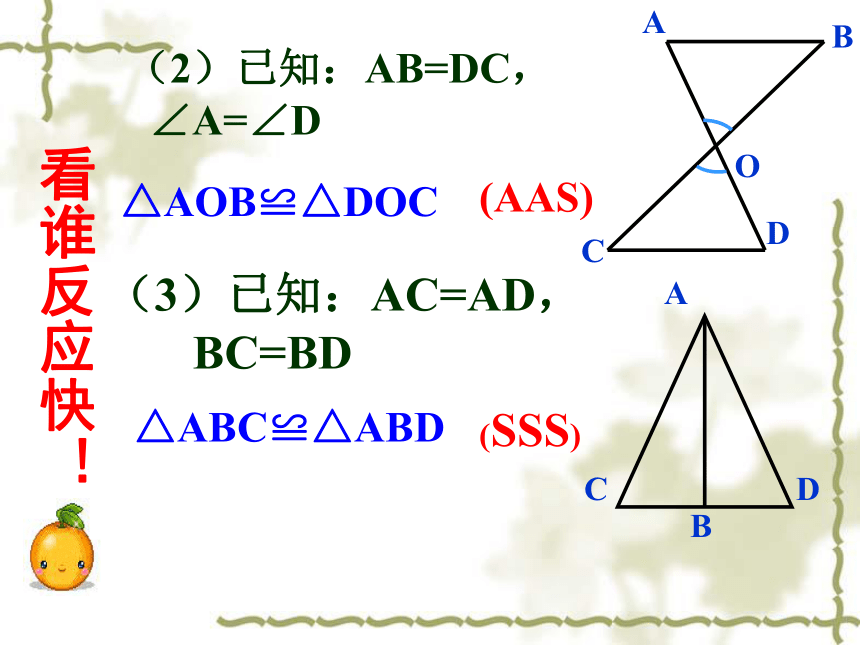
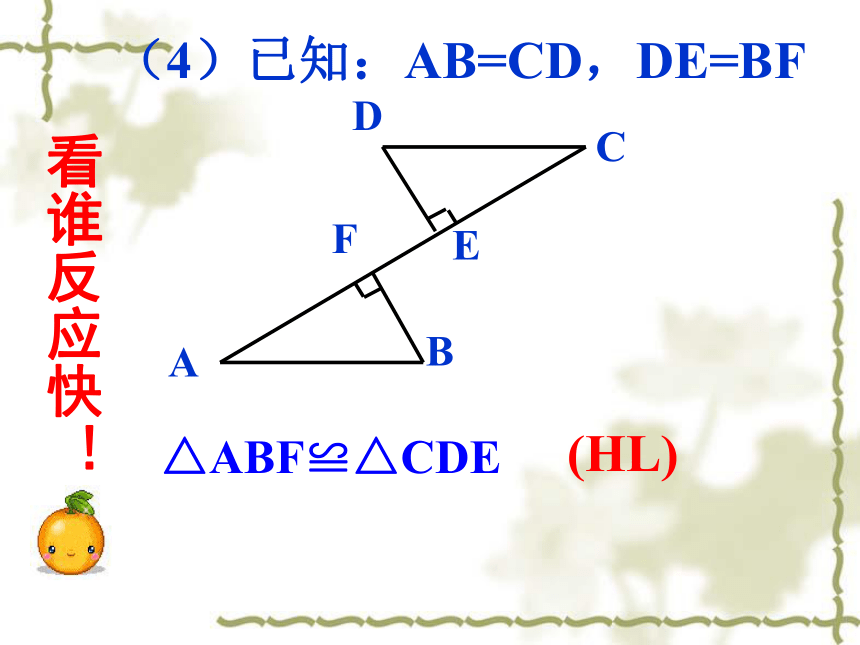
A′C′B′CBA看谁方法多!SSSSASASAAAS三角形全等的条件:①一般三角形全等的条件:SAS、ASA、AAS、SSS②直角三角形全等的条件: SAS、ASA、AAS、SSS、HL知识点(4)已知:AB=CD,DE=BF (HL) △ABF≌△CDE 看谁反应快!练一练1.已知: △ABC和△ A′B′C′中,AB=A′B′,
∠A=∠A′,∠B=∠B′,
则△ABC≌△ A′B′C′的根据是( )
A; SAS B: ASA C: AAS D:都不对
BD2.已知: △ABC和△A′B′C ′中,AB=A′B′,
∠A=∠A′, 若△ABC≌△ A′B′C′,
还需要什么条件( )
A:∠B=∠B′ B: ∠C=∠C′
C: AC=A′C′ D: A、B、C均可
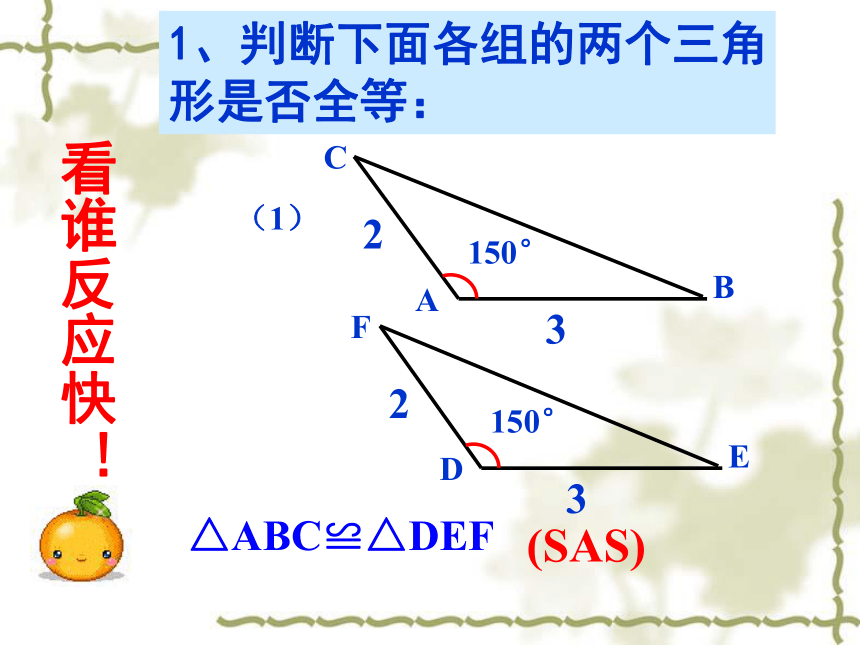
看谁反应快!看谁反应快!看谁反应快!看谁反应快!45、如图,下列条件,可以判定△ABC≌△DEF的是( )C A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,AC=DF 看谁反应快!判断题:
1、有两角和一边对应相等的两个三角形全等。( )
2、有两角和其中一角的平分线对应相等的两个三角形全等( )
填空题:
1、如图,AD交BC于O,AB∥CD且AB=CD,那么AO= , BO= ,
2、若△ABC的∠B=∠C, △ A′B′C′的∠ B′=
∠ C′,且BC= B′C′,那么△ABC与△ A′B′C′全等吗? 。(1图)√√DOCO不一定全等例1:如图:已知C是AB的中点,∠A=∠B,AD=BE,MD=NE.
求证:△ADC≌△BEC, △MEC≌△NDC例2问题1 已知:如图,AB=DE,AC=DF,
BE=CF,求证:∠A=∠D问题2、已知:如图∠1= ∠2, ∠ABC= ∠DCB。AC、DB 相交于点O。
求证:AB=DCABCDO343.如图,∠1=∠2,∠3=∠4求证:AC=ADABDABCABDABC∠1=∠2已知AB=AB∠ABD=∠ABC已知ABDABCASAAC=AD4.如图,BE∥DF,∠B=∠D,AE=CF,那么,△ADF和△CBE全等吗?ADECFB5ABCDE12 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?解: △ABC和△ADE全等。 ∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC ∴ △ABC≌△ADE(AAS)在△ABC和△ADC 中即∠BAC=∠DAE =(已知)ADAB更上一层楼1.已知 :如图, AB=DB , ∠1=∠2,只需添加一个条件,就可得到△ABC≌△DBE.你有几种办法?
开放练习2.如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?3.已知:如图,点D、E在△ABC的边BC上,AB=AC,∠B=∠C,要证明△ABE≌△ACD,只要补充一个条件,应补充什么条件?___________
(说明:图中不需要再添辅助线和其他字母,把可补充的条件用符号写在规定的横线上,并说明理由)ABDEC4.已知,如图,AD∥BC,AD=BC,AE=CF,
求证:DE∥BFABCDEF要证明相等的线段或角分别在两组以上的可能全等的三角形中,就应分析在哪对三角形中最好,一般我们选用具备条件多的一对三角形证明5.小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,小明不用测量就能知道EH=FH吗?说明理由。EFDH根据“SAS” △EDH≌△FDH 所以EH=FH连接EF,那么EF⊥DH吗?说明理由 这位聪明的八路军战士的方法如下: 战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。ACBD你觉得他测得的距离准确吗?说明其中的理由。趣味生活∴BC= DC( )ACBD理由:在△ACB与△ACD中,∠BAC=∠DACAC=AC(公共边) ∠ACB=∠ACD=90°△ACB≌△ACD(ASA)全等三角形的对应边相等趣味生活 2.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?趣味生活
感悟与反思通过本节课学习你有什么收获?
如图,已知AB= A′B′, 要说明△ABC≌△A′B′C′ ,还需增加两个什么条件?
?
A′C′B′CBA看谁方法多!SSSSASASAAAS三角形全等的条件:①一般三角形全等的条件:SAS、ASA、AAS、SSS②直角三角形全等的条件: SAS、ASA、AAS、SSS、HL知识点(4)已知:AB=CD,DE=BF (HL) △ABF≌△CDE 看谁反应快!练一练1.已知: △ABC和△ A′B′C′中,AB=A′B′,
∠A=∠A′,∠B=∠B′,
则△ABC≌△ A′B′C′的根据是( )
A; SAS B: ASA C: AAS D:都不对
BD2.已知: △ABC和△A′B′C ′中,AB=A′B′,
∠A=∠A′, 若△ABC≌△ A′B′C′,
还需要什么条件( )
A:∠B=∠B′ B: ∠C=∠C′
C: AC=A′C′ D: A、B、C均可
看谁反应快!看谁反应快!看谁反应快!看谁反应快!45、如图,下列条件,可以判定△ABC≌△DEF的是( )C A、∠A=∠D,∠B=∠E,∠C=∠F
B、AB=DE,∠B=∠E,AC=DF
C、∠A=∠D,∠B=∠E,AC=DF 看谁反应快!判断题:
1、有两角和一边对应相等的两个三角形全等。( )
2、有两角和其中一角的平分线对应相等的两个三角形全等( )
填空题:
1、如图,AD交BC于O,AB∥CD且AB=CD,那么AO= , BO= ,
2、若△ABC的∠B=∠C, △ A′B′C′的∠ B′=
∠ C′,且BC= B′C′,那么△ABC与△ A′B′C′全等吗? 。(1图)√√DOCO不一定全等例1:如图:已知C是AB的中点,∠A=∠B,AD=BE,MD=NE.
求证:△ADC≌△BEC, △MEC≌△NDC例2问题1 已知:如图,AB=DE,AC=DF,
BE=CF,求证:∠A=∠D问题2、已知:如图∠1= ∠2, ∠ABC= ∠DCB。AC、DB 相交于点O。
求证:AB=DCABCDO343.如图,∠1=∠2,∠3=∠4求证:AC=ADABDABCABDABC∠1=∠2已知AB=AB∠ABD=∠ABC已知ABDABCASAAC=AD4.如图,BE∥DF,∠B=∠D,AE=CF,那么,△ADF和△CBE全等吗?ADECFB5ABCDE12 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?解: △ABC和△ADE全等。 ∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC ∴ △ABC≌△ADE(AAS)在△ABC和△ADC 中即∠BAC=∠DAE =(已知)ADAB更上一层楼1.已知 :如图, AB=DB , ∠1=∠2,只需添加一个条件,就可得到△ABC≌△DBE.你有几种办法?
开放练习2.如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?3.已知:如图,点D、E在△ABC的边BC上,AB=AC,∠B=∠C,要证明△ABE≌△ACD,只要补充一个条件,应补充什么条件?___________
(说明:图中不需要再添辅助线和其他字母,把可补充的条件用符号写在规定的横线上,并说明理由)ABDEC4.已知,如图,AD∥BC,AD=BC,AE=CF,
求证:DE∥BFABCDEF要证明相等的线段或角分别在两组以上的可能全等的三角形中,就应分析在哪对三角形中最好,一般我们选用具备条件多的一对三角形证明5.小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,小明不用测量就能知道EH=FH吗?说明理由。EFDH根据“SAS” △EDH≌△FDH 所以EH=FH连接EF,那么EF⊥DH吗?说明理由 这位聪明的八路军战士的方法如下: 战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。ACBD你觉得他测得的距离准确吗?说明其中的理由。趣味生活∴BC= DC( )ACBD理由:在△ACB与△ACD中,∠BAC=∠DACAC=AC(公共边) ∠ACB=∠ACD=90°△ACB≌△ACD(ASA)全等三角形的对应边相等趣味生活 2.如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别 沿两条直线行走,并同时到达D,E两地,DA⊥AB,EB⊥AB,D,E与路段AB的距离相等吗?为什么?趣味生活
感悟与反思通过本节课学习你有什么收获?
