人教版八年级数学上册13.3.2等边三角形 第2课时教学课件(共24张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3.2等边三角形 第2课时教学课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
等边三角形
(第二课时)
课前准备
两个含角的三角尺.
等边三角形
性 质
判 定
复习回顾:等边三角形的性质和判定
. 三条边相等
. 三个内角都相等,都为 .
. “三线合一”
. 轴对称图形( 条对称轴)
. 定义(三条边相等)
. 三个角相等
. 有一个角是 的等腰三角形
复习回顾:等边三角形的性质和判定与边角关系
等边三角形
性 质
判 定
. 三条边相等
. 三个内角都相等,都为 .
. “三线合一”
. 轴对称图形( 条对称轴)
. 定义(三条边相等)
. 三个角相等
. 有一个角是 的等腰三角形
动手实践,探究新知
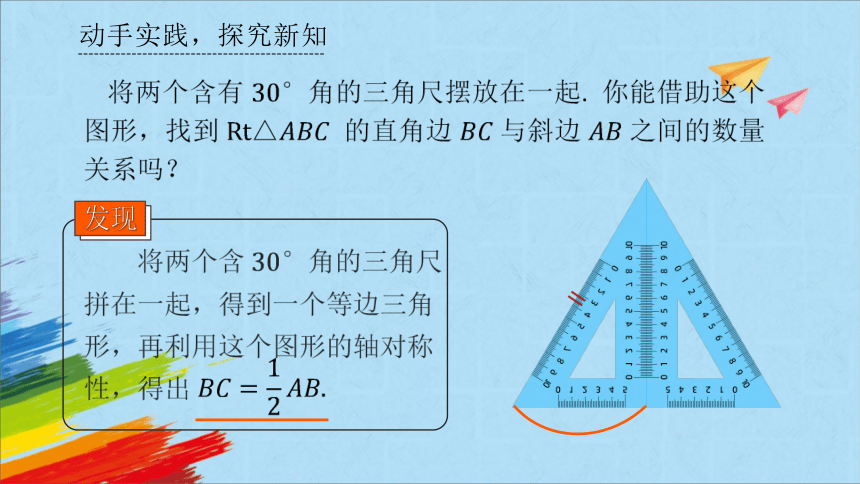
将两个含有 角的三角尺摆放在一起. 你能借助这个图形,找到 △ 的直角边 与斜边 之间的数量关系吗?
将两个含角的三角尺拼在一起,得到一个等边三角形,再利用这个图形的轴对称性,得出
发现
动手实践,探究新知
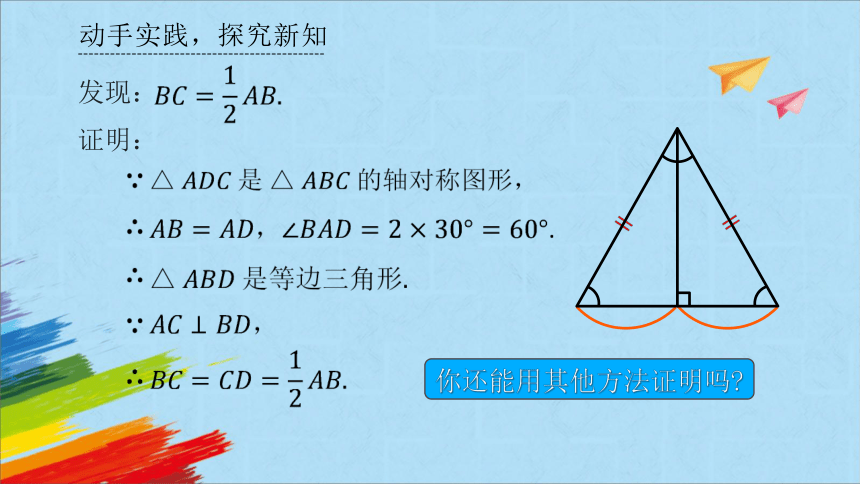
证明:
发现:
的轴对称图形,
.
你还能用其他方法证明吗
动手实践,探究新知
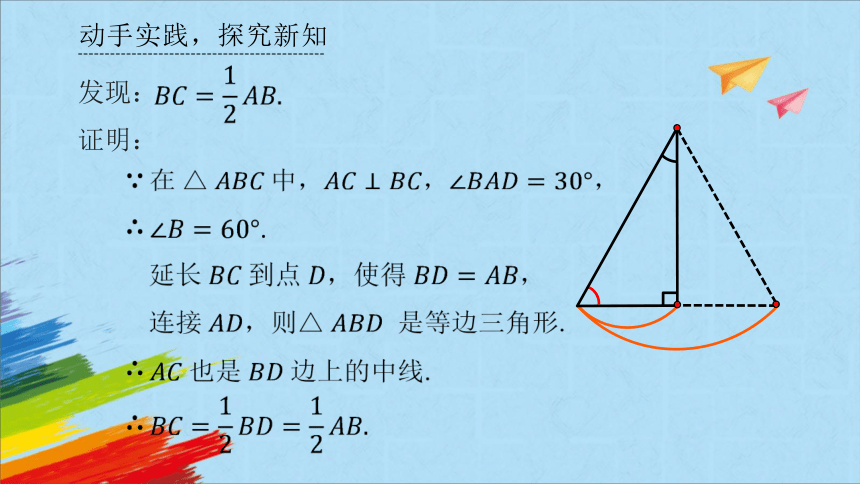
证明:
发现:
,
.
.
延长 到点,使得,
连接,则 是等边三角形.
含 角的直角三角形的性质
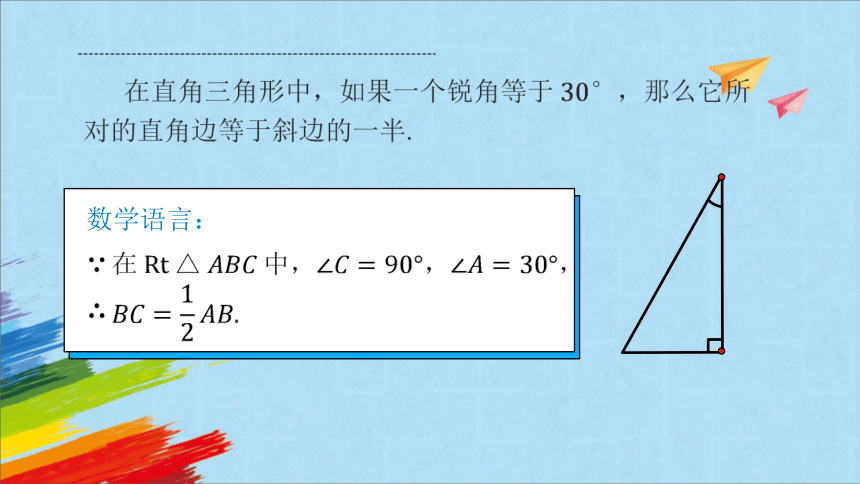
数学语言:
在直角三角形中,如果一个锐角等于,那么它所对的直角边等于斜边的一半.
,
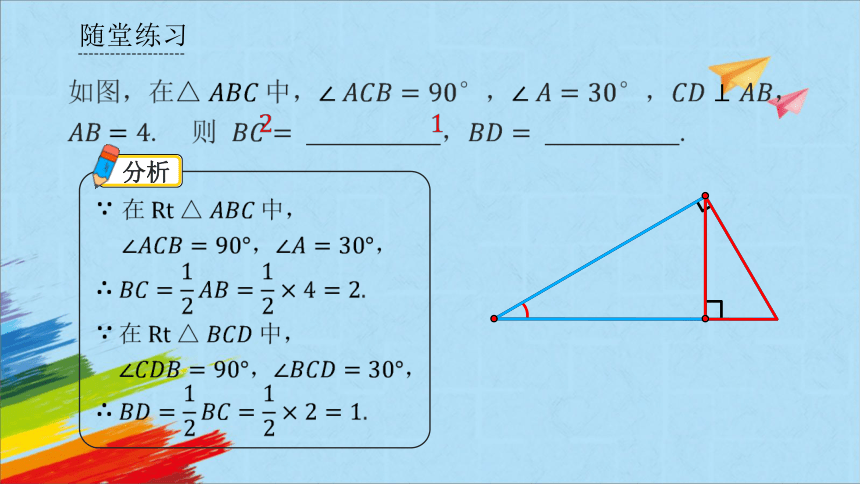
随堂练习
如图,在中,, ,, . 则 , .
,
,
分析
随堂练习
小明沿倾斜角为 的山坡从山脚步行到山顶,共走了 ,山的高度为 .
含 的角的直角三角形的性质的应用.
分析
下图是屋架设计图的一部分,点是斜梁 的中点,立柱, 垂直于横梁,,立柱 , 要多长?
例
分析
例
,
解:
又
答:立柱 的长是 ,的长是 .
巩固提高
三角形三个角的度数之比为 ,
三角形三个角的度数之比为 ,它的最大边长等于 ,则最小边长是 .
分析
巩固提高
三角形三个角的度数之比为 ,它的最大边长等于 ,则最小边长是 .
最大边长等于 ,
分析
巩固提高
分析
如图,在 中,,, 是 的中点,. 则 .
巩固提高
如图,在 中,,, 是 的中点,. 则 .
,
分析
分析
巩固提高
如图, 中,,, 为 的垂直平分线, 交 于 ,交 于 ,,求 的长.
分析
线段的垂直平分线的性质.
巩固提高
如图, 中,,, 为 的垂直平分线, 交 于 ,交 于 ,,求 的长.
分析
巩固提高
解:
课
堂
小
结
由等边三角形推出含 角的直角三角形的性质,反映直角三角形的边角关系.
增强对特殊直角三角形的认识,培养几何直观、推理能力.
课后作业
米
米
米
米
如图,一棵树在一次强台风中于离地面 米处折断倒下,倒下部分与地面成角,这棵树在折断前的高度为( ).
课后作业
如图,在,, 平分,若,则 等于( ).
课后作业
如图,在,,平分线 交于点 ,交 于点,若 ,则 的长为 .
课后作业
如图,在,平分交 于点,过点 作于点.
求证:△△.
若,,求 的长.
等边三角形
(第二课时)
课前准备
两个含角的三角尺.
等边三角形
性 质
判 定
复习回顾:等边三角形的性质和判定
. 三条边相等
. 三个内角都相等,都为 .
. “三线合一”
. 轴对称图形( 条对称轴)
. 定义(三条边相等)
. 三个角相等
. 有一个角是 的等腰三角形
复习回顾:等边三角形的性质和判定与边角关系
等边三角形
性 质
判 定
. 三条边相等
. 三个内角都相等,都为 .
. “三线合一”
. 轴对称图形( 条对称轴)
. 定义(三条边相等)
. 三个角相等
. 有一个角是 的等腰三角形
动手实践,探究新知
将两个含有 角的三角尺摆放在一起. 你能借助这个图形,找到 △ 的直角边 与斜边 之间的数量关系吗?
将两个含角的三角尺拼在一起,得到一个等边三角形,再利用这个图形的轴对称性,得出
发现
动手实践,探究新知
证明:
发现:
的轴对称图形,
.
你还能用其他方法证明吗
动手实践,探究新知
证明:
发现:
,
.
.
延长 到点,使得,
连接,则 是等边三角形.
含 角的直角三角形的性质
数学语言:
在直角三角形中,如果一个锐角等于,那么它所对的直角边等于斜边的一半.
,
随堂练习
如图,在中,, ,, . 则 , .
,
,
分析
随堂练习
小明沿倾斜角为 的山坡从山脚步行到山顶,共走了 ,山的高度为 .
含 的角的直角三角形的性质的应用.
分析
下图是屋架设计图的一部分,点是斜梁 的中点,立柱, 垂直于横梁,,立柱 , 要多长?
例
分析
例
,
解:
又
答:立柱 的长是 ,的长是 .
巩固提高
三角形三个角的度数之比为 ,
三角形三个角的度数之比为 ,它的最大边长等于 ,则最小边长是 .
分析
巩固提高
三角形三个角的度数之比为 ,它的最大边长等于 ,则最小边长是 .
最大边长等于 ,
分析
巩固提高
分析
如图,在 中,,, 是 的中点,. 则 .
巩固提高
如图,在 中,,, 是 的中点,. 则 .
,
分析
分析
巩固提高
如图, 中,,, 为 的垂直平分线, 交 于 ,交 于 ,,求 的长.
分析
线段的垂直平分线的性质.
巩固提高
如图, 中,,, 为 的垂直平分线, 交 于 ,交 于 ,,求 的长.
分析
巩固提高
解:
课
堂
小
结
由等边三角形推出含 角的直角三角形的性质,反映直角三角形的边角关系.
增强对特殊直角三角形的认识,培养几何直观、推理能力.
课后作业
米
米
米
米
如图,一棵树在一次强台风中于离地面 米处折断倒下,倒下部分与地面成角,这棵树在折断前的高度为( ).
课后作业
如图,在,, 平分,若,则 等于( ).
课后作业
如图,在,,平分线 交于点 ,交 于点,若 ,则 的长为 .
课后作业
如图,在,平分交 于点,过点 作于点.
求证:△△.
若,,求 的长.
