人教版八年级数学上册13.3.1等腰三角形 第3课时教学课件(共52张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3.1等腰三角形 第3课时教学课件(共52张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 17:26:32 | ||
图片预览



文档简介
(共52张PPT)
等腰三角形
(第三课时)
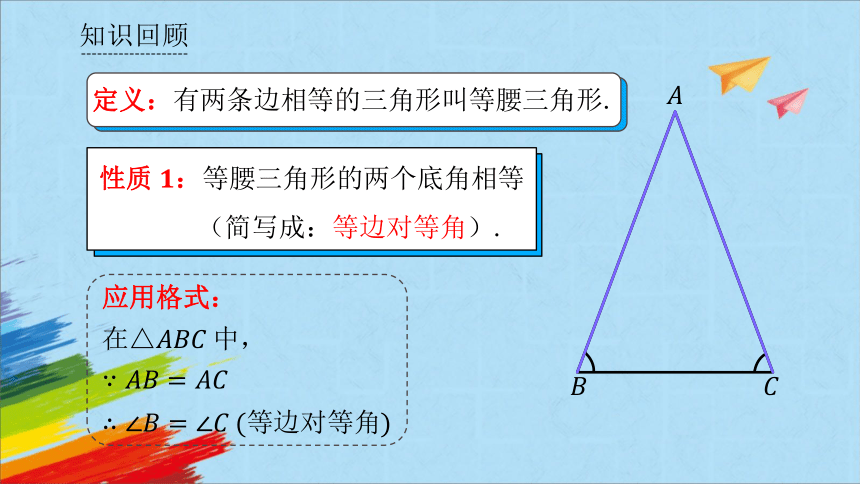
性质:等腰三角形的两个底角相等
(简写成:等边对等角).
定义:有两条边相等的三角形叫等腰三角形.
应用格式:
在△中,
等边对等角
知识回顾
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(简写成:三线合一).
性质:
应用格式:
,
三线合一
知识回顾
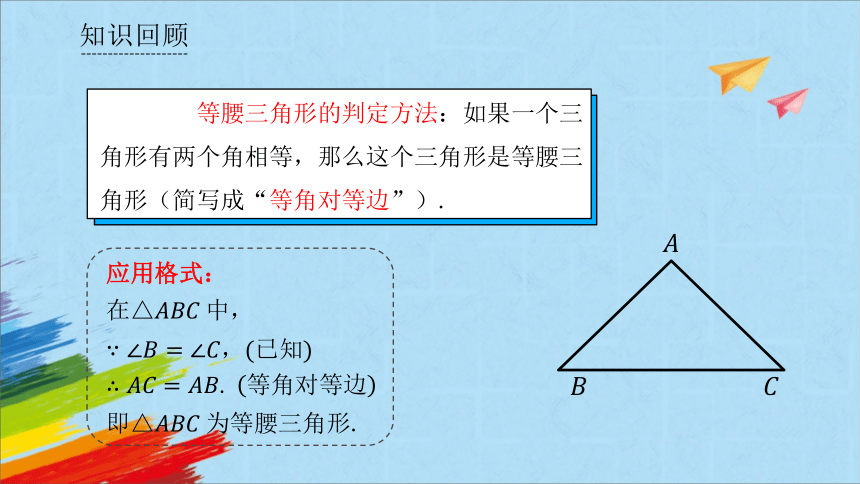
等腰三角形的判定方法:如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
应用格式:
在△中,
.
即△等腰三角形.
知识回顾
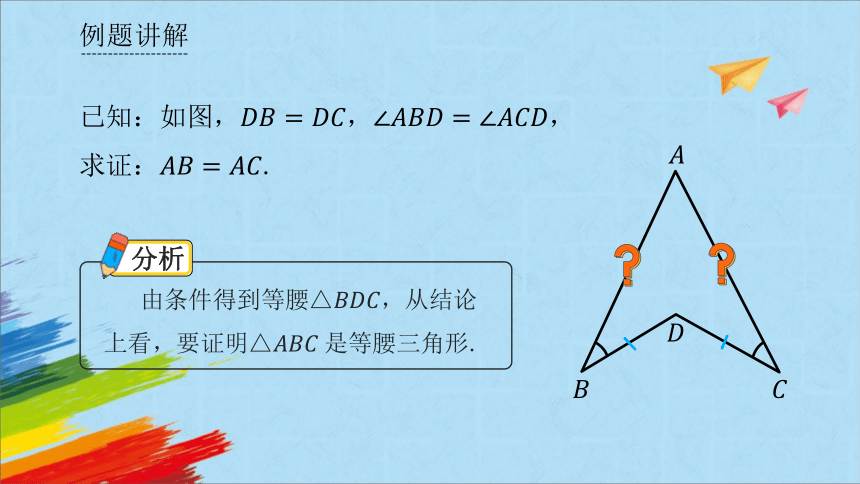
已知:如图,,,
求证:.
例题讲解
由条件得到等腰△,从结论上看,要证明△是等腰三角形.
分析
例题讲解
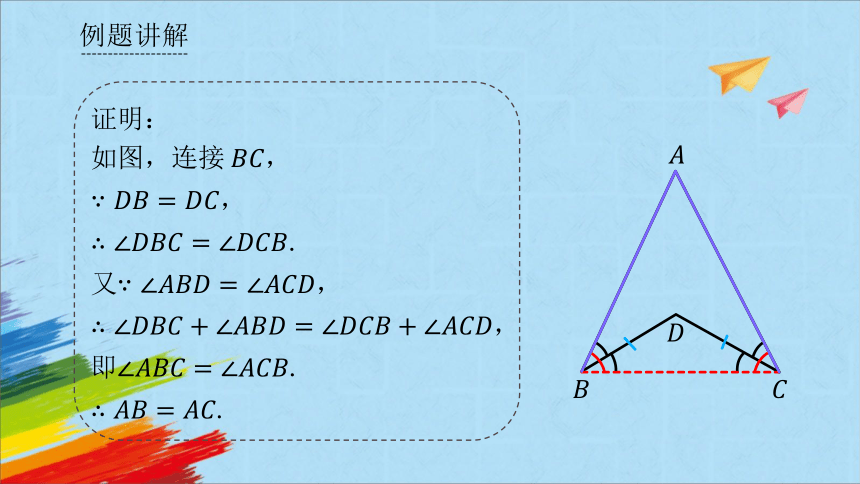
如图,连接,
,
.
又,
,
即.
.
证明:
练习
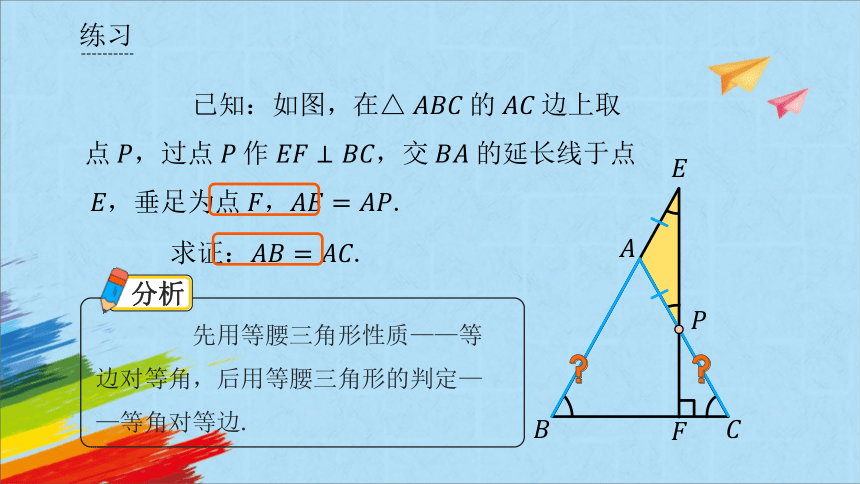
已知:如图,在△的边上取点,过点作,交的延长线于点,垂足为点,.
求证.
先用等腰三角形性质——等边对等角,后用等腰三角形的判定——等角对等边.
分析
练习
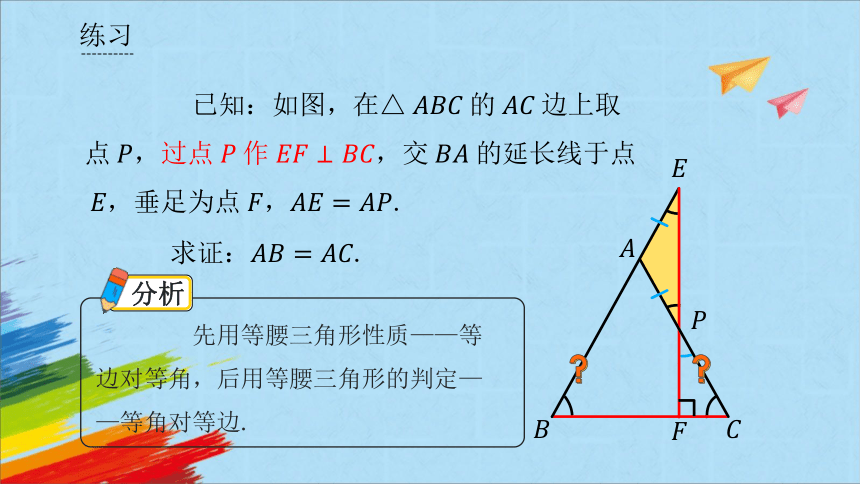
已知:如图,在△的边上取点,过点作,交的延长线于点,垂足为点,.
求证.
先用等腰三角形性质——等边对等角,后用等腰三角形的判定——等角对等边.
分析
练习
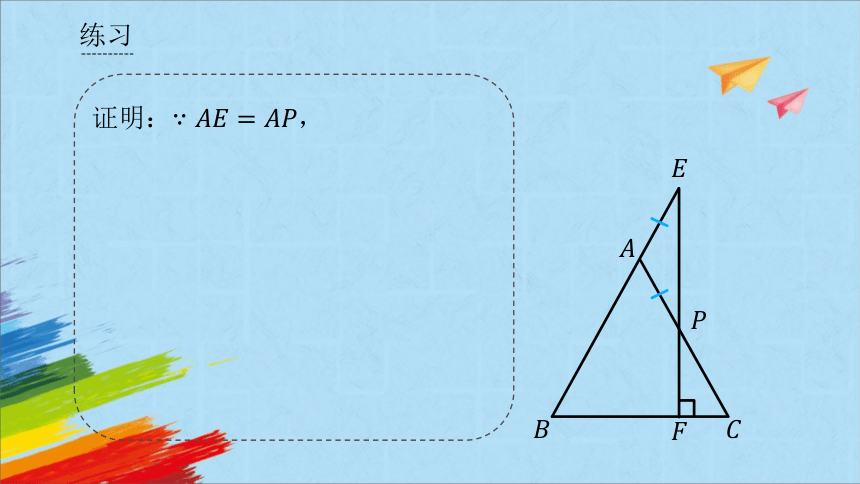
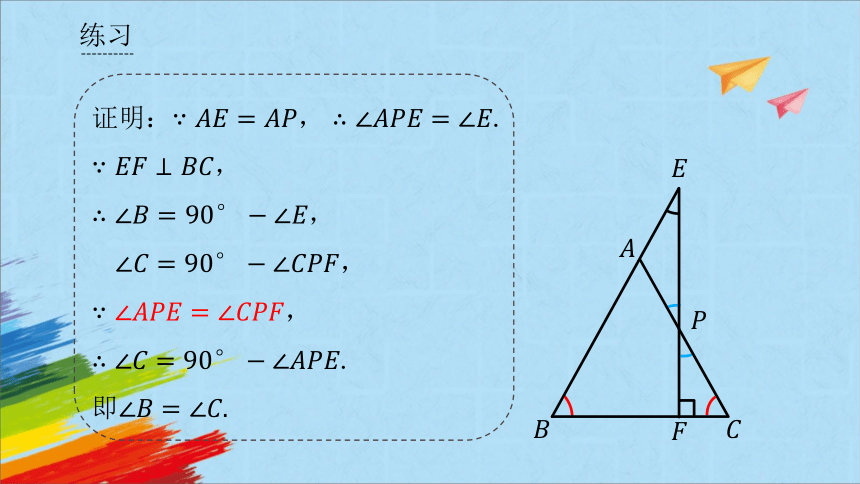
证明:
练习
证明:.
,
,
,
练习
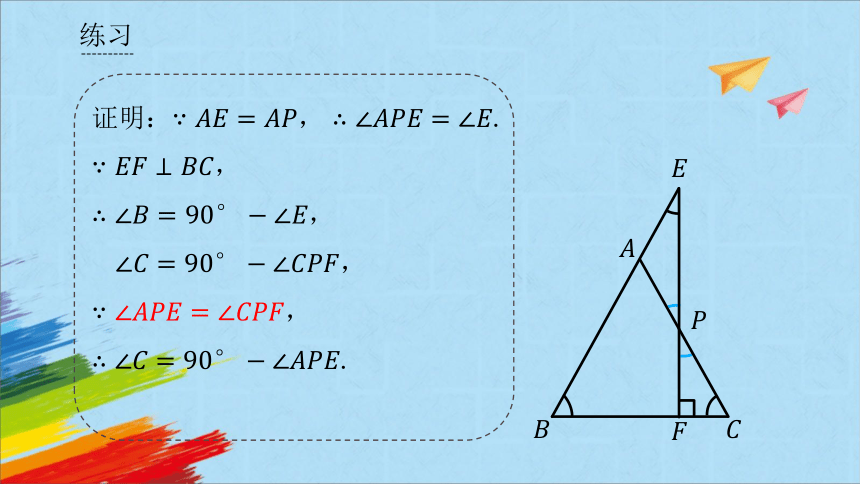
证明:.
,
,
,
,
.
练习
证明:.
,
,
,
,
.
即
练习
证明:.
,
,
,
,
.
即.
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
高
中线
角平分线
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
解:∥
,
,
,
,
,
是等腰三角形.
.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
例题讲解
高
中线
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
三线合一
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
方法一:通过证全等得对应线段相等,
用定义即可;
方法二:角平分线加平行出等腰.
分析
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
方法一:通过证全等得对应线段相等,
用定义即可;
方法二:角平分线加平行出等腰.
分析
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
方法一:通过证全等得对应线段相等,
用定义即可;
方法二:角平分线加平行出等腰.
分析
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
方法一:通过证全等得对应线段相等,
用定义即可;
方法二:角平分线加平行出等腰.
分析
解方法一
重合部分是等腰三角形. 理由如下:
根据轴对称的性质可得
,
练习
练习
解方法一
重合部分是等腰三角形. 理由如下:
根据轴对称的性质可得
,
又,
解方法一
重合部分是等腰三角形. 理由如下:
根据轴对称的性质可得
,
又,
,
部分是等腰三角形.
练习
练习
方法二:根据轴对称性得,
∵ ∥
.
.
.
部分是等腰三角形.
例题讲解
已知等腰三角形的底边长,腰上的高,请画出符合条件的等腰三角形.
画草图
例题讲解
画草图
已知等腰三角形的底边长,腰上的高,请画出符合条件的等腰三角形.
例题讲解
作法
作线段= ,过点作直线于点.
在直线 上找一点使得
= (以为圆心,为半径画弧交于点).
1
2
例题讲解
作法
作的垂直平分线交直线于点 . 连接.
则△即为所求.
3
课
堂
小
结
1
确定等腰三角形的依据.
1
定义;
2
等角对等边.
注意以下两种情形
1
当图形中有角平分线和平行线时常常有等腰三角形;
2
当图中出现线段的垂直平分线时常常有等腰三角形.
课
堂
小
结
2
注意性质和判定的转换.
1
画草图
2
分析草图
3
解决画图问题的一般步骤:
3
按顺序画图
课后作业
A.
C.
B.
D.
如图,在△中,和的平分线相交于点,过点作∥,分别交于,于点,. 若
,则线段的长为( ).
1
课后作业
如图,,为延长线上一点,作于,交于点,求证:△为等腰三角形.
2
已知等腰三角形的腰长,腰上请画出符合条件的等腰三角形.
3
等腰三角形
(第三课时)
性质:等腰三角形的两个底角相等
(简写成:等边对等角).
定义:有两条边相等的三角形叫等腰三角形.
应用格式:
在△中,
等边对等角
知识回顾
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(简写成:三线合一).
性质:
应用格式:
,
三线合一
知识回顾
等腰三角形的判定方法:如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角对等边”).
应用格式:
在△中,
.
即△等腰三角形.
知识回顾
已知:如图,,,
求证:.
例题讲解
由条件得到等腰△,从结论上看,要证明△是等腰三角形.
分析
例题讲解
如图,连接,
,
.
又,
,
即.
.
证明:
练习
已知:如图,在△的边上取点,过点作,交的延长线于点,垂足为点,.
求证.
先用等腰三角形性质——等边对等角,后用等腰三角形的判定——等角对等边.
分析
练习
已知:如图,在△的边上取点,过点作,交的延长线于点,垂足为点,.
求证.
先用等腰三角形性质——等边对等角,后用等腰三角形的判定——等角对等边.
分析
练习
证明:
练习
证明:.
,
,
,
练习
证明:.
,
,
,
,
.
练习
证明:.
,
,
,
,
.
即
练习
证明:.
,
,
,
,
.
即.
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
高
中线
角平分线
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
以平行线为桥梁,运用等腰三角形的性质和判定;
运用三线合一以及垂直平分线性质.
分析
1
2
在等腰△中,,是边上的高,分别是边上的点. ∥.
说明△是等腰三角形;
说明△是等腰三角形.
例题讲解
解:∥
,
,
,
,
,
是等腰三角形.
.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
例题讲解
高
中线
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
例题讲解
三线合一
解:是等腰的底边上的高,
也是的平分线.
是等腰三角形,
是底边上的高和中线
是线段的垂直平分线.
,所以△是等腰三角形.
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
方法一:通过证全等得对应线段相等,
用定义即可;
方法二:角平分线加平行出等腰.
分析
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
方法一:通过证全等得对应线段相等,
用定义即可;
方法二:角平分线加平行出等腰.
分析
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
方法一:通过证全等得对应线段相等,
用定义即可;
方法二:角平分线加平行出等腰.
分析
练习
如图所示,把一张长方形的纸沿对角线折叠,则重合部分是等腰三角形吗?为什么?
方法一:通过证全等得对应线段相等,
用定义即可;
方法二:角平分线加平行出等腰.
分析
解方法一
重合部分是等腰三角形. 理由如下:
根据轴对称的性质可得
,
练习
练习
解方法一
重合部分是等腰三角形. 理由如下:
根据轴对称的性质可得
,
又,
解方法一
重合部分是等腰三角形. 理由如下:
根据轴对称的性质可得
,
又,
,
部分是等腰三角形.
练习
练习
方法二:根据轴对称性得,
∵ ∥
.
.
.
部分是等腰三角形.
例题讲解
已知等腰三角形的底边长,腰上的高,请画出符合条件的等腰三角形.
画草图
例题讲解
画草图
已知等腰三角形的底边长,腰上的高,请画出符合条件的等腰三角形.
例题讲解
作法
作线段= ,过点作直线于点.
在直线 上找一点使得
= (以为圆心,为半径画弧交于点).
1
2
例题讲解
作法
作的垂直平分线交直线于点 . 连接.
则△即为所求.
3
课
堂
小
结
1
确定等腰三角形的依据.
1
定义;
2
等角对等边.
注意以下两种情形
1
当图形中有角平分线和平行线时常常有等腰三角形;
2
当图中出现线段的垂直平分线时常常有等腰三角形.
课
堂
小
结
2
注意性质和判定的转换.
1
画草图
2
分析草图
3
解决画图问题的一般步骤:
3
按顺序画图
课后作业
A.
C.
B.
D.
如图,在△中,和的平分线相交于点,过点作∥,分别交于,于点,. 若
,则线段的长为( ).
1
课后作业
如图,,为延长线上一点,作于,交于点,求证:△为等腰三角形.
2
已知等腰三角形的腰长,腰上请画出符合条件的等腰三角形.
3
