人教版八年级数学上册13.3.1等腰三角形 第2课时教学课件(共38张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3.1等腰三角形 第2课时教学课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 17:27:42 | ||
图片预览


文档简介
(共38张PPT)
等腰三角形
(第二课时)
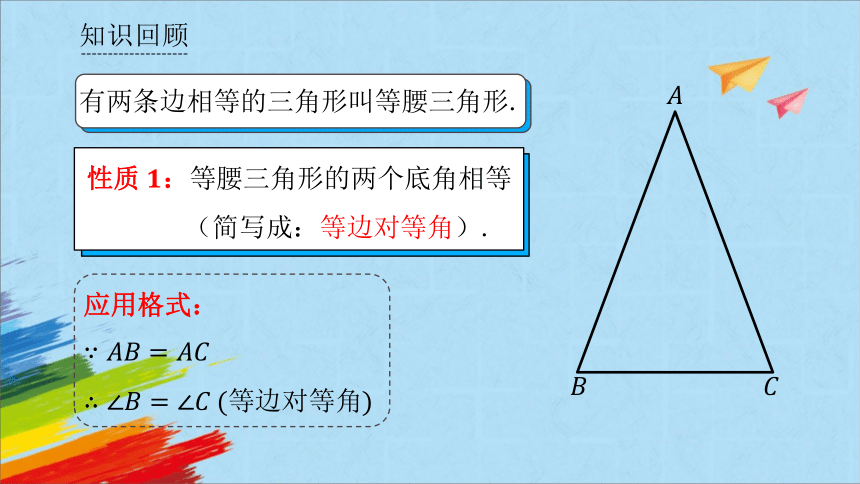
性质:等腰三角形的两个底角相等
(简写成:等边对等角).
有两条边相等的三角形叫等腰三角形.
应用格式:
等边对等角
知识回顾
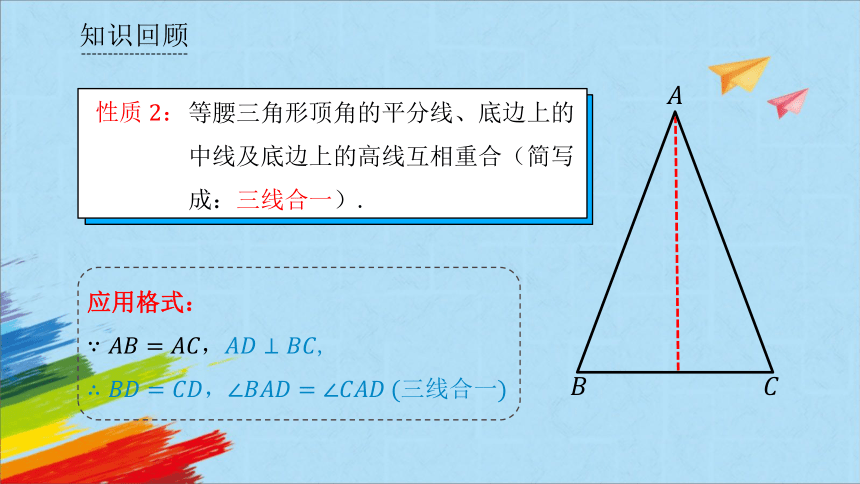
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(简写成:三线合一).
性质:
应用格式:
,
三线合一
知识回顾
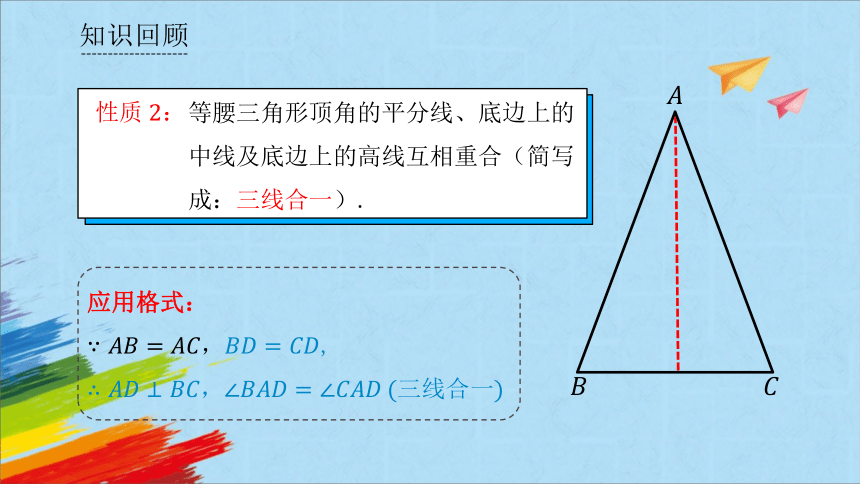
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(简写成:三线合一).
性质:
应用格式:
,
三线合一
知识回顾
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(简写成:三线合一).
性质:
应用格式:
,
三线合一
知识回顾
知识回顾
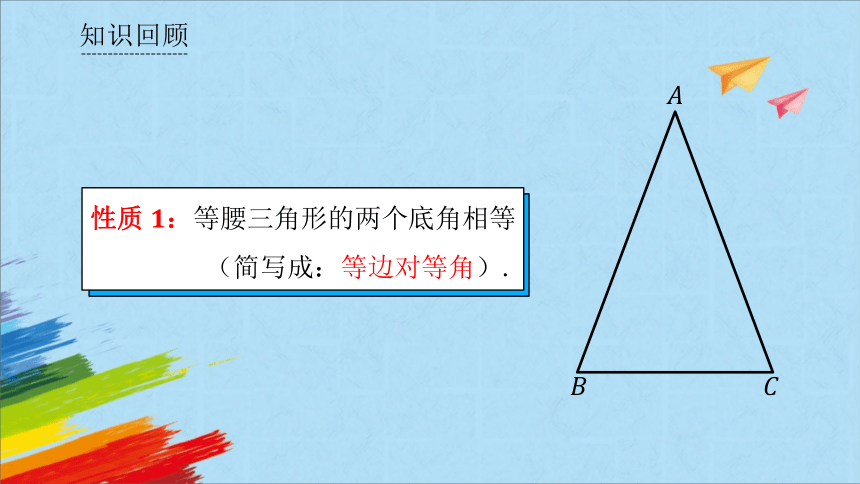
性质:等腰三角形的两个底角相等
(简写成:等边对等角).
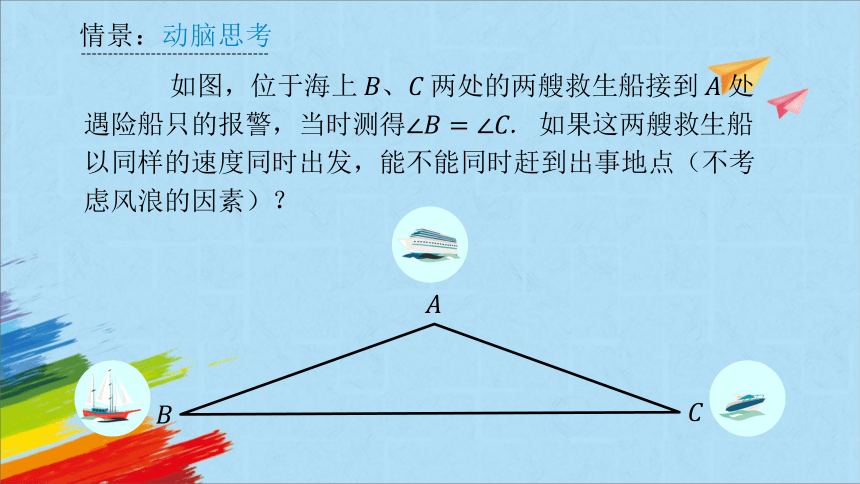
情景:动脑思考
如图,位于海上两处的两艘救生船接到处遇险船只的报警,当时测得. 如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪的因素)?
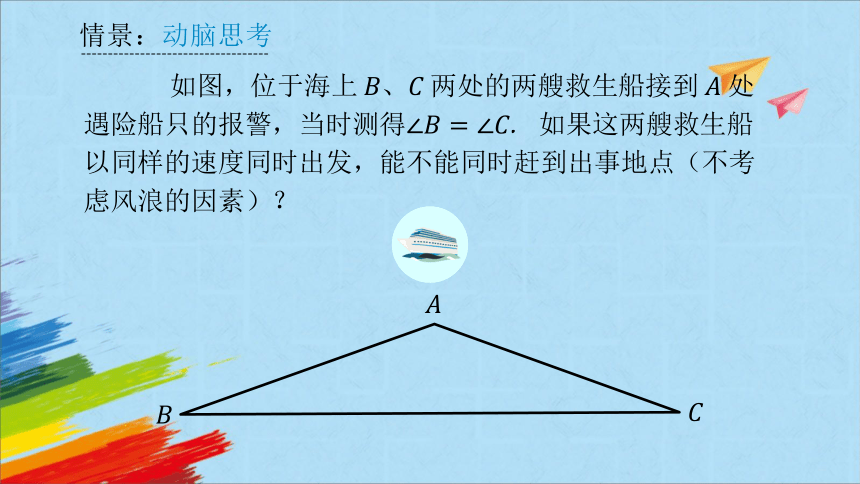
情景:动脑思考
如图,位于海上两处的两艘救生船接到处遇险船只的报警,当时测得. 如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪的因素)?
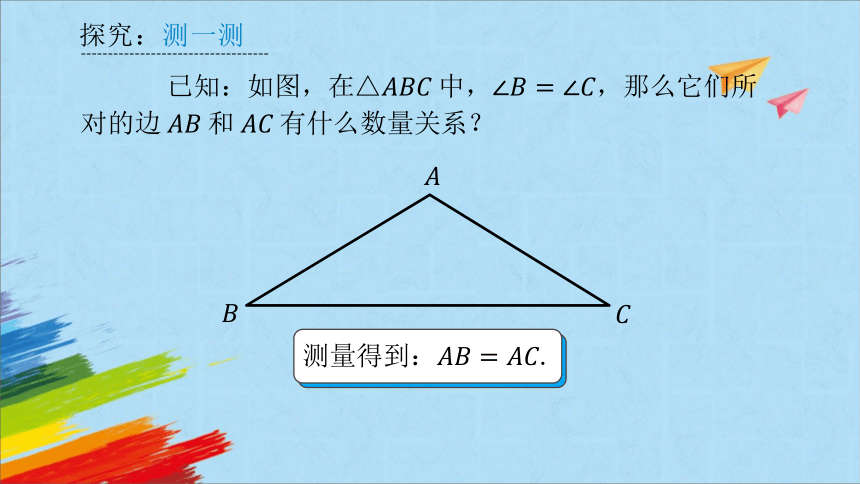
探究:测一测
已知:如图,在△中,那么它们所对的边和有什么数量关系?
测量得到:.
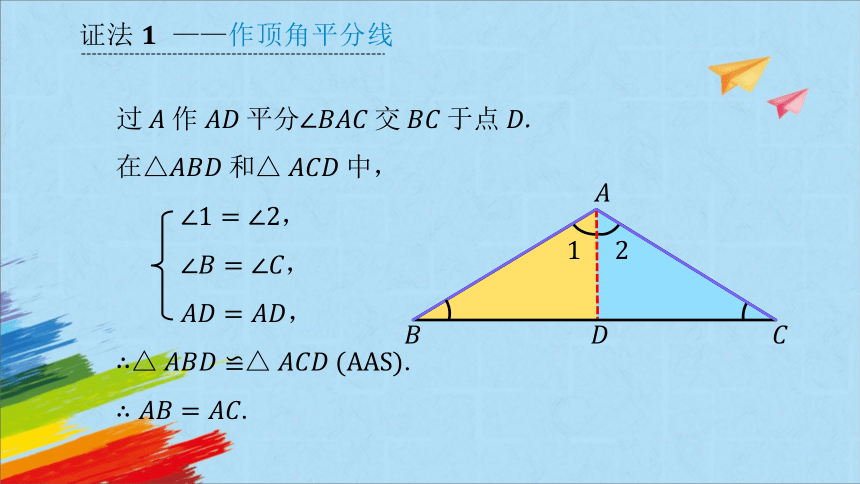
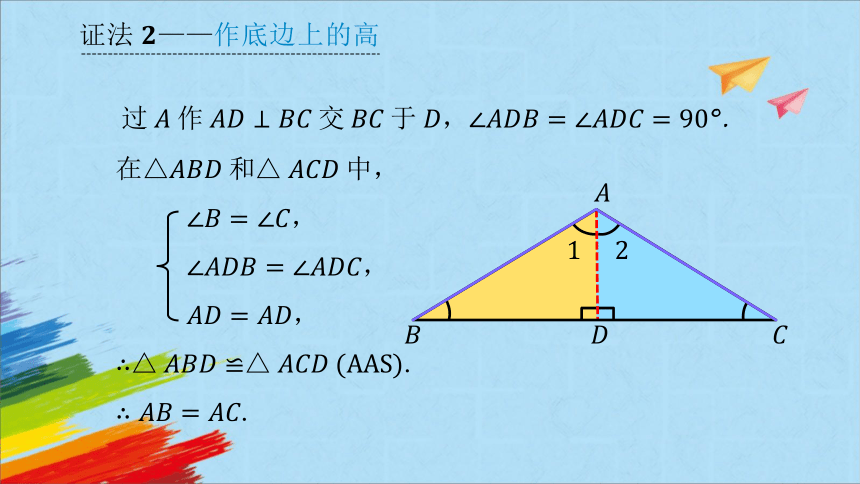
过作平分交于点.
证法 ——作顶角平分线
在△和中,
,
,
,
.
.
过作交于,.
在△和中,
,
,
,
.
.
证法——作底边上的高
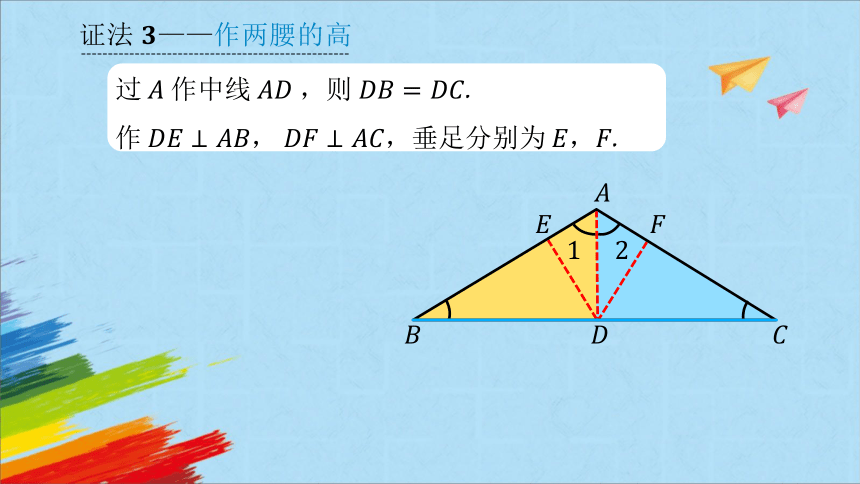
证法——作两腰的高
过作中线,则.
作,,垂足分别为,.
在△与中,
,
,
,
.
证法——作两腰的高
过作中线,则.
作,,垂足分别为,.
证法——作两腰的高
在△与中,
,
,
,
.
过作中线,则.
作,,垂足分别为,.
又,,
,
,
,
,
.
证法——作两腰的高
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角
对等边”).
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角
对等边”).
应用格式:
在中,
即为等腰三角形.
辨析
错,因为都不是在同一个三角形中.
例题
求证
如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知是△的外角,,∥.
求证: .
例题
求证
如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知是△的外角,,∥.
求证: .
例题
求证
如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知是△的外角,,∥.
求证: .
例题—证明
.
又,
.
.
两直线平行,同位角相等
两直线平行,内错角相等
等角对等边
例题—作图
已知等腰三角形底边长为,底边上的高的长为,求作这个等腰三角形.
点应该在底边的垂直平分线上.
例题—作图
作法:
.作线段.
.作线段的垂直平分线交点.
.在上取一点,使.
.连接和,则△即为所求.
课堂练习
已知:如图,∥,平分.
求证:.
课堂练习
已知:如图,∥,平分.
求证:.
课堂练习
已知:如图,∥,平分.
求证:.
课堂练习
已知:如图,∥,平分.
求证:.
证明:∥,
.
课堂练习
已知:如图,∥,平分.
求证:.
证明:∥,
.
平分,
课堂练习
已知:如图,∥,平分.
求证:.
证明:∥,
.
平分,
.
课
堂
小
结
知识内容
等腰三角形的判定:
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
课
堂
小
结
教学方法
判定线段之间的数量关系,一般做法是通过全等或利用“等角对等边”,运用转化思想,解决问题.
比较等腰三角形的性质和判定:
“等边对等角”与“等角对等边”,条件与结论是对调的,运用逆向思维观察和思考,可以提升自己的理性思维.
课后作业
三角形
三角形
三角形
三角形
一个三角形的一个外角为,且它恰好等于一个不相邻的内角的倍,这个三角形是( ).
1
课后作业
一个三角形的一个外角为,且它恰好等于一个不相邻的内角的倍,这个三角形是( ).
1
三角形
三角形
三角形
三角形
课后作业
如图,已知,则______,图中的等腰三角形有________.
2
课后作业
如图,已知,则______,图中的等腰三角形有________.
2
课后作业
已知:如图,,和相交于点.
求证:△是等腰三角形.
3
课后作业
如图,上午时,一条船从处出发以每小时海里的速度向正北航行,中午时到达处,从、望灯塔,测得,,求从处到灯塔的距离.
4
北
等腰三角形
(第二课时)
性质:等腰三角形的两个底角相等
(简写成:等边对等角).
有两条边相等的三角形叫等腰三角形.
应用格式:
等边对等角
知识回顾
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(简写成:三线合一).
性质:
应用格式:
,
三线合一
知识回顾
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(简写成:三线合一).
性质:
应用格式:
,
三线合一
知识回顾
等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(简写成:三线合一).
性质:
应用格式:
,
三线合一
知识回顾
知识回顾
性质:等腰三角形的两个底角相等
(简写成:等边对等角).
情景:动脑思考
如图,位于海上两处的两艘救生船接到处遇险船只的报警,当时测得. 如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪的因素)?
情景:动脑思考
如图,位于海上两处的两艘救生船接到处遇险船只的报警,当时测得. 如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪的因素)?
探究:测一测
已知:如图,在△中,那么它们所对的边和有什么数量关系?
测量得到:.
过作平分交于点.
证法 ——作顶角平分线
在△和中,
,
,
,
.
.
过作交于,.
在△和中,
,
,
,
.
.
证法——作底边上的高
证法——作两腰的高
过作中线,则.
作,,垂足分别为,.
在△与中,
,
,
,
.
证法——作两腰的高
过作中线,则.
作,,垂足分别为,.
证法——作两腰的高
在△与中,
,
,
,
.
过作中线,则.
作,,垂足分别为,.
又,,
,
,
,
,
.
证法——作两腰的高
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角
对等边”).
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这个三角形是等腰三角形(简写成“等角
对等边”).
应用格式:
在中,
即为等腰三角形.
辨析
错,因为都不是在同一个三角形中.
例题
求证
如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知是△的外角,,∥.
求证: .
例题
求证
如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知是△的外角,,∥.
求证: .
例题
求证
如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知是△的外角,,∥.
求证: .
例题—证明
.
又,
.
.
两直线平行,同位角相等
两直线平行,内错角相等
等角对等边
例题—作图
已知等腰三角形底边长为,底边上的高的长为,求作这个等腰三角形.
点应该在底边的垂直平分线上.
例题—作图
作法:
.作线段.
.作线段的垂直平分线交点.
.在上取一点,使.
.连接和,则△即为所求.
课堂练习
已知:如图,∥,平分.
求证:.
课堂练习
已知:如图,∥,平分.
求证:.
课堂练习
已知:如图,∥,平分.
求证:.
课堂练习
已知:如图,∥,平分.
求证:.
证明:∥,
.
课堂练习
已知:如图,∥,平分.
求证:.
证明:∥,
.
平分,
课堂练习
已知:如图,∥,平分.
求证:.
证明:∥,
.
平分,
.
课
堂
小
结
知识内容
等腰三角形的判定:
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
课
堂
小
结
教学方法
判定线段之间的数量关系,一般做法是通过全等或利用“等角对等边”,运用转化思想,解决问题.
比较等腰三角形的性质和判定:
“等边对等角”与“等角对等边”,条件与结论是对调的,运用逆向思维观察和思考,可以提升自己的理性思维.
课后作业
三角形
三角形
三角形
三角形
一个三角形的一个外角为,且它恰好等于一个不相邻的内角的倍,这个三角形是( ).
1
课后作业
一个三角形的一个外角为,且它恰好等于一个不相邻的内角的倍,这个三角形是( ).
1
三角形
三角形
三角形
三角形
课后作业
如图,已知,则______,图中的等腰三角形有________.
2
课后作业
如图,已知,则______,图中的等腰三角形有________.
2
课后作业
已知:如图,,和相交于点.
求证:△是等腰三角形.
3
课后作业
如图,上午时,一条船从处出发以每小时海里的速度向正北航行,中午时到达处,从、望灯塔,测得,,求从处到灯塔的距离.
4
北
