人教版八年级数学上册12.3角的平分线的性质(3)教学课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.3角的平分线的性质(3)教学课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 20:40:26 | ||
图片预览



文档简介
(共19张PPT)
(第三课时)
角的平分线的性质
回顾
角的平分线的性质
角的平分线上的点到角的两边的距离相等.
题设
一个点在一个角的平分线上.
结论
它到角的两边的距离相等.
交换题设和结论,你能得到什么新命题 这个新命题正确吗
来看具体问题.
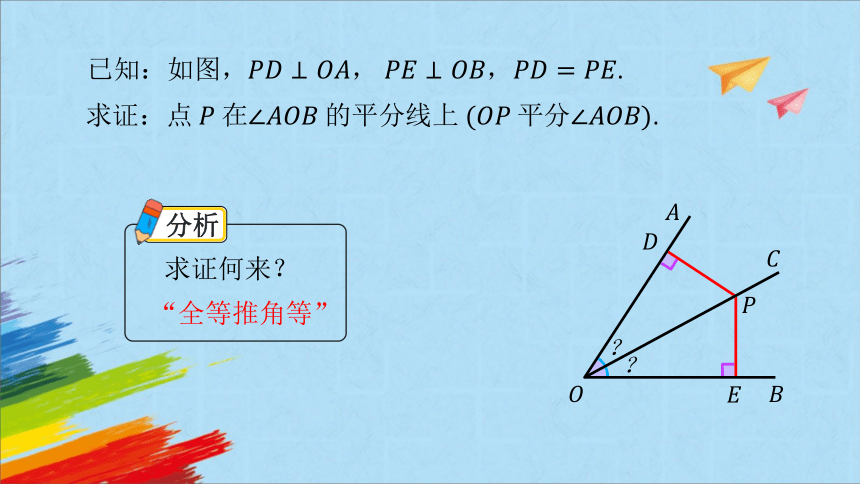
已知:如图,, ,.
求证:点分.
?
?
求证何来?
“全等推角等”
分析
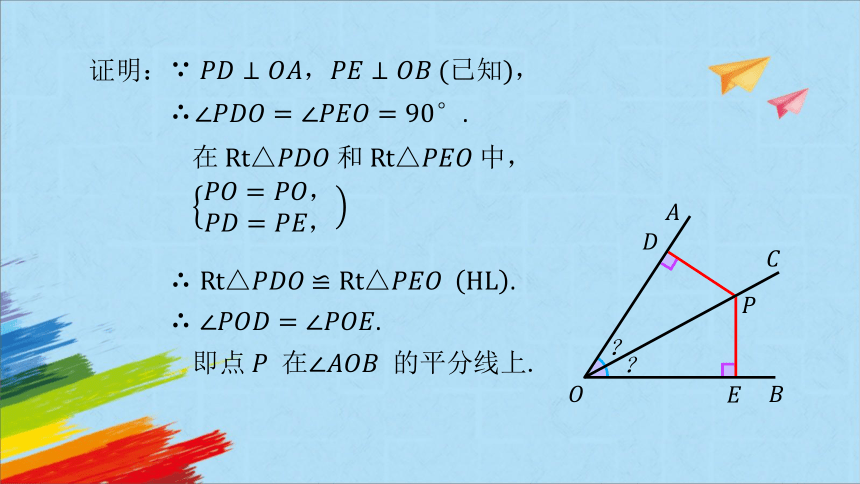
证明:
),
.
在△ △
△ △.
.
?
?
即点 在 的平分线上.
新的定理
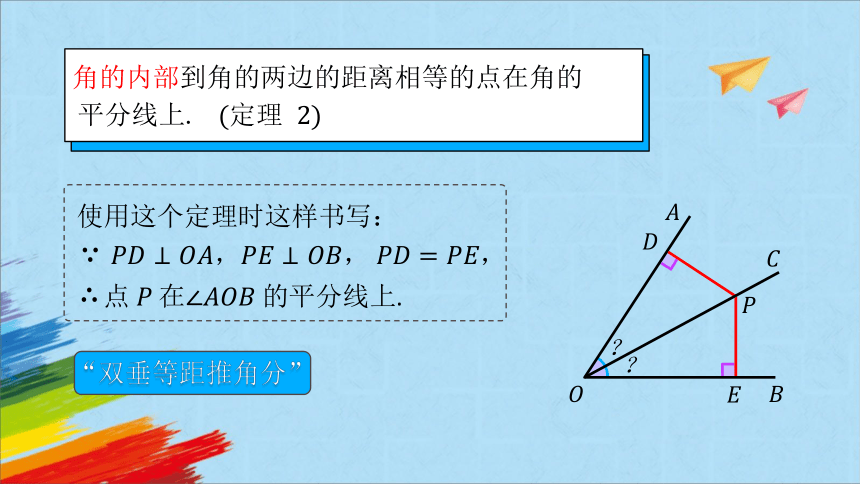
角的内部到角的两边的距离相等的点在角的
平分线上. 定理
留一个思考问题:
为什么会有“角的内部”这个前提
没有的话会怎样
角的内部到角的两边的距离相等的点在角的
平分线上. 定理
使用这个定理时这样书写:
,
点.
“双垂等距推角分”
?
?
?
?
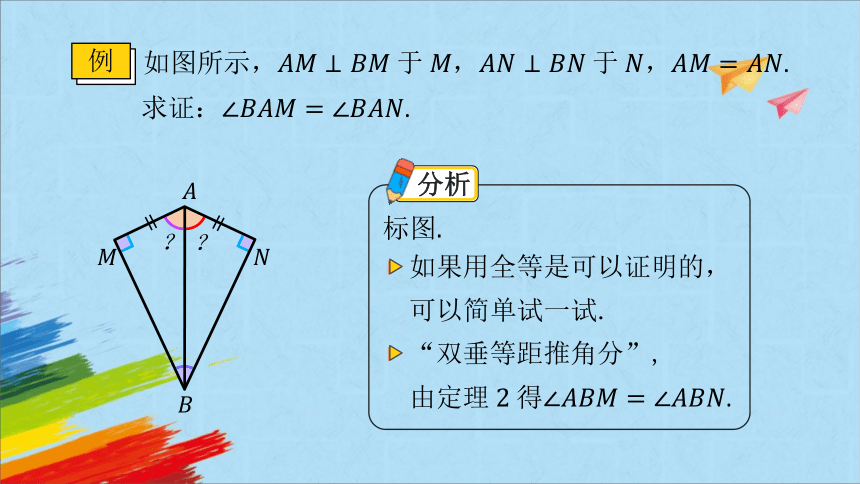
如图所示,,,.
例
求证:.
分析
如果用全等是可以证明的,
可以简单试一试.
“双垂等距推角分”,
由.
?
?
证明:
,
即.
(角的内部到角的两边的距离相等的点在角的平分线上. )
(等角的余角相等).
积累不同证明方法.
?
如图,在且 于 , 于 . 求
度数.
例
分析
已知可推?
“双垂等距推角分”,
可得平分.
再由得,
最后在求角.
?
解:
.
于 , 于
.
.
.
基本图不变
如图,,,,
例
求证:.
分析
已知可推?
△ △.
求证何来
全等?定理更好.
需要 .
1
2
证明:
,
在△ △
.
,
.
又
上,
即.
?
?
如图,,, 分别是△ 的三条边上的点,,△和△的面积相等.
例
求证: 平分.
分析
已知可推?
直接用面积要找底高,
面积和一边等,则高等.
考虑作垂直,
求证何来
“双垂等距推角分”.
1
2
,△和△的面积相等.
例
求证: 平分.
证明:
过 作 于 , 于 .
△ △面积相等,
.
又
.
又
?
?
辅助线不变
如图, 为 内一条射线,, 分别为, 上两点,且 .
例
分析
已知可推?
邻补角好找.
求证何来
可以转换为等角的条件.
求证: 平分.
?
?
“双垂等距推角分”.
作双垂,欠等距,
全等推.
1
2
则.
过点 作 于 , 于.
证明:
.
在△ △
,
?
?
又
课
堂
小
结
角的内部到角的两边的距离相等的点在角的平分线上.
新的定理
“双垂等距推角分”.
新的应用
两个定理的异同(基本图,辅助线相同).
新的关注
课后作业
C. 三角形三条角平分线的交点到三条边的距离相等
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
D. 以上均不正确
求证:.
△
课后作业
(第三课时)
角的平分线的性质
回顾
角的平分线的性质
角的平分线上的点到角的两边的距离相等.
题设
一个点在一个角的平分线上.
结论
它到角的两边的距离相等.
交换题设和结论,你能得到什么新命题 这个新命题正确吗
来看具体问题.
已知:如图,, ,.
求证:点分.
?
?
求证何来?
“全等推角等”
分析
证明:
),
.
在△ △
△ △.
.
?
?
即点 在 的平分线上.
新的定理
角的内部到角的两边的距离相等的点在角的
平分线上. 定理
留一个思考问题:
为什么会有“角的内部”这个前提
没有的话会怎样
角的内部到角的两边的距离相等的点在角的
平分线上. 定理
使用这个定理时这样书写:
,
点.
“双垂等距推角分”
?
?
?
?
如图所示,,,.
例
求证:.
分析
如果用全等是可以证明的,
可以简单试一试.
“双垂等距推角分”,
由.
?
?
证明:
,
即.
(角的内部到角的两边的距离相等的点在角的平分线上. )
(等角的余角相等).
积累不同证明方法.
?
如图,在且 于 , 于 . 求
度数.
例
分析
已知可推?
“双垂等距推角分”,
可得平分.
再由得,
最后在求角.
?
解:
.
于 , 于
.
.
.
基本图不变
如图,,,,
例
求证:.
分析
已知可推?
△ △.
求证何来
全等?定理更好.
需要 .
1
2
证明:
,
在△ △
.
,
.
又
上,
即.
?
?
如图,,, 分别是△ 的三条边上的点,,△和△的面积相等.
例
求证: 平分.
分析
已知可推?
直接用面积要找底高,
面积和一边等,则高等.
考虑作垂直,
求证何来
“双垂等距推角分”.
1
2
,△和△的面积相等.
例
求证: 平分.
证明:
过 作 于 , 于 .
△ △面积相等,
.
又
.
又
?
?
辅助线不变
如图, 为 内一条射线,, 分别为, 上两点,且 .
例
分析
已知可推?
邻补角好找.
求证何来
可以转换为等角的条件.
求证: 平分.
?
?
“双垂等距推角分”.
作双垂,欠等距,
全等推.
1
2
则.
过点 作 于 , 于.
证明:
.
在△ △
,
?
?
又
课
堂
小
结
角的内部到角的两边的距离相等的点在角的平分线上.
新的定理
“双垂等距推角分”.
新的应用
两个定理的异同(基本图,辅助线相同).
新的关注
课后作业
C. 三角形三条角平分线的交点到三条边的距离相等
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
D. 以上均不正确
求证:.
△
课后作业
