人教版八年级数学上册12.3角的平分线的性质(1)教学课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.3角的平分线的性质(1)教学课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 20:41:21 | ||
图片预览




文档简介
(共20张PPT)
(第一课时)
角的平分线的性质
画一个角(如图),怎样得到这个角的平分线
学习与探究
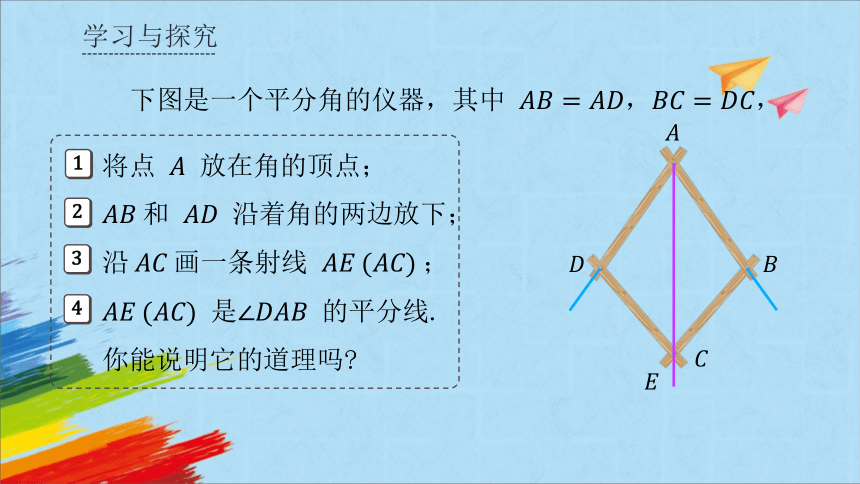
下图是一个平分角的仪器,其中
你能说明它的道理吗
将点 放在角的顶点;
1
和 沿着角的两边放下;
2
沿画一条射线 ;
3
是 的平分线.
4
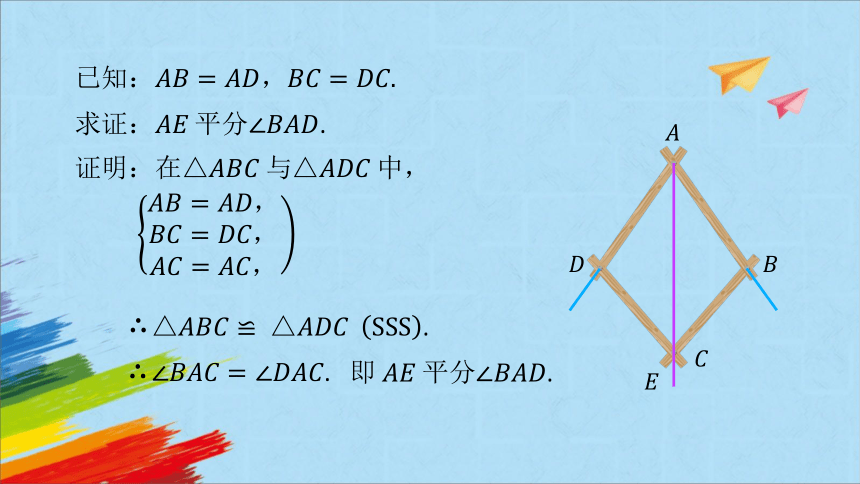
已知:
求证:.
证明:△△
△△.
.
即.
利用尺规作角的平分线:
已知:(如图).
求作: 的平分线.
作法
1
以为圆心,适当长为半径作弧,
交 于 ,交 于;
2
大于 的长为半径作弧,
分别以, 为圆心,
两弧在内部交于点;
3
作射线.
则射线即为所求.
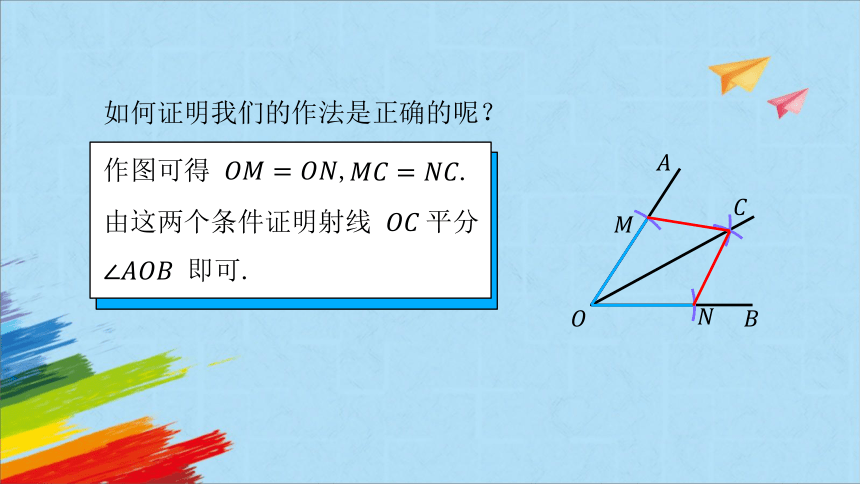
如何证明我们的作法是正确的呢?
作图可得 ,
由这两个条件证明射线 平分 即可.
.
证明:连接 ,.
据作图可得,.
则在△和△ 中,
△△.
即射线.
利用尺规我们可以作一个角的平分线,那么角的平分线有什么性质呢
思考
操作
请同学们把一个角沿角平分线折叠,任意剪一刀后再展开,有什么发现
猜想
如图,点 在 上,,,垂足分别为点 ,.
猜想线段与的大小关系:
证明
角平分线上的点到角的两边的距离相等.
题设:一个点在一个角的平分线上.
结论:它到角的两边的距离相等.
已知:如图,点 在 上,,,垂足分别为点 ,.
求证:.
由△△
分析
证明:
在△和△ 中,
,
,,
.
△△.
.
阅读教材
一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即
1
明确命题中的已知和求证;
2
根据题意,画出图形,并用数学符号表示已知和求证;
3
经过分析,找出由已知推出要证的结论的途径,写出证明过程.
角的平分线的性质:
角的平分线上的点到角的两边的距离相等.
使用定理时这样书写:
于 ,,
,
.
分析
.
1
求证何来?
由“距离” 想作垂直.
2
已知可推?
由“角分双垂”想到角的平分线的性质.
如图,点 是平分线上一点,于 ,,求点到边 的距离.
例
解:过 作 于点.
如图,点 是平分线上一点,于 ,,求点到边 的距离.
例
点 是 平分线上一点, 于
.
.
.
课
堂
小
结
尺规作图作一个角的角平分线.
尺规作图
角平分线上的点到角的两边的距离相等.
角平分线的性质定理
“角分双垂推等距”.
定理应用
课后作业
(第一课时)
角的平分线的性质
画一个角(如图),怎样得到这个角的平分线
学习与探究
下图是一个平分角的仪器,其中
你能说明它的道理吗
将点 放在角的顶点;
1
和 沿着角的两边放下;
2
沿画一条射线 ;
3
是 的平分线.
4
已知:
求证:.
证明:△△
△△.
.
即.
利用尺规作角的平分线:
已知:(如图).
求作: 的平分线.
作法
1
以为圆心,适当长为半径作弧,
交 于 ,交 于;
2
大于 的长为半径作弧,
分别以, 为圆心,
两弧在内部交于点;
3
作射线.
则射线即为所求.
如何证明我们的作法是正确的呢?
作图可得 ,
由这两个条件证明射线 平分 即可.
.
证明:连接 ,.
据作图可得,.
则在△和△ 中,
△△.
即射线.
利用尺规我们可以作一个角的平分线,那么角的平分线有什么性质呢
思考
操作
请同学们把一个角沿角平分线折叠,任意剪一刀后再展开,有什么发现
猜想
如图,点 在 上,,,垂足分别为点 ,.
猜想线段与的大小关系:
证明
角平分线上的点到角的两边的距离相等.
题设:一个点在一个角的平分线上.
结论:它到角的两边的距离相等.
已知:如图,点 在 上,,,垂足分别为点 ,.
求证:.
由△△
分析
证明:
在△和△ 中,
,
,,
.
△△.
.
阅读教材
一般情况下,我们要证明一个几何命题时,可以按照类似的步骤进行,即
1
明确命题中的已知和求证;
2
根据题意,画出图形,并用数学符号表示已知和求证;
3
经过分析,找出由已知推出要证的结论的途径,写出证明过程.
角的平分线的性质:
角的平分线上的点到角的两边的距离相等.
使用定理时这样书写:
于 ,,
,
.
分析
.
1
求证何来?
由“距离” 想作垂直.
2
已知可推?
由“角分双垂”想到角的平分线的性质.
如图,点 是平分线上一点,于 ,,求点到边 的距离.
例
解:过 作 于点.
如图,点 是平分线上一点,于 ,,求点到边 的距离.
例
点 是 平分线上一点, 于
.
.
.
课
堂
小
结
尺规作图作一个角的角平分线.
尺规作图
角平分线上的点到角的两边的距离相等.
角平分线的性质定理
“角分双垂推等距”.
定理应用
课后作业
