人教版八年级上册11.2.2 三角形的外角课件(共27张PPT)
文档属性
| 名称 | 人教版八年级上册11.2.2 三角形的外角课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 20:40:20 | ||
图片预览



文档简介
(共27张PPT)
三角形的外角
直角三角形的两个锐角互余.
分析
复习引入
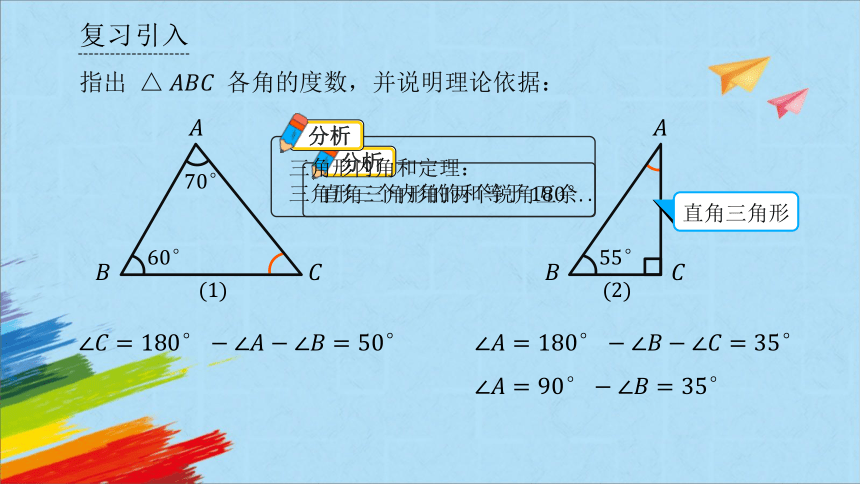
指出 各角的度数,并说明理论依据:
三角形内角和定理:
三角形三个内角的和等于 .
分析
直角三角形
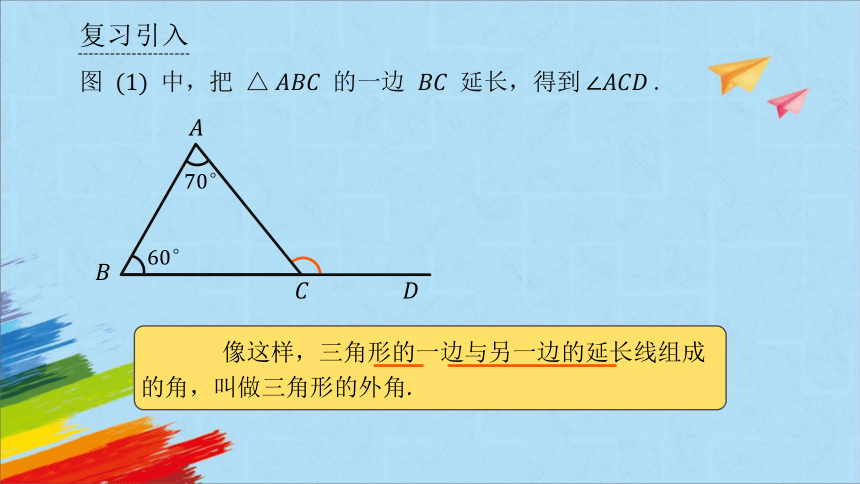
像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
图 中,把 的一边 延长,得到.
复习引入
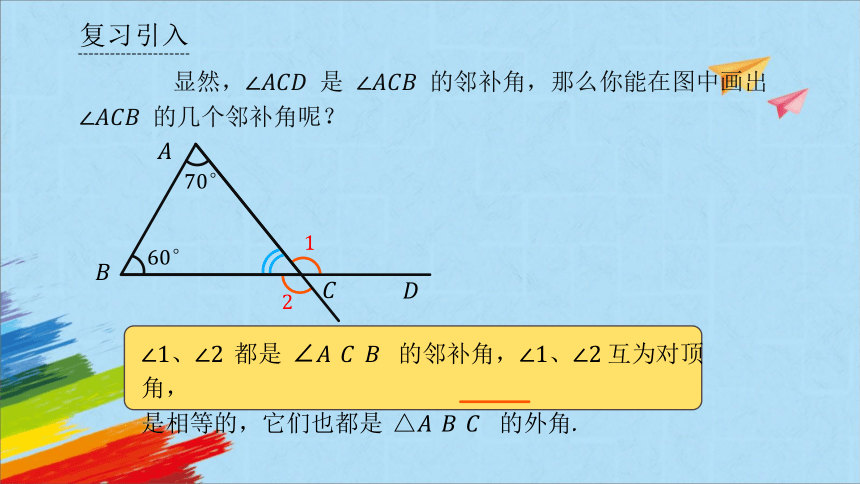
显然, 是 的邻补角,那么你能在图中画出 的几个邻补角呢?
复习引入
、 都是 ∠ 的邻补角,、互为对顶角,
是相等的,它们也都是 △ 的外角.
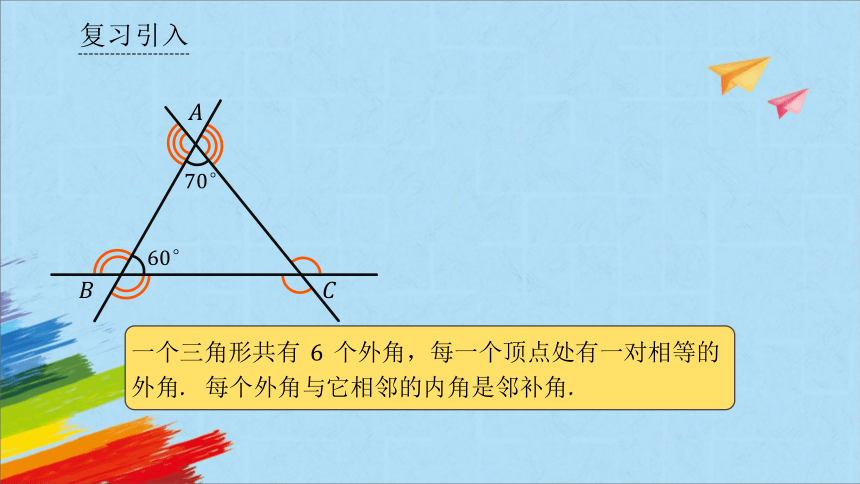
一个三角形共有 个外角,每一个顶点处有一对相等的外角. 每个外角与它相邻的内角是邻补角.
复习引入
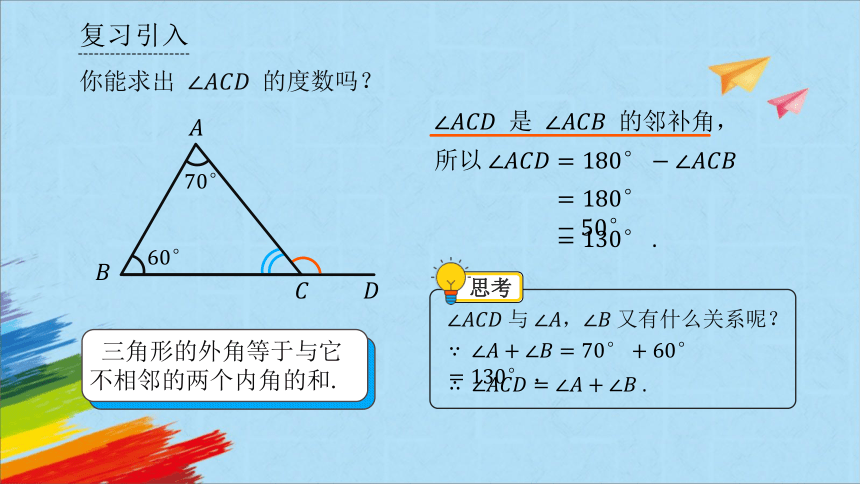
三角形的外角等于与它不相邻的两个内角的和.
你能求出 的度数吗?
是 的邻补角,
所以
.
.
与 , 又有什么关系呢?
思考
复习引入
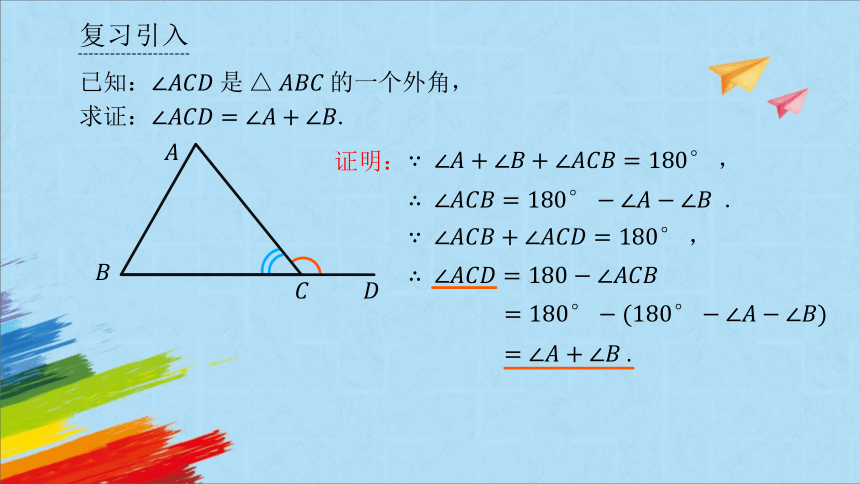
已知: 是 的一个外角,
求证: .
任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
复习引入
已知: 是 的一个外角,
求证:.
.
.
证明:
复习引入
三角形的外角等于与它不相邻的两个内角的和.
一般地,由三角形内角和定理可以推出下面的推论:
推论是由定理直接推出的结论. 和定理一样,推论可以作为进一步推理的依据.
复习引入
三角形的外角等于与它不相邻的两个内角的和.
是 的一个外角,
.
符号语言
复习引入
如图,口答.
;
.
练习
分析
是 的内角,
三角形的外角等于与它不相邻的两个内角的和.
.
.
是 的一个外角,
1
2
练习
分析
是 的一个外角,
三角形的外角等于与它不相邻的两个内角的和.
1
2
如图,口答.
;
.
.
练习
说出图中 的度数.
三角形的外角等于与它不相邻的两个内角的和.
分析
练习
说出图中 的度数.
例题
例
如图, 是 的三个外角,它们的和是多少?
,
.
三角形的外角等于与它不相邻的两个内角的和.
分析
解:
,
你还有其他解法吗?
思考
例题
例
如图, 是 的三个外角,它们的和是多少?
由 ,
由 ,
,
得
得 .
,
得
解:
三角形的外角等于与它相邻的内角的补角.
分析
三角形的外角和等于
三角形的每个顶点处有两个外角,它们相等,所以每个顶点处只取一个外角,把它们的和叫做三角形的外角和.
例题
例
如图, 是同一条直线上的四个点, , ,你能求出 的度数吗?
分析
是 的外角,
所以 ,
而 ,
由此可求.
例题
,
,
.
是 的外角,
解:
例
如图, 是同一条直线上的四个点, , ,你能求出 的度数吗?
如图, 是同一条直线上的四个点, , ,你能求出 的度数吗?
例题
分析
也是 的外角,
例
所以 ,
由此可求.
而 也是 的外角,
所以,
例题
是 的外角,
,
是 外角,
解:
例
如图, 是同一条直线上的四个点, , ,你能求出 的度数吗?
练习
分析
都是 的内角,
如图, 是 的 边上一点, , , ,求 的度数; 的度数.
已知 ,
但不知道
在 中不能解决问题.
练习
分析
,
是 的外角,
如图, 是 的 边上一点, , , ,求 的度数; 的度数.
即,
而
由此可以求出 的度数,
进而利用三角形内角和定理,可求出 的度数.
是 的外角,
,
,
,
.
解:
练习
如图, 是 的 边上一点, , , ,求 的度数; 的度数.
三角形的外角的定义:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
本节课学习的内容:
三角形外角定理:
三角形的外角等于与它不相邻的两个内角的和.
三角形的外角和等于 .
每一个顶点处只取一个外角,三个外角之和等于 .
注意
课
堂
小
结
怎样探索并证明“三角形的外角等于与它不相邻的两个内角的和”?
三角形外角和定理
三角形内角和定理
课
堂
小
结
推论是由定理直接推出的结论. 和定理一样,推论可以作为进一步推理的依据.
作业
如图,∥, , ,求 和 的度数.
5
教科书 页 习题
如图,∥, , ,求 的度数.
6
三角形的外角
直角三角形的两个锐角互余.
分析
复习引入
指出 各角的度数,并说明理论依据:
三角形内角和定理:
三角形三个内角的和等于 .
分析
直角三角形
像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
图 中,把 的一边 延长,得到.
复习引入
显然, 是 的邻补角,那么你能在图中画出 的几个邻补角呢?
复习引入
、 都是 ∠ 的邻补角,、互为对顶角,
是相等的,它们也都是 △ 的外角.
一个三角形共有 个外角,每一个顶点处有一对相等的外角. 每个外角与它相邻的内角是邻补角.
复习引入
三角形的外角等于与它不相邻的两个内角的和.
你能求出 的度数吗?
是 的邻补角,
所以
.
.
与 , 又有什么关系呢?
思考
复习引入
已知: 是 的一个外角,
求证: .
任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
复习引入
已知: 是 的一个外角,
求证:.
.
.
证明:
复习引入
三角形的外角等于与它不相邻的两个内角的和.
一般地,由三角形内角和定理可以推出下面的推论:
推论是由定理直接推出的结论. 和定理一样,推论可以作为进一步推理的依据.
复习引入
三角形的外角等于与它不相邻的两个内角的和.
是 的一个外角,
.
符号语言
复习引入
如图,口答.
;
.
练习
分析
是 的内角,
三角形的外角等于与它不相邻的两个内角的和.
.
.
是 的一个外角,
1
2
练习
分析
是 的一个外角,
三角形的外角等于与它不相邻的两个内角的和.
1
2
如图,口答.
;
.
.
练习
说出图中 的度数.
三角形的外角等于与它不相邻的两个内角的和.
分析
练习
说出图中 的度数.
例题
例
如图, 是 的三个外角,它们的和是多少?
,
.
三角形的外角等于与它不相邻的两个内角的和.
分析
解:
,
你还有其他解法吗?
思考
例题
例
如图, 是 的三个外角,它们的和是多少?
由 ,
由 ,
,
得
得 .
,
得
解:
三角形的外角等于与它相邻的内角的补角.
分析
三角形的外角和等于
三角形的每个顶点处有两个外角,它们相等,所以每个顶点处只取一个外角,把它们的和叫做三角形的外角和.
例题
例
如图, 是同一条直线上的四个点, , ,你能求出 的度数吗?
分析
是 的外角,
所以 ,
而 ,
由此可求.
例题
,
,
.
是 的外角,
解:
例
如图, 是同一条直线上的四个点, , ,你能求出 的度数吗?
如图, 是同一条直线上的四个点, , ,你能求出 的度数吗?
例题
分析
也是 的外角,
例
所以 ,
由此可求.
而 也是 的外角,
所以,
例题
是 的外角,
,
是 外角,
解:
例
如图, 是同一条直线上的四个点, , ,你能求出 的度数吗?
练习
分析
都是 的内角,
如图, 是 的 边上一点, , , ,求 的度数; 的度数.
已知 ,
但不知道
在 中不能解决问题.
练习
分析
,
是 的外角,
如图, 是 的 边上一点, , , ,求 的度数; 的度数.
即,
而
由此可以求出 的度数,
进而利用三角形内角和定理,可求出 的度数.
是 的外角,
,
,
,
.
解:
练习
如图, 是 的 边上一点, , , ,求 的度数; 的度数.
三角形的外角的定义:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
本节课学习的内容:
三角形外角定理:
三角形的外角等于与它不相邻的两个内角的和.
三角形的外角和等于 .
每一个顶点处只取一个外角,三个外角之和等于 .
注意
课
堂
小
结
怎样探索并证明“三角形的外角等于与它不相邻的两个内角的和”?
三角形外角和定理
三角形内角和定理
课
堂
小
结
推论是由定理直接推出的结论. 和定理一样,推论可以作为进一步推理的依据.
作业
如图,∥, , ,求 和 的度数.
5
教科书 页 习题
如图,∥, , ,求 的度数.
6
