人教版八年级数学上册《同底数幂的乘法》 课件(共46张PPT)
文档属性
| 名称 | 人教版八年级数学上册《同底数幂的乘法》 课件(共46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 00:00:00 | ||
图片预览







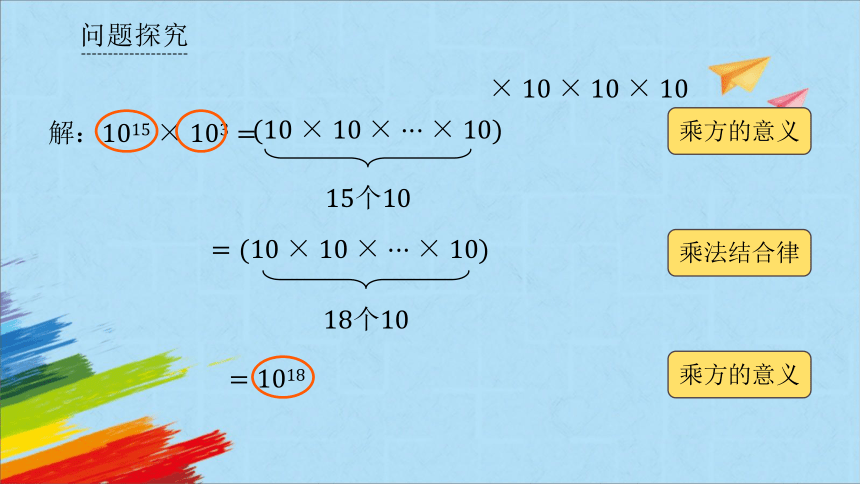

文档简介
(共46张PPT)
同底数幂的乘法
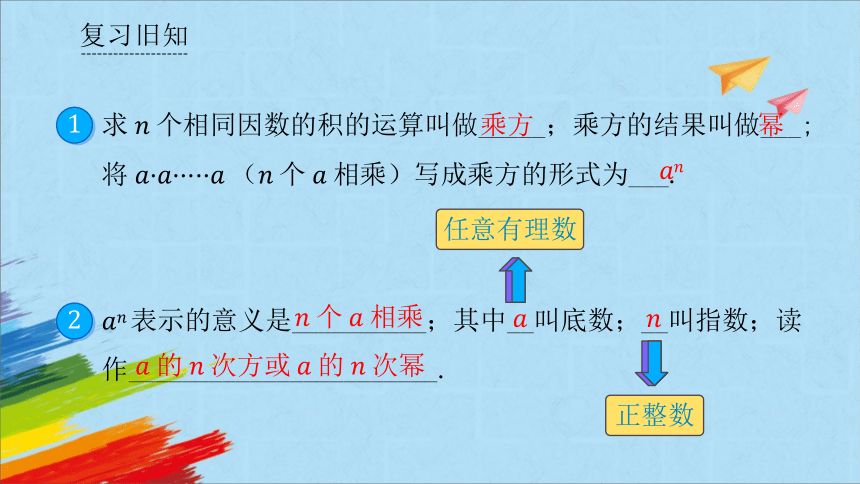
求个相同因数的积的运算叫做_____;乘方的结果叫做___;将个相乘写成乘方的形式为___.
表示的意义是__________;其中__叫底数;__叫指数;读作_______________________.
复习旧知
1
2
乘方
幂
个相乘
的次方或的次幂
任意有理数
正整数
把下列各式写成乘方的形式.
复习旧知
3
________________;
1
2
3
4
________________;
_______________;
________________.
个
___;
把下列各式写成乘方的形式.
复习旧知
3
___;
底数为,指数是
底数为,指数是
1
2
______;
___.
个
把下列各式写成乘方的形式.
复习旧知
3
底数为,指数是
底数为,指数是
3
4
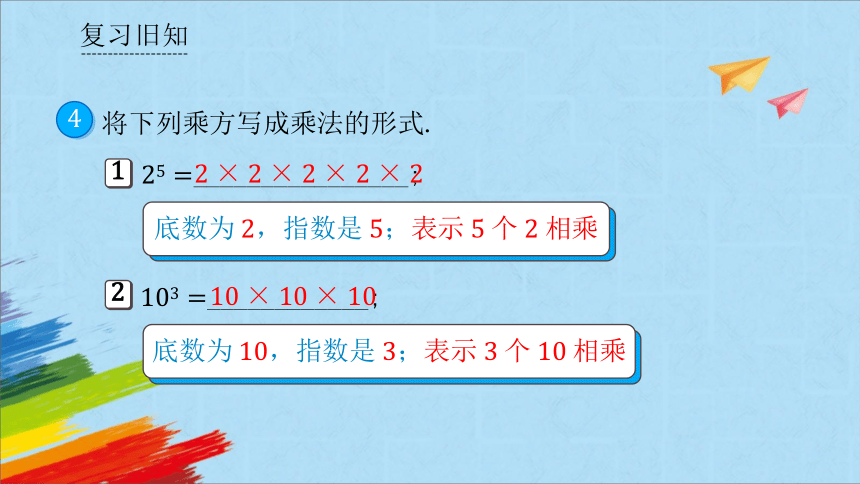
将下列乘方写成乘法的形式.
复习旧知
4
_________________;
1
2
3
4
________________;
_________________;
_________________.
________________;
将下列乘方写成乘法的形式.
复习旧知
4
____________;
底数为,指数是表示个相乘
底数为,指数是表示个相乘
1
2
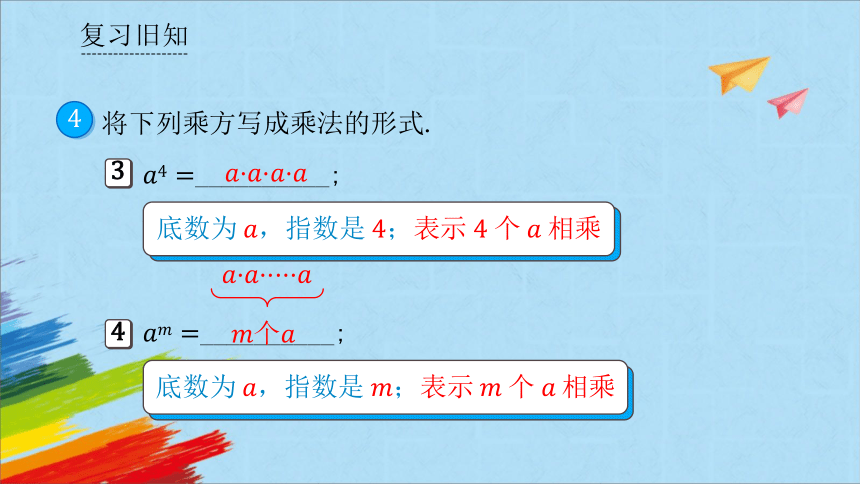
将下列乘方写成乘法的形式.
复习旧知
4
__________;
__________;
底数为,指数是表示个相乘
底数为,指数是表示个相乘
3
4
在年月的全球超级计算机排行榜中,中国的神威·太湖之光超级计算机位居全球第三.
已知一种电子计算机每秒可进行千万亿次运算,它工作可进行多少次运算呢?
问题探究
在年月的全球超级计算机排行榜中,中国的神威·太湖之光超级计算机位居全球第三.
已知一种电子计算机每秒可进行千万亿次运算,它工作可进行多少次运算呢?
问题探究
解:
问题探究
乘方的意义
乘法结合律
乘方的意义
探究新知
2
3
都是正整数
1
根据乘方的意义填空,观察计算结果你能发现什么规律?
根据乘方的意义填空,观察计算结果你能发现什么规律?
1
探究新知
2
根据乘方的意义填空,观察计算结果你能发现什么规律?
探究新知
3
个
根据乘方的意义填空,观察计算结果你能发现什么规律?
探究新知
1
2
3
都是正整数
根据乘方的意义填空,观察计算结果你能发现什么规律?
探究新知
上述三个乘法运算的乘数有什么共同的特征吗?
思考
乘数均为同底数的幂
探究新知
你能再举一个例子,使它具有上述三个乘法运算的乘数的共同特征,不写计算过程直接说出它的运算结果.
思考
探究新知
你能用符号表示你发现的规律吗?
思考
都是正整数
探究新知
你能用符号表示你发现的规律吗?
思考
探究新知
都是正整数
你能将上述发现的规律推导出来吗?
乘方的意义
乘法结合律
个
乘方的意义
探究新知
你能将上述发现的规律推导出来吗?
乘方的意义
乘法结合律
个
乘方的意义
探究新知
通过上面的探索和推导,你能用文字语言概括出同底数幂的乘法的运算性质吗?
同底数幂相乘,
探究新知
底数不变,
指数相加.
都是正整数表述了两个同底数幂相乘的结果,那么,三个、四个······多个同底数幂相乘,结果会怎样
思考
探究新知
三个同底数幂相乘,结果会怎样?
都是正整数
解法一
探究新知
三个同底数幂相乘,结果会怎样?
底数不变,指数相加.
探究新知
解法二
都是正整数
多个同底数幂相乘,结果会怎样?
都是正整数
探究新知
例题讲解
例
1
2
3
4
例题讲解
1
2
例
例题讲解
3
4
例
例题讲解
3
4
注意:单个字母或者数字的指数为.
例
练习巩固
下列计算是否正确,并简要说明理由.
1
2
3
4
练习
5
练习巩固
1
2
练习
注意:当底数为多项式时,将此多项式看作一个整体进行计算.
例题讲解
已知.
1
例
逆用
例题讲解
如果.
2
例
例题讲解
如果.
2
例
例题讲解
如果.
2
例
例题讲解
.
3
例
转化为同底数幂
例题讲解
1
例
2
3
练习巩固
1
练习
2
练习巩固
1
练习
2
练习巩固
1
练习
2
练习巩固
1
练习
2
课
堂
小
结
同底数幂的乘法运算性质
同底数幂相乘,底数不变,指数相加.
都是正整数
课
堂
小
结
特殊
具体
一般
抽象
;
课后作业
填空:
;
1
1
3
;
5
;
2
;
4
.
6
解答:
2
.
1
若.
2
选做:
;
1
.
2
同底数幂的乘法
求个相同因数的积的运算叫做_____;乘方的结果叫做___;将个相乘写成乘方的形式为___.
表示的意义是__________;其中__叫底数;__叫指数;读作_______________________.
复习旧知
1
2
乘方
幂
个相乘
的次方或的次幂
任意有理数
正整数
把下列各式写成乘方的形式.
复习旧知
3
________________;
1
2
3
4
________________;
_______________;
________________.
个
___;
把下列各式写成乘方的形式.
复习旧知
3
___;
底数为,指数是
底数为,指数是
1
2
______;
___.
个
把下列各式写成乘方的形式.
复习旧知
3
底数为,指数是
底数为,指数是
3
4
将下列乘方写成乘法的形式.
复习旧知
4
_________________;
1
2
3
4
________________;
_________________;
_________________.
________________;
将下列乘方写成乘法的形式.
复习旧知
4
____________;
底数为,指数是表示个相乘
底数为,指数是表示个相乘
1
2
将下列乘方写成乘法的形式.
复习旧知
4
__________;
__________;
底数为,指数是表示个相乘
底数为,指数是表示个相乘
3
4
在年月的全球超级计算机排行榜中,中国的神威·太湖之光超级计算机位居全球第三.
已知一种电子计算机每秒可进行千万亿次运算,它工作可进行多少次运算呢?
问题探究
在年月的全球超级计算机排行榜中,中国的神威·太湖之光超级计算机位居全球第三.
已知一种电子计算机每秒可进行千万亿次运算,它工作可进行多少次运算呢?
问题探究
解:
问题探究
乘方的意义
乘法结合律
乘方的意义
探究新知
2
3
都是正整数
1
根据乘方的意义填空,观察计算结果你能发现什么规律?
根据乘方的意义填空,观察计算结果你能发现什么规律?
1
探究新知
2
根据乘方的意义填空,观察计算结果你能发现什么规律?
探究新知
3
个
根据乘方的意义填空,观察计算结果你能发现什么规律?
探究新知
1
2
3
都是正整数
根据乘方的意义填空,观察计算结果你能发现什么规律?
探究新知
上述三个乘法运算的乘数有什么共同的特征吗?
思考
乘数均为同底数的幂
探究新知
你能再举一个例子,使它具有上述三个乘法运算的乘数的共同特征,不写计算过程直接说出它的运算结果.
思考
探究新知
你能用符号表示你发现的规律吗?
思考
都是正整数
探究新知
你能用符号表示你发现的规律吗?
思考
探究新知
都是正整数
你能将上述发现的规律推导出来吗?
乘方的意义
乘法结合律
个
乘方的意义
探究新知
你能将上述发现的规律推导出来吗?
乘方的意义
乘法结合律
个
乘方的意义
探究新知
通过上面的探索和推导,你能用文字语言概括出同底数幂的乘法的运算性质吗?
同底数幂相乘,
探究新知
底数不变,
指数相加.
都是正整数表述了两个同底数幂相乘的结果,那么,三个、四个······多个同底数幂相乘,结果会怎样
思考
探究新知
三个同底数幂相乘,结果会怎样?
都是正整数
解法一
探究新知
三个同底数幂相乘,结果会怎样?
底数不变,指数相加.
探究新知
解法二
都是正整数
多个同底数幂相乘,结果会怎样?
都是正整数
探究新知
例题讲解
例
1
2
3
4
例题讲解
1
2
例
例题讲解
3
4
例
例题讲解
3
4
注意:单个字母或者数字的指数为.
例
练习巩固
下列计算是否正确,并简要说明理由.
1
2
3
4
练习
5
练习巩固
1
2
练习
注意:当底数为多项式时,将此多项式看作一个整体进行计算.
例题讲解
已知.
1
例
逆用
例题讲解
如果.
2
例
例题讲解
如果.
2
例
例题讲解
如果.
2
例
例题讲解
.
3
例
转化为同底数幂
例题讲解
1
例
2
3
练习巩固
1
练习
2
练习巩固
1
练习
2
练习巩固
1
练习
2
练习巩固
1
练习
2
课
堂
小
结
同底数幂的乘法运算性质
同底数幂相乘,底数不变,指数相加.
都是正整数
课
堂
小
结
特殊
具体
一般
抽象
;
课后作业
填空:
;
1
1
3
;
5
;
2
;
4
.
6
解答:
2
.
1
若.
2
选做:
;
1
.
2
