人教版八年级数学上册《三角形全等的判定-SSS》 课件(共38张PPT)
文档属性
| 名称 | 人教版八年级数学上册《三角形全等的判定-SSS》 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-18 21:32:24 | ||
图片预览



文档简介
(共38张PPT)
三角形全等的判定-
形状、大小相同的图形放在一起能够完全重合,能够完全重合的两个图形叫做全等形.
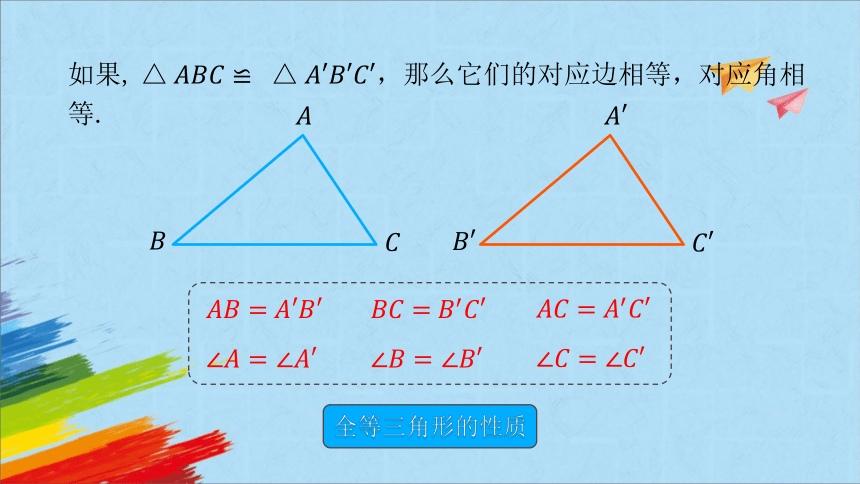
如果, 那么它们的对应边相等,对应角相等.
全等三角形的性质
就能判定
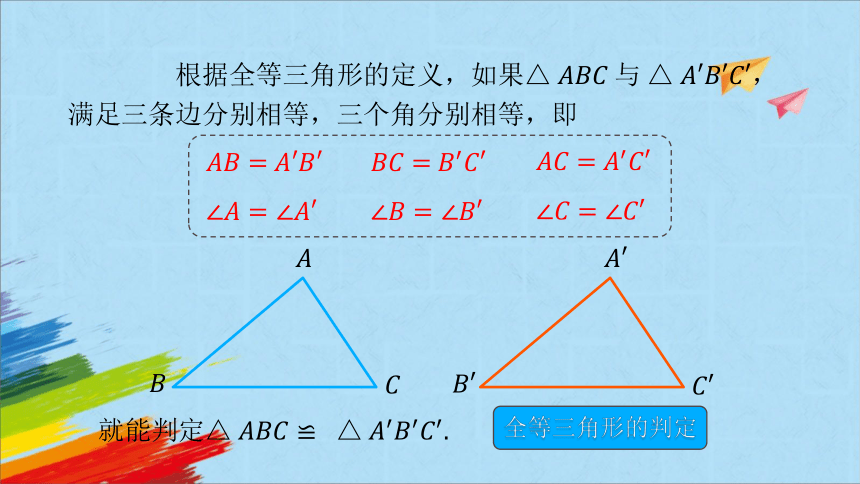
全等三角形的判定
根据全等三角形的定义,如果满足三条边分别相等,三个角分别相等,即
对两个三角形来说,以下六个条件中至少要满足几个条件,才能确保两个三角形全等呢
思考
关于边的条件
关于角的条件
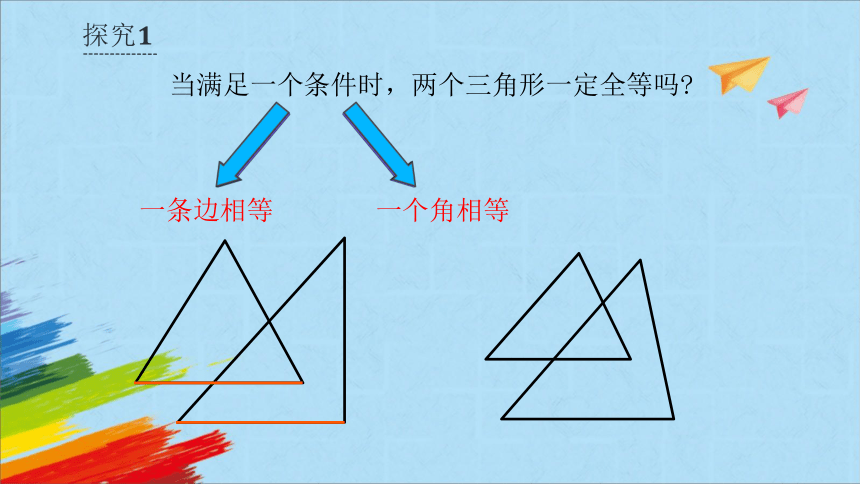
当满足一个条件时,两个三角形一定全等吗
探究
一条边相等
一个角相等
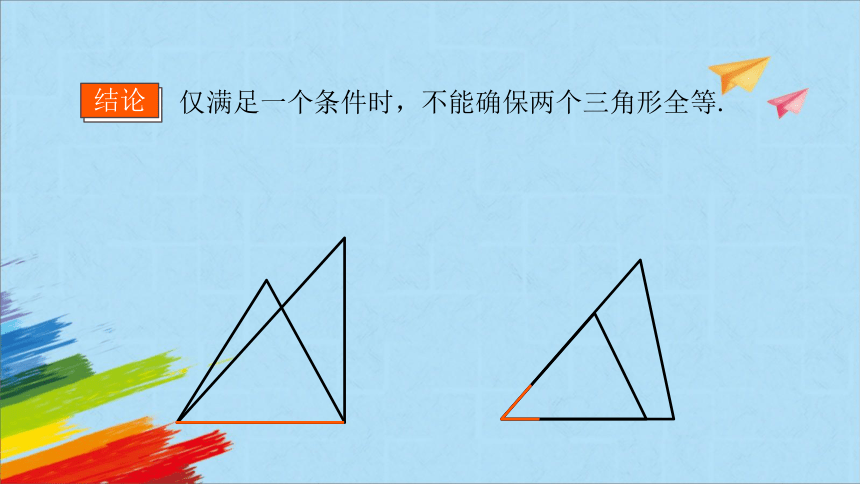
仅满足一个条件时,不能确保两个三角形全等.
结论
探究
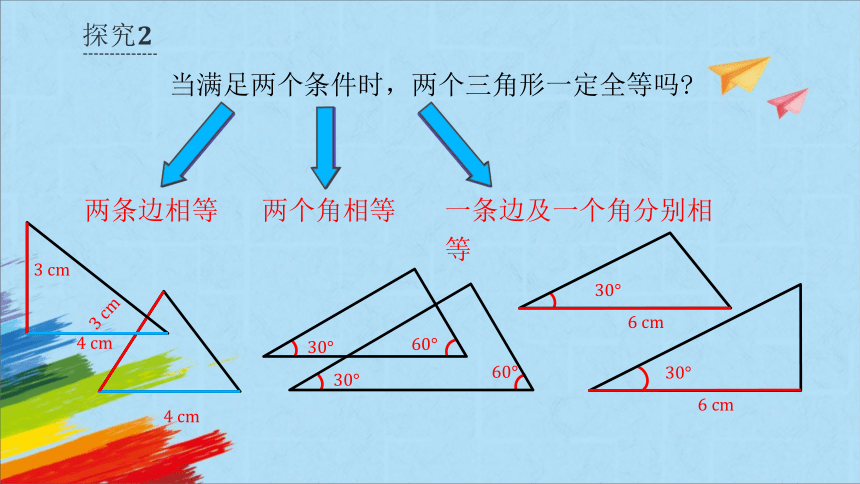
当满足两个条件时,两个三角形一定全等吗
两条边相等
一条边及一个角分别相等
两个角相等
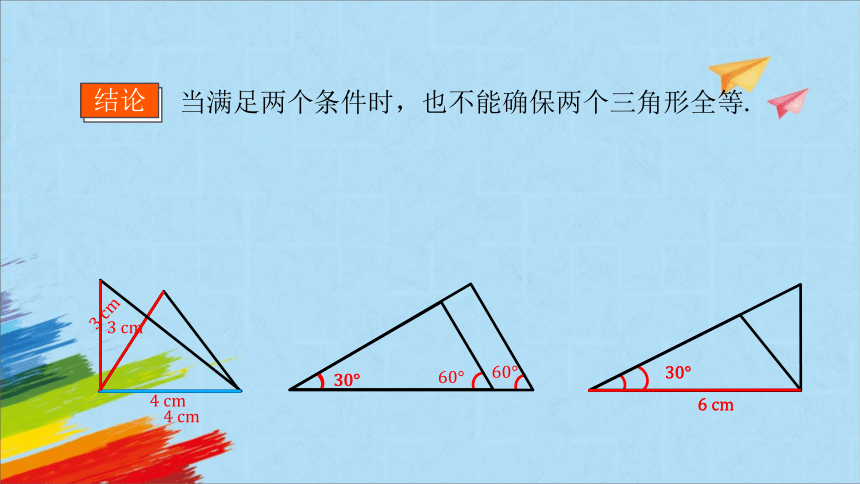
当满足两个条件时,也不能确保两个三角形全等.
结论
探究
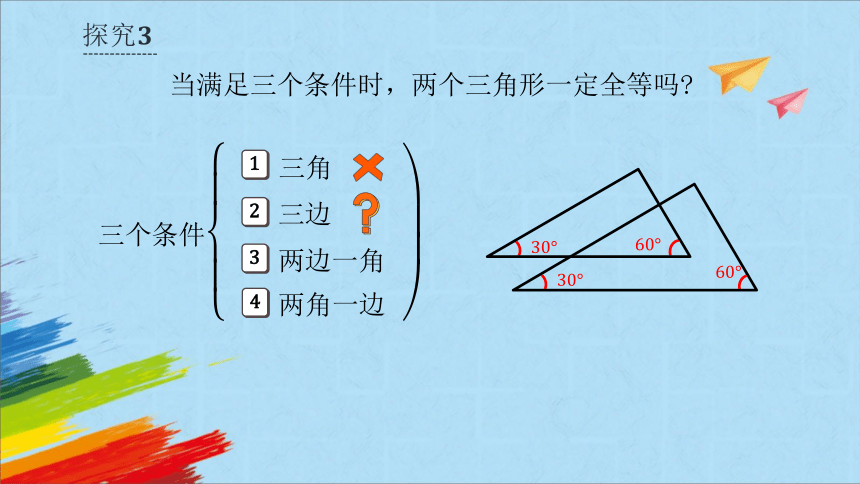
当满足三个条件时,两个三角形一定全等吗
三个条件
1
2
3
一角
4
一边
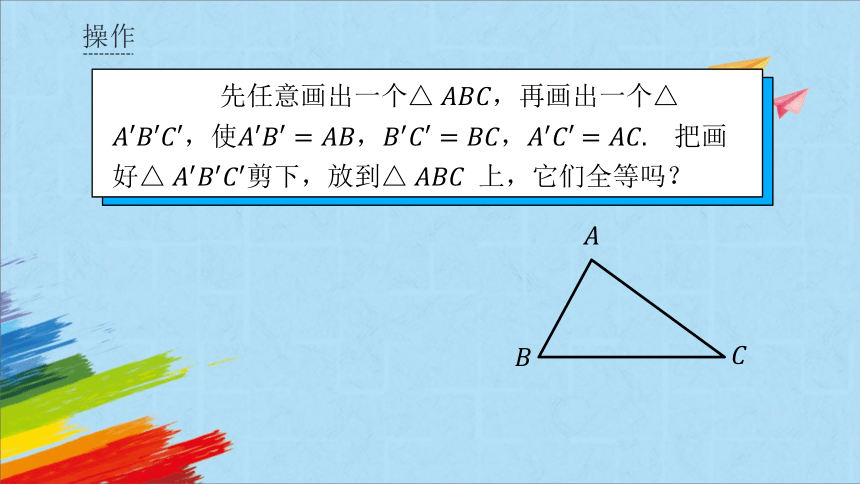
操作
先任意画出一个,再画出一个,使,, 把画好剪下,放到 上,它们全等吗?
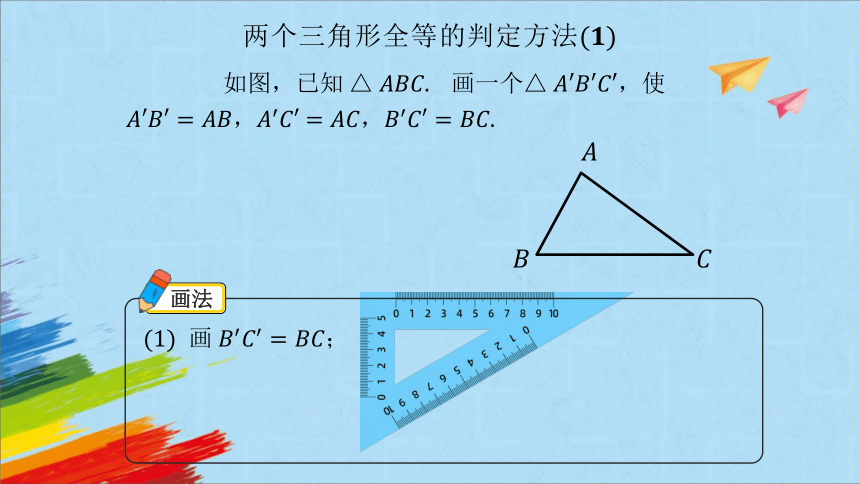
两个三角形全等的判定方法
画
如 画一个,使 ,
画法
两个三角形全等的判定方法
如 画一个,使 ,
画
画法
两个三角形全等的判定方法
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
如 画一个,使 ,
画
画法
两个三角形全等的判定方法
如 画一个,使 ,
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
画
画法
两个三角形全等的判定方法
如 画一个,使 ,
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
画
画法
画法
两个三角形全等的判定方法
连接,.
如 画一个,使 ,
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
画
画法
两个三角形全等的判定方法
如 画一个,使 ,
连接,.
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
画
两个三角形全等的判定方法
判定:
如 画一个,使 ,
现象
说明
两个三角形放在一起能完全重合.
这两个三角形全等.
条件
,,
“”判定方法:
三边对应相等的两个三角形全等.
(可简写成“边边边”或“”).
用符号语言表达:
在,
.
判断两个三角形全等的推理过程,叫做证明三角形全等.
我们在学习三角形时,提到“三角形具有稳定性”,它的含义是什么?你能用今天所学的知识解释这一性质吗?
三角形的稳定性是指,当三角形的三条边长确定后,三角形的形状大小也唯一确定.
依据 判定方法,若两个三角形三边对应相等,那么这两个三角形全等,从而它们的形状大小也是相同的. 因此给定三条边长后,只能画出形状大小唯一的三角形.
思考
如图,有一个三角形钢架, 是连接点与 中点 的支架. 求证:
分析
证明两个三角形全等,应该满足什么条件?
应该满足三条边分别相等.
例
如图,有一个三角形钢架, 是连接点与 中点 的支架. 求证:
例
的中点,
证明:
与,
.
用尺规作一个角等于已知角.
已知:.
例
已知:..
作一个角等于已知角
作法
以点 为圆心,任意长为半径画弧,分别交 , 于点;
画一条射线 ,以点 为圆心,长为半径画弧,交于点 ;
作法
以点 为圆心,任意长为半径画弧,分别交 , 于点;
已知:..
作一个角等于已知角
作一个角等于已知角
已知:..
作法
画一条射线 ,以点 为圆心,长为半径画弧,交于点 ;
以点 为圆心,任意长为半径画弧,分别交 , 于点;
已知:..
作一个角等于已知角
作法
画一条射线 ,以点 为圆心,长为半径画弧,交于点 ;
以点 为圆心,任意长为半径画弧,分别交 , 于点;
以点 为圆心, 长为半径画弧,与上一步中所画的弧相交于点;
过点 画射线,则.
画一条射线 ,以点 为圆心,长为半径画弧,交于点 ;
以点 为圆心,任意长为半径画弧,分别交 , 于点;
以点 为圆心, 长为半径画弧,与上一步中所画的弧相交于点;
作法
作一个角等于已知角
已知:..
为什么 呢?
思考
在刚才的作图过程中,有哪些线段是相等的?
.
.
为什么?
与,
理由:
为什么 呢?
思考
练习
工人师傅常用角尺平分一个任意角. 做法如下:
如图, 是一个任意角,在边 , 上分别取 移动角尺,使角尺两边相同的刻度分别与,重合. 过角尺顶点 的射线即是 的平分线. 为什么
分析
性质
理由
与,
.
.
课
堂
小
结
探索三角形全等的条件,其基本思路和方法是什么
当满足一个条件时,两个三角形一定全等吗
探究1
一条边相等
一个角相等
课
堂
小
结
探索三角形全等的条件,其基本思路和方法是什么
两条边相等
一条边及一个角分别相等
两个角相等
当满足两个条件时,两个三角形一定全等吗
探究2
逐次增加条件
分类讨论
作图验证
课
堂
小
结
“”判定方法指的是什么?有何作用?
判定:
三边对应相等的两个三角形全等.
判定两个三角形全等
性质
对应角相等
课后作业
添加一个条件,由“”可判定
在的基础上,求证: ∥.
三角形全等的判定-
形状、大小相同的图形放在一起能够完全重合,能够完全重合的两个图形叫做全等形.
如果, 那么它们的对应边相等,对应角相等.
全等三角形的性质
就能判定
全等三角形的判定
根据全等三角形的定义,如果满足三条边分别相等,三个角分别相等,即
对两个三角形来说,以下六个条件中至少要满足几个条件,才能确保两个三角形全等呢
思考
关于边的条件
关于角的条件
当满足一个条件时,两个三角形一定全等吗
探究
一条边相等
一个角相等
仅满足一个条件时,不能确保两个三角形全等.
结论
探究
当满足两个条件时,两个三角形一定全等吗
两条边相等
一条边及一个角分别相等
两个角相等
当满足两个条件时,也不能确保两个三角形全等.
结论
探究
当满足三个条件时,两个三角形一定全等吗
三个条件
1
2
3
一角
4
一边
操作
先任意画出一个,再画出一个,使,, 把画好剪下,放到 上,它们全等吗?
两个三角形全等的判定方法
画
如 画一个,使 ,
画法
两个三角形全等的判定方法
如 画一个,使 ,
画
画法
两个三角形全等的判定方法
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
如 画一个,使 ,
画
画法
两个三角形全等的判定方法
如 画一个,使 ,
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
画
画法
两个三角形全等的判定方法
如 画一个,使 ,
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
画
画法
画法
两个三角形全等的判定方法
连接,.
如 画一个,使 ,
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
画
画法
两个三角形全等的判定方法
如 画一个,使 ,
连接,.
分别以点, 为圆心,线段 , 长为半径画弧,两弧相交于点;
画
两个三角形全等的判定方法
判定:
如 画一个,使 ,
现象
说明
两个三角形放在一起能完全重合.
这两个三角形全等.
条件
,,
“”判定方法:
三边对应相等的两个三角形全等.
(可简写成“边边边”或“”).
用符号语言表达:
在,
.
判断两个三角形全等的推理过程,叫做证明三角形全等.
我们在学习三角形时,提到“三角形具有稳定性”,它的含义是什么?你能用今天所学的知识解释这一性质吗?
三角形的稳定性是指,当三角形的三条边长确定后,三角形的形状大小也唯一确定.
依据 判定方法,若两个三角形三边对应相等,那么这两个三角形全等,从而它们的形状大小也是相同的. 因此给定三条边长后,只能画出形状大小唯一的三角形.
思考
如图,有一个三角形钢架, 是连接点与 中点 的支架. 求证:
分析
证明两个三角形全等,应该满足什么条件?
应该满足三条边分别相等.
例
如图,有一个三角形钢架, 是连接点与 中点 的支架. 求证:
例
的中点,
证明:
与,
.
用尺规作一个角等于已知角.
已知:.
例
已知:..
作一个角等于已知角
作法
以点 为圆心,任意长为半径画弧,分别交 , 于点;
画一条射线 ,以点 为圆心,长为半径画弧,交于点 ;
作法
以点 为圆心,任意长为半径画弧,分别交 , 于点;
已知:..
作一个角等于已知角
作一个角等于已知角
已知:..
作法
画一条射线 ,以点 为圆心,长为半径画弧,交于点 ;
以点 为圆心,任意长为半径画弧,分别交 , 于点;
已知:..
作一个角等于已知角
作法
画一条射线 ,以点 为圆心,长为半径画弧,交于点 ;
以点 为圆心,任意长为半径画弧,分别交 , 于点;
以点 为圆心, 长为半径画弧,与上一步中所画的弧相交于点;
过点 画射线,则.
画一条射线 ,以点 为圆心,长为半径画弧,交于点 ;
以点 为圆心,任意长为半径画弧,分别交 , 于点;
以点 为圆心, 长为半径画弧,与上一步中所画的弧相交于点;
作法
作一个角等于已知角
已知:..
为什么 呢?
思考
在刚才的作图过程中,有哪些线段是相等的?
.
.
为什么?
与,
理由:
为什么 呢?
思考
练习
工人师傅常用角尺平分一个任意角. 做法如下:
如图, 是一个任意角,在边 , 上分别取 移动角尺,使角尺两边相同的刻度分别与,重合. 过角尺顶点 的射线即是 的平分线. 为什么
分析
性质
理由
与,
.
.
课
堂
小
结
探索三角形全等的条件,其基本思路和方法是什么
当满足一个条件时,两个三角形一定全等吗
探究1
一条边相等
一个角相等
课
堂
小
结
探索三角形全等的条件,其基本思路和方法是什么
两条边相等
一条边及一个角分别相等
两个角相等
当满足两个条件时,两个三角形一定全等吗
探究2
逐次增加条件
分类讨论
作图验证
课
堂
小
结
“”判定方法指的是什么?有何作用?
判定:
三边对应相等的两个三角形全等.
判定两个三角形全等
性质
对应角相等
课后作业
添加一个条件,由“”可判定
在的基础上,求证: ∥.
